前言

井字棋游戏，一个无法被人类玩家击败的程序

数字

皮亚诺公理

\begin{align} & \exists 0 \in \N \newline & \forall n \in \N , \exists n^, = succ(n) \in \N \newline & \forall n \in \N : n^, \neq 0 \newline & \forall n,m \in \N : n^ , =m^, \implies n=m \newline & \forall S \subset \N : (0 \in S \and \forall n \in S \implies n^, \in S) \implies S = \N \newline \end{align}

皮亚诺公理定义了何为自然数，同时定义了皮亚诺算术系统

加法公理

\begin{align} & a × 0 = 0 \newline & a + b^, = (a + b)^, \newline \end{align}

加法的交换律与结合律可以通过加法公理证明

乘法公理

\begin{align} & a + 0 = a \newline & a × b^, = a × b + a \newline \end{align}

乘法的交换律、结合律和分配律（左分配与右分配）可以通过加法公理和乘法公理证明

自然数的结构

我们可以这样定义自然数：

data Nat = zero | succ Nat

另外，我们定义叠加操作：

\begin{align} & foldn(z,f,0)=z \newline & foldn(z,f,n^,)=f(foldn(z,f,n)) \newline \end{align}

于是对于自然数，我们还可以这样表示：

n=foldn(zero,succ,n)

自然数的加法和和乘法可以分别被表示（这里采用了部分应用的思想）：

\begin{align} & (+m) = foldn(m,succ) \newline & (×m) = foldn(0,(+m)) \newline \end{align}

我们将 $foldn$ 中的 $n$ 视为序对，使用 Haskell 写点乏味的程序

foldn z _ 0 = z
foldn z f n = f (foldn z f (n - 1))

fib = fst . foldn (0, 1) h where
    h (m, n) = (n, m + n)

sum' = snd . foldn (0, 0) h where
    h (m, n) = (m + 1, m + 1 + n)

product' = snd . foldn (0, 1) h where
    h (m, n) = (m + 1, (m + 1) * n)

装载测试一下

*Main> fib 10
55
*Main> sum' 10
55
*Main> product' 10
3628800

自然数的同构

自然数不仅可以和自己的子集同构，例如奇偶数、平方数、斐波那契数，还可以和其他事物同构。其中一个例子是计算机程序中的数据结构——列表

下面是列表的定义：

data List A = nil | cons(A, List A)

这里的 cons 对应自然数中的 succ

同构于自然数的加法，定义列表的连接运算如下：

\begin{align} & nil + y = y \newline & cons(a,x) + y = cons(a, x+y) \newline \end{align}

可以利用递推公理证明列表连接的结合律，注意列表不满足交换律

我们同样可以定义列表的抽象叠加操作：

\begin{align} & foldr(c,h,nil)=c \newline & foldr(c,h,cons(a,x))=h(a,foldr(c,h,x)) \newline \end{align}

这里的 $h$ 是一个二元运算，foldr 表明这种这种操作是自右向左进行的

于是，我们可以把一个列表中的各个元素累加或累乘起来：

\begin{align} & sum=foldr(0,+) \newline & product=foldr(1,×) \newline \end{align}

将以上操作使用 Haskell 实现

foldr' :: (Num a) => a -> (a -> a -> a) -> [a] -> a
foldr' c h [] = c
foldr' c h (x:xs) = h x (foldr' c h xs)

sum' :: (Num a) => [a] -> a
sum' = foldr' (0) (+)

product' :: (Num a) => [a] -> a
product' = foldr' (1) (*)

重新定义列表的连接运算：

\begin{align} & (+y) = foldr(y,cons) \newline \end{align}

使用 Haskell 实现，这里需要注意 foldr 的类型发生了变化，为了通用化，调整了参数位置，其最终效果与 mappend 一致

foldr' :: (Num a) => (a -> [a] -> [a]) -> [a] -> [a] -> [a]
foldr' h [] c = c
foldr' h (x:xs) c = h x (foldr' h xs c)

append :: (Num a) => [a] -> [a] -> [a]
append = foldr' (:)

将一个列表的列表全部连接起来（相当于列表的乘法）：

\begin{align} & concat = foldr(nil,+) \newline \end{align}

使用 Haskell 实现，注意调整了类型与参数位置

foldr' :: (Num a) => ([a] -> [a] -> [a]) -> [a] -> [[a]] -> [a]
foldr' h c [] = c
foldr' h c (x:xs) = h x (foldr' h c xs)

concat' :: (Num a) => [[a]] -> [a]
concat' = foldr' mappend []

定义两个列表的重要操作，选择和逐一映射：

\begin{align} & map(f)=foldr(nil,cons \cdot first(f)) \newline & filter(p)=foldr(nil,(p \cdot 1st \mapsto cons,2nd)) \end{align}

使用 Haskell 实现，注意调整了类型

foldr' :: (Num a) => (a -> [a] -> [a]) -> [a] -> [a] -> [a]
foldr' h c [] = c
foldr' h c (x:xs) = h x (foldr' h c xs)

map' :: (Num a) => (a -> a) -> [a] -> [a]
map' f = foldr' h [] where
    h = \x -> \xs -> (:) (f x) xs

filter' :: (Num a) => (a -> Bool) -> [a] -> [a]
filter' f = foldr' h [] where
    h = \x -> \xs -> if (f x) then (:) x xs else xs

总结一下，调整类型是因为输入数据和输出数据的类型有变化，对应的函数类型也要思考处理，说明这里自定义的 foldr 并不通用（实际上这是对内置列表进行操作，而不是对定义的 List，更多细节参见第四章）

问题求解

最大子序和

foldr :: Foldable t => (a -> b -> b) -> b -> t a -> b

返回最大子序和，这里的 foldr 是内置函数

maxSum :: (Ord a, Num a) => [a] -> a
maxSum = fst . foldr f (0, 0) where
    f x (m, mSofar) = (m', mSofar') where
        mSofar' = max 0 (mSofar + x)
        m' = max mSofar' m

同时返回最大子序和和子序列

maxSumSequence :: (Ord a, Num a) => [a] -> (a, [a])
maxSumSequence = fst . foldr f ((0, []), (0, [])) where
    f x ((m, mList), (mSofar, mSofarList)) = (m', sofar') where
        sofar' = max (0, []) (x + mSofar, x : mSofarList)
        m' = max (m, mList) sofar'

这里需要注意变量的开头字母要小写，否则会被认为是值构造器，注意这里 m' 和 m 的类型并不相同（命名上的失误）

最长无重复字符子串

四元组的含义分别为：

已经找到的最长子串的长度
最长子串的右侧截止位置
当前正在检查的子串的右侧截止位置
记录各个不同字符上次出现位置的映射表格

import Data.Map as Map

longest :: String -> (Int, Int)
longest xs = fst2 $ Prelude.foldr f (0, n, n, Map.empty::(Map Char Int)) (zip [1..] xs) where
    fst2 (len, end, _, _) = (len, end)
    n = length xs
    f (i, x) (maxlen, maxend, end, pos) =
        (maxlen', maxend', end', Map.insert x i pos) where
            maxlen' = max maxlen (end' - i + 1)
            end' = case Map.lookup x pos of
                Nothing -> end
                Just j -> min end (j - 1)
            maxend' = if end' - i + 1 > maxlen then end' else maxend

在 fold 过程中维护一个已发现的最长无重复字符的子串，不断记录并检查遇到的字符 c 上次出现的位置。如果 c 未出现过，或者出现在当前正在检查的子串之前，则延长当前的子串，并和已发现的最长子串比较。否则，说明当前正在检查的子串含有重复字符，需要从上次重复字符出现的位置后开始接下来的检查。

第二种方法是利用素数。我们将每个不同的字符映射到一个素数上，对于任何一个字符串，我们可以计算出对应的乘积。这样，对于任何一个新字符，我们可以通过其对应的素数是否整除字符串对应的素数来判断是否在字符串中出现过。

矩阵快速幂

对数时间求斐波拉契数列，另见 SICP

递归

欧几里得算法

原始版本

def gcm(a, b):
    if a == b:
        return a
    elif a < b:
        return gcm(a, b - a)
    else:
        return gcm(a - b, b)


print(gcm(3, 6))
print(gcm(3, 4))

名称 gcm 是最大公度（greatest common measure）的简称

优化版本

def gcm(a, b):
    if b == 0:
        return a
    else:
        return gcm(b, a % b)


print(gcm(3, 6))
print(gcm(3, 4))

正确性证明

两个方向，这里略去证明

扩展欧几里得算法

所谓扩展欧几里得算法，就是除了求得两个量 $a$ , $b$ 的最大公度 $g$ 外，同时找到满足贝祖等式 $ax + by = g$ 的两个整数 $x$ 和 $y$ ，贝祖等式即裴蜀定理，这里略去正确性证明。

使用贝祖等式，我们可以推导出扩展欧几里得算法：

\begin{align} ax + by & = gcm(a,b) \newline & =gcm(b,r_0) \newline & =bx^,+r_0y^, \newline & =bx^,+(a-bq_0)y^, \newline & =ay^,+b(x^,-y^,q_0) \newline & =ay^,+b(x^,-y^,\lfloor a/b \rfloor) \newline \end{align}

其中利用了欧几里得算法中的等式 $a=bq_0+r_0$

使用 Haskell 求解

gcmex a 0 = (a, 1, 0)
gcmex a b = (g, y', x' - y' * (a `div` b)) where
    (g, x', y') = gcmex b (a `mod` b)

二元线性不定方程求解

使用扩展欧几里得算法给出二元线性不定方程 $ax+by=c$ 的整数解：具体来说，就是先求出最大公度 $g$ ，并判断 $g$ 是否整除 $c$ ，若不能，则无整数解。否则，将满足贝祖等式的 $x_0$ , $y_0$ ，扩大 $c/g$ 倍得到一组特解 $x_1$ , $y_1$ 。然后得到一般二元线性不定方程的通解 $x = x_1 - kb/g$ 和 $y = y_1 +ka/g$ 。

使用 Haskell 求解，这里用到了上面的 gcmex，solve 给出了一组特解，jars 给出了绝对值之和最小的一组解

import Data.List (minimumBy)
import Data.Function (on)

solve a b c
    | c `mod` g /= 0 = (0, 0, 0, 0)
    | otherwise = (x1, u, y1, v)
    where
        (g, x0, y0) = gcmex a b
        (x1, y1) = (x0 * c `div` g, y0 * c `div` g)
        (u, v) = (b `div` g, a `div` g)

jars a b c = (x, y) where
    (x1, u, y1, v) = solve a b c
    x = x1 - k * u
    y = y1 + k * v
    k = minimumBy (compare `on` (\i -> abs (x1 - i * u) + abs (y1 + i * v))) [-m..m]
    m = max (abs x1 `div` u) (abs y1 `div` v)

倒水趣题

这道题结合了扩展欧几里得算法和二元线性不定方程求解，原题见 OpenJudge - 3151:Pots，题意如下：

使用两个瓶子，记大瓶子为 A，小瓶子为 B，共有 6 种操作：

将大瓶子 A 装满水；
将小瓶子 B 装满水；
将大瓶子 A 中的水倒空；
将小瓶子 B 中的水倒空；
将大瓶子 A 中的水倒入小瓶子 B；
将小瓶子 B 中的水倒入大瓶子 A。

给定两个瓶子的容量，只用上述操作，判断是否可以得到给定体积的水。

import Data.Tuple (swap)
import Data.List (minimumBy)
import Data.Function (on)

gcmex a 0 = (a, 1, 0)
gcmex a b = (g, y', x' - y' * (a `div` b)) where
    (g, x', y') = gcmex b (a `mod` b)

solve a b c
    | c `mod` g /= 0 = (0, 0, 0, 0)
    | otherwise = (x1, u, y1, v)
    where
        (g, x0, y0) = gcmex a b
        (x1, y1) = (x0 * c `div` g, y0 * c `div` g)
        (u, v) = (b `div` g, a `div` g)

jars a b c = (x, y) where
    (x1, u, y1, v) = solve a b c
    x = x1 - k * u
    y = y1 + k * v
    k = minimumBy (compare `on` (\i -> abs (x1 - i * u) + abs (y1 + i * v))) [-m..m]
    m = max (abs x1 `div` u) (abs y1 `div` v)

water a b c =
    if x > 0
        then pour a x b y
        else map swap $ pour b y a x
        where (x, y) = jars a b c

pour a x b y =
    steps x y [(0, 0)]
    where
        steps 0 0 ps = reverse ps
        steps x y ps@((a', b'):_)
            | a' == 0 = steps (x - 1) y ((a, b'):ps)
            | b' == b = steps x (y + 1) ((a', 0):ps)
            | otherwise = steps x y ((max (a' + b' - b) 0, min (a' + b') b):ps)

利用上面的程序，可以得到倒水的操作序列，测试如下

*Main> water 9 4 6
[(0,0),(9,0),(5,4),(5,0),(1,4),(1,0),(0,1),(9,1),(6,4),(6,0)]

取模运算

将取模运算推广到实数，下面的实现是线性时间

def mod(a, b):
    while b < a:
        a = a - b
    return a


print(mod(5.1, 2.3))

优化为对数时间

def mod(a, b):
    if a <= b:
        return a
    elif a <= 2 * b:
        return a - b
    else:
        c = mod(a, 2 * b)
        if c <= b:
            return c
        else:
            return c - b


print(mod(5.1, 2.3))

这里利用了一个定理，其中 $r=a\ mod\ 2b$

a \ mod \ b= \begin{cases} r & r \le b \newline r-b & r > b \newline \end{cases}

$λ-calculus$

Lambda calculus - Wikipedia

语法

$λ-expression$

原子： $x$
抽象： $(λx.M)$
应用： $(M\ N)$

自由变量与约束变量

+\ x\ ((λx.+\ x\ 1)\ 2)

上面的这个例子中，外层的 $x$ 是自由变量，内层的 $x$ 是约束变量。

变换

$α$ -变换用于改变形参的名字；
$β$ -规约用于实现函数应用；
$η$ -规约用于去除多余的 $λ$ 抽象。

递归的定义

定义阶乘函数：

fact = n \mapsto if \ n=0\ then \ 1 \ else \ n×fact(n-1)

然而这并不是合法的 $λ-expression$ ，因为抽象只定义了匿名函数，上述的定义形如：

fact = n \mapsto (...fact...)

我们反向使用 $β$ -规约，得到：

fact = (f \mapsto (n \mapsto (...f...)))\ fact

进一步抽象为：

fact = H\ fact

其中 $H=(f \mapsto (n \mapsto (...f...)))$ ，我们引入一个函数 $Y$ ，它接受一个函数，然后返回这个函数的不动点：

Y\ H = H\ (Y\ H)

对比可知：

fact = Y\ H

对于 $Y$ 的实现，详见 Fixed-point combinator - Wikipedia

对称

群

半群、幺半群、群

半群：封闭性、结合律
幺半群：封闭性、结合律、单位元
群：封闭性、结合律、单位元、逆元

一些幺半群的例子

斜堆（skew heap）可以用上一章定义的二叉树来实现：

data SHeap A = nil | node (SHeap A, A, SHeap A)

可以看出，除了名称，斜堆的定义和二叉树完全一样。非空堆的最小元素在树的根节点中。

定义斜堆的归并运算如下：如果其中任一堆为空，则归并结果为另一个堆。非空情况下，我们比较根节点，选择较小的作为新的根。然后把含有较大元素的树合并到某一子树上。最后再把左右子树交换。

可以证明，所有斜堆组成的集合，在这一归并运算下构成一个幺半群。

配对堆（pairing heap）与多叉树也有类似的关系

同态与同构

f(a)\cdot f(b)=f(a\cdot b)

对称群与置换群

一个包含 $n$ 个元素的集合的全体置换作成的群叫做 $n$ 次对称群（symmetric group）。这个群用 $S_n$ 来表示。而 $S_n$ 的任意一个子群被称作置换群（permutation group）。

Cayley’s theorem

Every group G is isomorphic to a subgroup of the symmetric group acting on G.

轮换与对换

编程实现：置换与轮换的转换

一个可以表示成偶数个对换的乘积称为偶置换。

交错群（alternating group）是一个有限集合偶置换之群，它是对称群的子群，即置换群。

循环群

循环群（cyclic group），是指能由单个元素所生成的群。

有限循环群同构于整数同余加法群，无限循环群则同构于整数加法群。

每个循环群都是阿贝尔群。

子群

用群 $G$ 的子群 $H$ 定义元素的一种等价关系：

a\sim b \iff ab^{-1} \in H

这一等价关系所决定的类叫做子群 $H$ 的右陪集，类似可以定义左陪集。

由子群和陪集的性质，可以证明拉格朗日定理：

|H|\biggm| |G|

若左陪集等于右陪集，则子群 $H$ 被称为正规子群。我们可以把正规子群 $H$ 的所有陪集视为一个集合，并且定义这个集合上的乘法为：

(xH)(yH)=(xy)H

可以验证，正规子群的陪集在这个乘法下构成一个群，叫做商群，用 $G/H$ 表示。

结合同态与同构的概念，我们有同态基本定理：

素数相关

这里是从拉格朗日定理延伸出来的内容

费马小定理与欧拉定理

拉格朗日定理的直接结果

埃拉托斯特尼筛法

另见 SICP，流

费马素数检测

另见 SICP，模块化思想

快速幂取模

环、域

$(R,+,\cdot)$ 构成一个环，若：

$(R,+)$ 形成一个交换群
$(R,\cdot)$ 形成一个半群
乘法关于加法满足分配律

一个环的有三种附加条件：

乘法满足交换律（满足这个条件的环叫做交换环）
乘法单位元存在（有了单位元，自然也可以规定逆元，但是并非任何元素都逆元）
不存在零因子（即 $ab=0 \implies a=0 \or b=0$ ，这样的环满足消去律）

同时满足这三个附加条件的环有一个特殊名称，叫做整环

一个环果满足以下条件，则叫做除环：

至少包含一个不等于零的元
乘法单位元存在
每个不等于零的元都有一个逆元

一个交换除环叫做一个域。

伽罗瓦理论

扩域

考虑所有形如 $a + b\sqrt{2}$ 的数组成的集合，其中 $a,b\in \Q$ ，显然有理数是这一集合的子集。容易验证，任何两个这样的数做加、减、乘、除法都仍然可以写成 $a + b\sqrt{2}$ 的形式。于是这些数组成的集合构成一个域，记为 $Q[\sqrt{2}]$ 。这就引出了扩域的概念。

如果域 $E$ 包含域 $F$ ，我们称 $E$ 是 $F$ 的扩域，记作 $F \subseteq E$ 或者 $E/F$ 。

包含方程 $p(x) = 0$ 全部根的最小扩域叫做 $p(x)$ 的分裂域。也称为根域。

如果每次扩张所用的 $α_i$ 都是根式，我们称扩域 $F[α_1, α_2, ..., α_k]$ 为 $F$ 的根式扩域（radical extension）。

自同构

域上的自同构概念，将扩域和群联系了起来。

以 $Q[\sqrt{2}]$ 为例，定义一个从 $Q[\sqrt{2}]$ 到 $Q[\sqrt{2}]$ 的函数 $f$ ：

f(a + b\sqrt{2})=a - b\sqrt{2}

则 $f$ 就是一个域上的自同构。

域的自同构（Field Automorphism）是一个可逆函数 $f$ ，它将域映射到自身，并满足：

f(x+y)=f(x)+f(y),f(ax)=f(a)f(x),f(1/x)=1/f(x)

域的自同构背后的思想是，我们可以重新调换域中的元素，而完全不影响域的结构。

进一步，如果 $E$ 是 $F$ 的扩域，并且在域 $E$ 的自同构 $f$ 的基础上还满足一条额外的性质：对 $F$ 中的任何元素 $x$ 都有 $f(x) = x$ ，则称为 $E$ 上的 $F$ -自同构。

对于 $Q[\sqrt{2}]$ 这个例子，只有两个 $Q$ -自同构：一个是恒等变换 $g(x) = x$ ，另外一个就是我们前面定义的 $f$ 。

伽罗瓦群

如果把所有的自同构做成一个集合，这些自同构间的二元运算是复合变换，恒等变换是单位元，我们就得到了一个群。这个群被称作伽罗瓦群。

我们还是用 $p(x) = x^2 - 2$ 举例。伽罗瓦群 $G = Gal(p) = \{f,g\}$ ，包含两个元素，一个是 $f(a + b\sqrt{2})=a - b\sqrt{2}$ ，另一个是 $g(x) = x$ 。其中单位元是 $g$ 。可以验证 $f \cdot f=g$ 。

这说明 $G$ 的确是一个群，并且在同构的意义下等同于二阶循环群，它也同构于二阶对称群 $S_2$ 。

下面是伽罗瓦群的定义，对于 $F$ 的扩域 $E$ ，我们有一组 $E$ 的 $F$ -自同构的集合 $G$ 。对任意 $G$ 中的两个 $F$ -自同构 $f, g$ ，定义二元运算 $(f \cdot g)(x) = f(g(x))$ 。我们称 $G$ 为扩域 $E/F$ 的伽罗瓦群。记为 $Gal(E/F)$ 。

伽罗瓦基本定理

从方程系数所在的域 $F$ 开始，我们可以进行一系列扩域一直到达分裂域 $F \in F1 \in F2 ... \in E$ 。对应的伽罗瓦群为 $Gal(E/F)$ 。伽罗瓦发现，这个群的所有子群和这些中间域 $F_1, F_2, ...$ 之间存在着反序的一一对应。

我们举一个具体的例子。考虑方程 $x^4+8x^2+15 = 0$ ，它也可以表示成 $(x^2-3)(x^2-5) = 0$ 。它的系数域是有理数域 $\Q$ ，方程的分裂域是 $E = Q[\sqrt{3},\sqrt{5}]$ 。它的伽罗瓦群 $Gal(E/Q)$ 的阶是 4，同构于一个 4 阶循环群。可以找到 3 个中间扩域分别是 $Q[\sqrt{3}]$ ， $Q[\sqrt{5}]$ ， $Q[\sqrt{15}]$ ，这 3 个中间扩域对应的子群的阶都是 2。而方程的伽罗瓦群，也就是 4 阶循环群只有一个 2 阶子群。除此之外，它不再有其它非平凡子群了。

分裂域上的任意元可以写成如下形式：

\begin{align} & (a+b\sqrt{3})+(c+d\sqrt{3})\sqrt{5} \newline & = a+b\sqrt{3}+c\sqrt{5}+d\sqrt{15} \newline \end{align}

其中 $a,b,c,d\in \Q$ 我们定义如下自同构：

变换 $f$ 将 $\sqrt{3}$ 反号
变换 $g$ 将 $\sqrt{5}$ 反号
变换 $f\cdot g$ 将 $\sqrt{3}$ 和 $\sqrt{5}$ 反号

再加上恒等变换，基本域 $Q$ 上的伽罗瓦群一共有 4 个元素： $G = \{1, f, g, (f \cdot g)\}$ 。这个群同构于克莱因群，而克莱因群相当于是两个 2 阶循环群的积。它共有 5 个子群，每个都对应着一个扩域：

只含有单位元 $\{1\}$ 的子群，对应于分裂域 $Q[\sqrt{3},\sqrt{5}]$
二阶子群 $\{1,f\}$ ，对应于扩域 $Q[\sqrt{5}]$
二阶子群 $\{1,g\}$ ，对应于扩域 $Q[\sqrt{3}]$
二阶子群 $\{1,f\cdot g\}$ ，对应于扩域 $Q[\sqrt{15}]$
$G$ 自身，对应于有理数域 $\Q$

我们也可以把这个方程的伽罗瓦群写成置换群的形式： $\{(1), (12), (34), (12)(34)\}$

其中置换 $(1)$ 表示保持 4 个根都不变
$(1 2)$ 表示交换 $\pm\sqrt{3}$ 这两个根
$(3 4)$ 表示交换 $\pm\sqrt{5}$ 这两个根
$(1 2)(3 4)$ 表示同时交换这两对根

通过伽罗瓦基本定理，我们已经成功地将方程在域上的问题，转换为对称群的问题了。接下来要做的就是最后一击，通过群揭示可解性的本质。

可解性

为何从一元五次方程开始就没有由有限次加、减、乘、除、开方运算构成的求根公式了？

在一些限制条件下，任何根式扩域 $F[α_1, α_2, ..., α_k]$ 都组成一系列递增的链条：

F=F_0 \subseteq F_1 \subseteq ...\subseteq F_k = F[α_1, α_2, ..., α_k]

和这一系列扩域链对应的，是一系列递减的子群链：

Gal(F_k/F_0)=G_0 \supseteq G_1 \supseteq ... \supseteq G_k=Gal(F_k/F_k)=\{1\}

可以证明： $G_i$ 是前一个群 $G_{i-1}$ 的正规子群，而商群 $G_{i-1}/G_i$ 是阿贝尔群。

而对于一般的一元五次方程，对应的子群链是 $S_5 \supseteq A_5 \supseteq \{1\}$ ，但是 $A_5/\{1\}$ 不是阿贝尔群，因此它不是可解群。这样它对应的一般的一元五次方程不是根式可解的。（其中 $A_5$ 为 5 阶交错群）

另一种思路：

当 $n\ge5$ 时， $G_0$ 包含所有根的置换，同构于对称群 $S_n$ ，它必然包含 3 循环置换 $(a b c)$ 。

由数学归纳法可以证明，子群链条中所有的群都包含 3 循环置换。但这是不可能的，因为最后一个群是 $\{1\}$ ，它不含 3 循环置换。

详见：单群和交错群的单性

后记

说起群论，我想起了之前见过的魔群月光猜想，详见下面这个视频：

群论与 808017424794512875886459904961710757005754368000000000

Classification of finite simple groups - Wikipedia

这里对于伽罗瓦理论的介绍极其简略，关键的步骤均进行了删减，主要目的还是体现伽罗瓦理论的思想，毕竟这是抽象代数一个学期的内容，这么小的地方不可能面面俱到。

更多的内容准备去学习近世代数基础。

范畴

这一章看的有点懵，准备去看 Category Theory for Programmers 了，下面把一些支零破碎的内容写下来。

范畴

一组对象（object）和一组箭头（arrow），满足结合性公理和单位元公理。

一些例子：

集合和关系
群和态射
偏序集和单调函数

我们还可以从任何已知的范畴产生新的范畴，例如把一个范畴中的所有箭头反向就得到了一个对偶的范畴。

函子

函子（functor）就是用来对范畴及其内在的关系（对象和箭头）进行比较的。

在某种意义上说，函子好比是范畴之间的变换关系（态射）。但是它不仅把一个范畴中的对象映射为另一范畴中的对象，它还将一个范畴中的箭头映射到另一个范畴中。这一点是和普通的态射（例如群之间的态射）不同的。

函子必须满足两条性质：

函子必须保持恒等箭头仍然变换为恒等箭头
函子必须能够保持箭头的组合仍然变换为箭头的组合（covariance and contravariance）

和编程语言中的协变返回类型应该有关系

这便是 functor laws：

fmap id = id
fmap (f . g) = fmap f . fmap g

书上的例子都很熟悉，就不赘述了。

积和余积

这里的积是指范畴的积。为了容易理解，我们先从集合范畴入手：

集合的积是笛卡尔积
集合的余积是不相交的并集

在一些编程环境中，积可以通过二元组以及函数 fst 和 snd 来实现，余积可以通过 Either 数据类型来实现的。

积和余积的性质看不太懂，看这张图：

所谓二元函子，就是作用于两个范畴的积，积函子和余积函子只是二元函子的一个特例，以 Haskell 为例：

class Bifunctor f where
    bimap :: (a -> c) -> (b -> d) -> f a b -> f c d

instance Bifunctor (,) where
    bimap f g (x, y) = (f x, g y)

instance Bifunctor Either where
    bimap f _ (Left a) = Left (f a)
    bimap _ g (Right b) = Right (g b)

对于偏序集范畴，积是 $\and$ ，余积是 $\or$ 。

自然变换

可以说在范畴论中，箭头用于比较对象，而函子用于比较范畴。那么我们用什么比较函子呢？自然变换正是用于比较函子的工具。

这里略去自然变换的定义，举两个例子：

第一个例子是前缀枚举函数 inits。任给一个字符串或者列表，inits 可以枚举出所有的前缀：

inits :: [a] -> [[a]]
inits [] = [[]]
inits (x:xs) = (:) [] (map (\y -> (:) x y) (inits xs))

第二个例子叫做 safeHead，它的行为是安全地获取列表中的第一个元素。所谓“安全”，就是说它能够处理空列表的情况。

safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x:xs) = Just x

这里的类型变量没有类型限制，也就是说，这些都是多态函数（对所有对象进行抽象，这样就得到了一族箭头），于是一般的，自然变换可以这样写：

phi :: forall a . F a -> G a

通常我们不需要明确标明 forall a，这样自然变换就可以写为：

phi :: F a -> G a

关于 forall 关键词，参见 6.11.1. Explicit universal quantification (forall)

在函数式编程中，所有的多态函数都是自然映射

我们说自然变换是用来比较函子的。仿照抽象代数中同构的含义，我们需要定义什么情况下认为两个函子是“等价”的，也就是自然同构，这里也略去其定义。

初始对象和终止对象

在任意范畴 $C$ 中，如果有一个特殊的对象 $S$ ，使得范畴中的每个对象 $A$ 都有一个唯一的箭头，使得：

S \to A

称对象 $S$ 为初始对象，若反过来：

A \to S

称对象 $S$ 为终止对象。

初始对象和终止对象是对偶的，可以证明初始对象的同构唯一性，终止对象可以通过对偶性同理。

编程环境的类型系统本质上是集合范畴，在 Haskell 中，初始对象可以定义为：

data Void
absurd :: Void -> a
absurd _ = undefined

终止对象可以定义为：

data () = ()
unit :: a -> ()
unit _ = ()

集合范畴的例子中，我们说从终止对象到任何集合的箭头叫做选择箭头，它在编程中意味着什么呢？集合对应着类型，它表示我们可以从任何类型中选出特定的值，如：

zero :: () -> Int
zero () = 0
one :: () -> Int
one () = 1

幂对象

本质上，幂对象就是函数对象，如：

A×B\stackrel{g}{\longrightarrow}C

可以转换为：

A\stackrel{λg}{\longrightarrow}C^B

这便是柯里化的定义：

curry :: ((a, b) -> c) -> a -> b -> c
curry f x y = f (x, y)

uncurry :: (a -> b -> c) -> ((a, b) -> c)
uncurry f (x, y) = f x y

笛卡儿闭范畴

一个终止对象
任何一对对象都有积
任何一对对象都有幂

对象算术理论

Equational theory

Universal algebra

这一部分介绍了基本算术运算在一个笛卡尔闭的范畴上的对应，有点抽象。

由于编程环境的类型系统本质上是集合范畴，属于笛卡儿闭范畴，所以这里也说明了类型系统的本质。

多项式函子

以上介绍的在笛卡尔闭范畴上的算术主要是针对对象的。如果我们把函子考虑进来，会怎样呢？由于函子既作用于对象，也作用于箭头，这样就产生了多项式函子的概念。多项式函子是使用常函子、积函子和余积函子递归构造的：

恒等函子和常函子是多项式函子
若函子 $F$ 和 $G$ 是多项式函子，则它们的组合 $FG$ ，和 $F+G$ 与积 $F×G$ 也是多项式函子

F-algebra

这里非常难，为第一章中的各种 fold 函数提供了理论基础。我们以幺半群为例：

幺半群的两条公理可以描述为二元运算函数和单位元选择函数，定义：

\begin{align} m(x,y) &= x \oplus y \newline e() &= 1_M \newline \end{align}

这两种函数（也就是箭头）的类型分别为：

\begin{align} M×M &\to M \newline 1 &\to M \newline \end{align}

现在可以说，任何幺半群都可以用一个三元组 $(M,m,e)$ 来表示了。组成幺半群的所有箭头，也就是代表所有可能的 $m$ 和 $e$ 的箭头集合，是两种幂对象的积：

M^{M×M}×M^1=M^{M×M+1}

通过余积来表示这种关系就是 $α = e + m$ ，用多项式函子来表示就是 $\text{F}M =1 +M×M$ ，其中：

\text{F}M \stackrel{α}{\longrightarrow}M

我们称这样定义了一个幺半群的 F-algebra，为 $(M,α)$ 。

在 Haskell 中，可以这样表示一个 F-algebra，为 $(String,evals)$ ：

type Algebra f a = f a -> a

data MonoidF a = MEmptyF | MAppendF a a deriving (Show)

evals :: Algebra MonoidF String
evals MEmptyF = e ()
evals (MAppendF s1 s2) = m s1 s2

e :: () -> String
e () = ""

m :: String -> String -> String
m = (++)

递归与不动点

在第一章中，我们介绍了自然数和皮亚诺公理。并且介绍了和自然数同构的事物。实际上，我们可以把所有类似自然数的东西都用 F-algebra 描述。

根据皮亚诺公理，自然数的函子应当这样定义：

data NatF A = ZeroF | SuccF A

这个函子是一个多项式函子 $\text{NatF}A =1+A$ ，我们令 $\text{Nat}=\text{NatF(NatF(...))}$ ，可以得到：

data Nat = Zero | Succ Nat

这恰恰是我们在第一章定义的自然数类型。这是函子层面的递归， $\text{Nat}$ 是函子 $\text{NatF}$ 的不动点。

初始代数和向下态射

在 F-algebra 组成的范畴中，如果存在初始对象，则这一初始对象叫做初始代数。

这里看不太懂，大概意思是说，F-algebra 中若存在初始代数 $(I, i)$ ，则存在到任何其它代数 $(A, f)$ 的唯一态射。我们把从 $I$ 到 $A$ 的态射记为 $(f)$ ，使得下面的范畴图可交换：

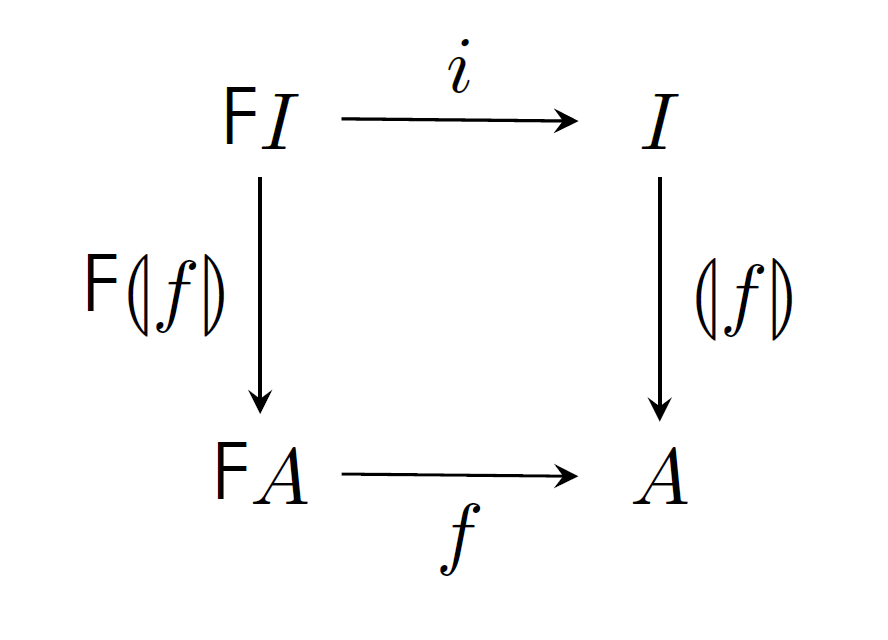
我们称箭头 $(f)$ 为向下态射。

向下态射的强大之处在于，它那能把一个非递归结构上的函数 $f$ ，转换为在递归结构上的函数 $(f)$ 。从而构造复杂的递归计算。我们仍然用自然数来举例子：

自然数函子 $\text{NatF}$ 是非递归的，而其初始代数自然数 $\text{Nat}$ 的定义是递归的：

data NatF A = ZeroF | SuccF A
data Nat = Zero | Succ Nat

所以箭头 $\text{NatF}A\stackrel{f}{\longrightarrow}A$ 是非递归的。一个 cata（向下态射）能够从 $f$ 构造出在递归的 $\text{Nat}$ 上进行计算的箭头 $\text{Nat}\to A$ 。所以 cata 的类型应为：

(\text{NatF}A\stackrel{f}{\longrightarrow}A) \stackrel{cata}{\longrightarrow} (\text{Nat}\to A)

我们可以根据这点定义出 cata 函数：

data NatF a = ZeroF | SuccF a

data Nat = Zero | Succ Nat

cata f Zero = f ZeroF
cata f (Succ n) = f (SuccF (cata f n))

这个自然数的向下态射对于任何携带对象都成立，它是非常通用的。我们进一步举两个具体的例子，第一个例子是将任何 $\text{Nat}$ 的值转换回 $\text{Int}$ ：

toInt :: Nat -> Int
toInt = cata eval where
    eval :: NatF Int -> Int
    eval ZeroF = 0
    eval (SuccF x) = x + 1

fromInt :: Int -> Nat
fromInt 0 = Zero
fromInt n = Succ (fromInt (n-1))

第二个例子关于斐波那契数列：

toFib :: Nat -> (Integer, Integer)
toFib = cata fibAlg where
    fibAlg :: NatF (Integer, Integer) -> (Integer, Integer)
    fibAlg ZeroF = (1, 1)
    fibAlg (SuccF (m, n)) = (n, m + n)

fibAt = fst . toFib . fromInt

事实上，对于任何满足皮亚诺公理的类自然数代数结构 $(A, c + f)$ ，我们都可以利用向下态射和初始代数 $(\text{Nat}, zero+succ)$ ，得到能够进行递归计算的 $(c+f)$ 。

可以证明，自然数上的向下态射 $(c+f)$ 正是 $foldn(c, f)$ 。

第一章中，我们是用归纳和抽象的方法得到了这个结论，现在，我们从更高的层面，把抽象的规律应用到具体的问题上得到了同样的结论。

代数数据类型

在第一章中，我们给出的列表定义为：

data List A = Nil | Cons A (List A)

而相应的非递归函子为：

data ListF A B = NilF | ConsF A B

可以验证 $\text{List}A$ 是函子 $\text{ListF}A$ 的不动点，于是列表 F-algebra 的初始代数为 $(\text{List}A,[nil,cons])$ 。

如果我们有一个非递归的计算 $f$ ，就可以利用向下态射构成针对递归列表的计算：

data List a = Nil | Cons a (List a)

data ListF a b = NilF | ConsF a b

cata :: (ListF a b -> b) -> (List a -> b)
cata f Nil = f NilF
cata f (Cons x xs) = f (ConsF x (cata f xs))

例如，可以定义计算列表长度的代数规则：

len :: (List a) -> Int
len = cata lenAlg where
    lenAlg :: ListF a Int -> Int
    lenAlg NilF = 0
    lenAlg (ConsF _ n) = n + 1

fromList :: [a] -> List a
fromList [] = Nil
fromList (x:xs) = Cons x (fromList xs)

通过改变代数规则 $f$ ，还可以得到其它针对列表的计算。下面的例子把列表中所有的元素累加起来：

sum :: (Num a) => (List a) -> a
sum = cata sumAlg where
    sumAlg :: (Num a) => ListF a a -> a
    sumAlg NilF = 0
    sumAlg (ConsF x y) = x + y

可以证明，列表 F-algebra 上的向下态射 $(c+f)$ 正是 $foldr(c, f)$ 。

注意这里的 foldr 与 Haskell 内置的 foldr 并不同

对于二叉树有着类似的结论。

后记

foldr :: Foldable t => (a -> b -> b) -> b -> t a -> b
foldMap :: (Foldable t, Monoid m) => (a -> m) -> t a -> m

我们来解读一段用范畴语言实现的通用叠加操作，通常我们认为列表的叠加操作可以这样写：

foldr f z [] = z
foldr f z (x:xs) = f x (foldr f z xs)

这让我们联想到幺半群，foldr 相当于在幺半群上重复进行二元操作。在抽象幺半群定义中，除了单位元和二元操作外，我们还可以定义将一列元素“累加”起来的操作。

对于任何幺半群 $M$ ，mconcat 可以将一个 $M$ 中元素的列表，通过二元运算和单位元叠加计算到一起。

现在我们可以对任何幺半群元素进行累加了。但能否让它变得更通用呢？如果有一列元素，它们虽然不是幺半群中的元素，但是如果我们能将它们转换为幺半群，就仍然可以进行累加。

将某一类型的列表映射为幺半群列表恰巧就是函子的行为。

可是美中不足的是，对于任何传入 foldr 的二元组合函数 $f : A \to B \to B$ ，如果 $B$ 不是幺半群，我们仍然无法进行叠加。现在考虑 $f$ 的克里化形式 $f : A \to (B \to B)$ ，我们发现以箭头 $B \to B$ 为对象，可以组成一个幺半群。其中单位元是恒等箭头 id，而二元运算是函数组合。为此，我们把这种 $B \to B$ 的箭头通过函子封装成一个类型，这便是自函子：

newtype Endo a = Endo { appEndo :: a -> a }

现在任给一个二元组合函数 $f$ ，我们都可以把它利用 foldMap 叠加到 Endo 幺半群上去了。最后一步我们使用 appEndo 取回结果。

foldr f z t = appEndo (foldMap (Endo . f) t) z

现在我们终于可以自信的说，单子说白了不过就是自函子范畴上的幺半群而已。

融合

本章中，我们用两个例子说明如何进行编程中的推导。

foldr / build fusion

列表的叠加操作

我们在第一章就给出过列表的叠加操作，它的定义为：

foldr f z [] = z
foldr f z (x:xs) = f x (foldr f z xs)

许多列表相关的操作都可以用叠加来定义，注意这里的 foldr 是内置的通用叠加操作，而非第一章那个连列表都难以通用的 foldr：

sum' :: (Num a) => [a] -> a
sum' = foldr (+) 0

and' :: [Bool] -> Bool
and' = foldr (&&) True

elem' :: (Eq a) => a -> [a] -> Bool
elem' x = foldr (\a -> \b -> (a == x) || b) False

map' :: (Num a) => (a -> a) -> [a] -> [a]
map' f = foldr (\a -> \b -> f a : b) []

filter' :: (Num a) => (a -> Bool) -> [a] -> [a]
filter' f = foldr (\a -> \b -> if f a then a : b else b) []

append' :: (Num a) => [a] -> [a] -> [a]
append' x y = foldr (:) y x

concat' :: (Num a) => [[a]] -> [a]
concat' = foldr append' []

叠加操作是如此基本（在上一章我们证明了叠加是列表的向下态射），如果我们能把列表的叠加操作的化简规律找到，就找到了所有列表操作的化简规律，而这便是 foldr / build fusion law。

foldr / build fusion law

现在我们考虑，如果把空列表 Nil 和连接操作 Cons 进行叠加会产生什么结果，我们得到了列表本身。换言之，如果我们有一个运算 $g$ ，它能够从一个起始值，例如 Nil，和一个二元组合运算，例如 Cons，产生一个列表。我们可以定义这个列表构造过程 build：

build(g) = g((:), [])

接着，如果用另一个起始值 $z$ 和二元组合运算 $f$ ，对这一列表进行叠加，其结果就相当于用 $z$ 替换 $[]$ ，用 $f$ 替换 $(:)$ ，然后直接调用过程 $g$ ：

foldr(f, z, build(g)) = g(f, z)

我们称这一结果为 foldr / build fusion law。

几个例子

在继续深入介绍前，让我们先看一些具体的例子。考虑如何计算从 $a$ 到 $b$ 间的整数，为此我们可以先产生从 $a$ 到 $b$ 之间的所有整数：

range(a,b)= \begin{cases} [] & a>b \newline a:range(a+1,b) & a\le b \newline \end{cases}

于是答案便是：

sum(range(a, b))

我们将其中的起始值和二元组合运算视为参数并柯里化：

range^,(a,b)=f \ c\mapsto \begin{cases} c & a>b \newline f\ a\ (range^,(a,b,f,c)) & a\le b \newline \end{cases}

这样原来的 $range$ 就可以用 $range^,$ 和 $build$ 表示了：

range(a, b) = build(range^,(a, b))

接下来我们用 foldr / build fusion law 化简累加和的计算：

\begin{align} sum(range(a,b)) & = sum(build(range^,(a, b))) \newline & =foldr((+),0,build(range^,(a, b))) \newline & =range^,(a,b,(+),0) \end{align}

这样就完成了化简，避免产生了中间列表，优化了算法，虽然这个例子可能并不明显。

另一个例子是把若干词语添加上空格，然后连接成句子。这样的文字处理过程通常叫做 join，简单起见，我们在句子最后也添上一个空格。一个典型的定义如下：

join' :: [String] -> String
join' ws = concat $ map (\w -> w ++ " ") ws

这个定义的性能不佳。在单词末尾添加空格是一个昂贵的计算，需要先移动到每个单词的末尾，然后再使用字符串连接操作。其次有多少单词，逐一映射就会产生多长的新列表。最后这些中间结果都被丢弃了。

可以使用 foldr / build fusion law 优化这一计算，优化的过程从略：

join' :: [String] -> String
join' ws = foldr (\w b -> foldr (:) (' ' : b) w) [] ws

由于 $concat \cdot map(f)$ 〸分常见，很多编程环境的标准库已经提供了这样的优化实现。

例如 Haskell 中的 concatMap，Java 和 Scala 中的 flatMap。

最后一个例子是快速排序，一个典型的算法如下：

qsort :: (Ord a) => [a] -> [a]
qsort [] = []
qsort (x:xs) = qsort (filter (\y -> y < x) xs) ++ [x] ++ qsort (filter (\y -> y >= x) xs)

通过同时处理两处 filter，并使用 foldr / build fusion law 优化 append 操作，可以重构成如下形式：

qsort :: (Ord a) => [a] -> [a]
qsort [] = []
qsort (x:xs) = foldr (:) (x : qsort bs) (qsort as) where
    (as, bs) = foldr h ([], []) xs
    h y (as', bs') = if y <= x then (y : as', bs') else (as', y : bs')

列表的构建形式

为了方便使用 foldr / build fusion law，我们可以把常见的能够产生新列表操作都写为 $build...foldr$ 的形式。这样当用叠加操作和这种形式的操作组合起来时， $foldr...(build...foldr)$ ，就可以使用融合律化简。

Prelude GHC.Base> :t build
build :: (forall b. (a -> b -> b) -> b -> b) -> [a]

首先是构造空列表：

Prelude GHC.Base> build (\f z -> z)
[]

接下来是产生新列表的一系列操作：

import GHC.Base

cons :: (Num a) => a -> [a] -> [a]
cons x xs = build (\f z -> f x (Prelude.foldr f z xs))

append' :: (Num a) => [a] -> [a] -> [a]
append' xs ys = build (\f z -> Prelude.foldr f (Prelude.foldr f z ys) xs)

concat' :: (Num a) => [[a]] -> [a]
concat' xss = build (\f z -> Prelude.foldr (\xs x -> Prelude.foldr f x xs) z xss)

map' :: (Num a) => (a -> a) -> [a] -> [a]
map' f xs = build (\g z -> Prelude.foldr (\y ys -> g (f y) ys) z xs)

filter' :: (Num a) => (a -> Bool) -> [a] -> [a]
filter' f xs = build (\g z -> Prelude.foldr (\x xs' -> if (f x) then g x xs' else xs') z xs)

可以通过 $build$ 的定义和 $β$ -规约验证这些定义。

有些编程环境，例如 Haskell 已经把 foldr / build fusion law 实现在编译器内部。这样只要我们把列表的常见操作用 $build...foldr$ 的形式定义好（Haskell 标准库已经用 $build...foldr$ 的形式现了大多数列表操作），机器就可以替代我们利用 foldr / build fusion law 进行化简，从而得到优化的程序，避免中间结果和多余的递归。

类型限制

对 $build(g)$ 中 $g$ 的类型作出限制：

g: \forall A.(\forall B.(A\to B\to B)\to B \to B)

由于里面有两个多态的类型 $A$ 和 $B$ ，因此它被称为二阶多态函数（rank-2 type polymorphic）。

shortcut fusion

人们发现 foldr / build fusion law 仅仅是众多种融合规则中的一个，现在这些规则统一被称为 shortcut fusion。它们在编译器优化，程序库优化中发挥了重要的作用。更多内容可参见 Correctness of short cut fusion。

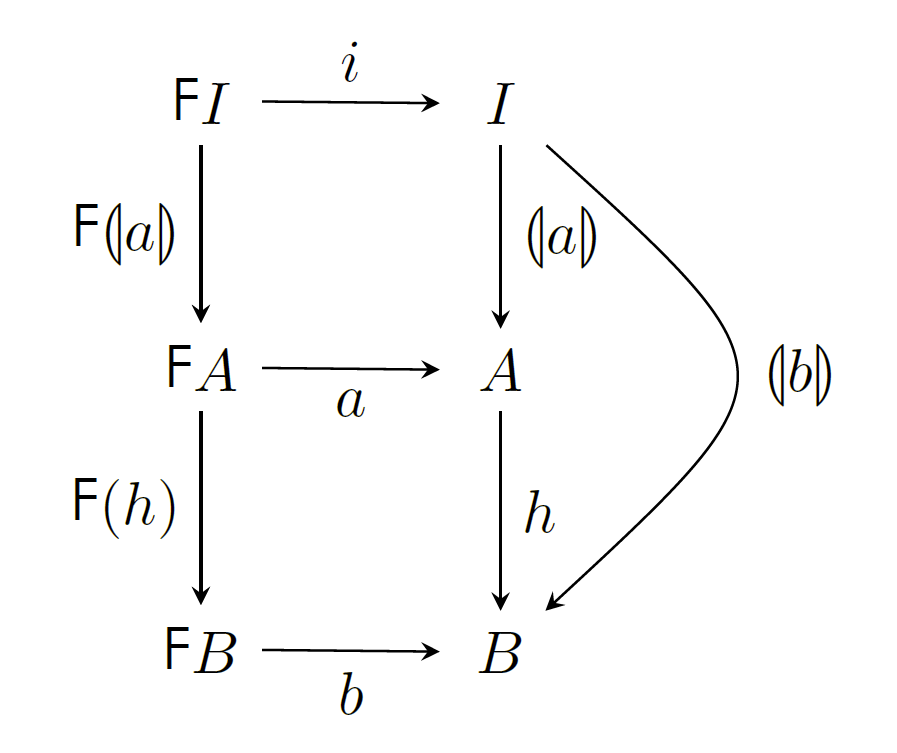
我们可以用范畴论推导出 foldr / build fusion law 及其推广的形式，核心是下面这张图，具体的推导过程从略：

Make a Century

把 $1$ 到 $9$ 这九个数字写成一行。只允许在这些数字之间添上加号和乘号，不许用括弧。如何使得最后的得数恰好是 $100$ ？

无穷

潜无穷

数组

int[] arr = new int[10];

动态容器

ArrayList<Integer> arrayList = new ArrayList<>();

链表

private class Node { // nested class to define nodes
    Item item;
    Node next;
}

惰性求值与无穷流

迭代

将列表的 $(:)$ 操作实现为惰性的，此处可参阅 SICP 的 delay 和 force。

然后定义 iter，这里的 iter 对应内置的 iterate 函数：

iter f x = x : iter f (f x)

利用内置的 take 函数（目前并不清楚如何实现惰性的 $(:)$ ，所以自定义的 take 没有用），可以从从潜无穷的流中取得给定个数的自然数：

nat = take 10 $ iter (+1) 0

乃至斐波拉契数：

fib = take 10 $ map fst $ iter (\(m, n)->(n, m + n)) (1, 1)
fib' = take 10 $ fst . unzip $ iter (\(m, n)->(n, m + n)) (1, 1)

也可以用叠加操作定义 iter：

iter' f x = x : foldr (\y ys -> f y : ys) [] (iter' f x)

递归

有些编程环境，所有的求值默认都是惰性的，在这样的环境中，我们甚至可以直接拿无穷流进行复杂的计算。

自然数：

nat = 0 : map (+1) nat

斐波拉契数：

fib = 1 : 1 : zipWith (+) fib (tail fib)

只含有 $2, 3, 5$ 这三个因子组成的自然数（另见 SICP）：

ham = 1 : map (*2) ham # map (*3) ham # map (*5) ham
    where
        xxs@(x:xs) # yys@(y:ys)
            | x==y = x : xs # ys
            | x<y = x : xs # yys
            | x>y = y : xxs # ys

余代数和无穷流

这里看不懂，不过和之前的 F-algebra 是对偶的（向上态射和终止代数），直接看例子吧：

data StreamF e a = StreamF e a
data Stream e = Stream e (Stream e)

ana :: (a -> StreamF e a) -> (a -> Stream e)
ana f = fix . f where
    fix (StreamF e a) = Stream e (ana f a)

takeStream 0 _ = []
takeStream n (Stream e s) = e : takeStream (n - 1) s

era (p:ns) = StreamF p (filter (p `notdiv`) ns)
    where notdiv p n = n `mod` p /= 0
primes = ana era [2..]

fib (m, n) = StreamF m (n, m + n)
fibs = ana fib (1, 1)

showPrimes = takeStream 15 primes
showFibs = takeStream 15 fibs

特别地，对于列表的向上态射被称为展开（反折叠 unfold）。向上态射和向下态射是互逆的。我们可以用向下态射把无穷流重新转换为列表。

实无穷

数的构造

\N \to \Z \to \Q \to \R

Equivalence Relation
Dedekind Cut

详见 5-relation-handout

超限数

序数和基数，详见信计导

悖论

计算的边界

停机问题

罗素悖论

自指

数学基础的分歧

逻辑主义：分支类型论
直觉主义：坚持要求可构造性，否定无限制地使用排中律，尤其在涉及无穷时
形式主义：形式化的数学系统，一致且完备
公理集合论：力图避免矛盾

哥德尔不完全性定理

第一不完全性定理
- 它表明，一致的形式化系统是不完备的。只要系统强大到足以包含自然数公理系统，都会有超越于它的问题。
第二不完全性定理
- 它表明，如果一个足以包含自然数算术的公理系统是一致的，那么这种一致性在该系统内是不可证明的。

Isomorphism - Mathematics of Programming

TOC

前言

数字