现代计算机图形学入门

Posted on:2022.04.04

TOC

Open TOC

Info

https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html

https://www.bilibili.com/video/av90798049

计算机图形学概述

课程概述

Gold standard in Video Games (Real-time Applications)

Gold standard in Animations / Movies (Offline Applications)

a8237a447cf74d0eb8f5271fb3923938.png

计算机图形学和计算机视觉

No clear boundaries.

839a786f30ae46dd8ece97cb444d7568.png

向量与线性代数

内积

Forward / backward (dot product positive / negative)

外积

Left / right (cross product outward / inward)

右手系

标准正交基

ea8b3982a8b241da87fd346c6f7a91dd.png

矩阵

cdaf2e666d654883945e343594021a25.png

变换（二维与三维）

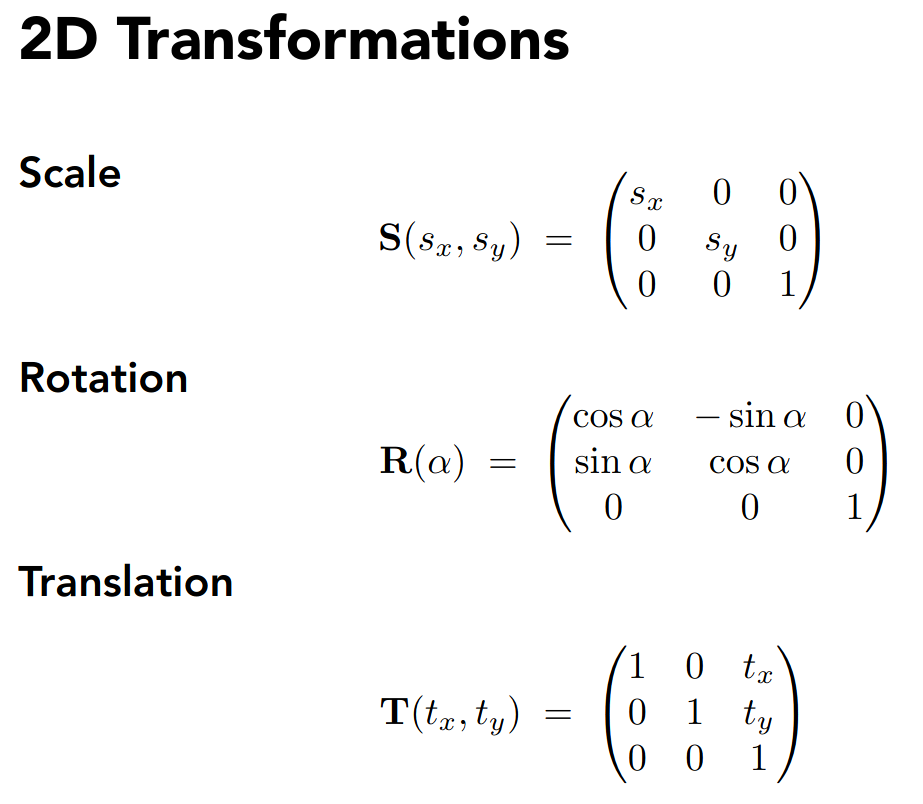
2D transformations

Homogeneous coordinates

注意到平移不是线性变换

于是引入齐次坐标形式，添加第三个分量

对于 point 而言

(x,y,1)(x,y,1)

对于 vector 而言

(x,y,0)(x,y,0)

基本的运算如下

d8e5b02c76684b99bc96f1073da78bb0.png

保持了相当的几何意义

注意 point 加上 point 定义为两个 point 的中点

于是对于仿射变换，可以统一为线性变换的形式

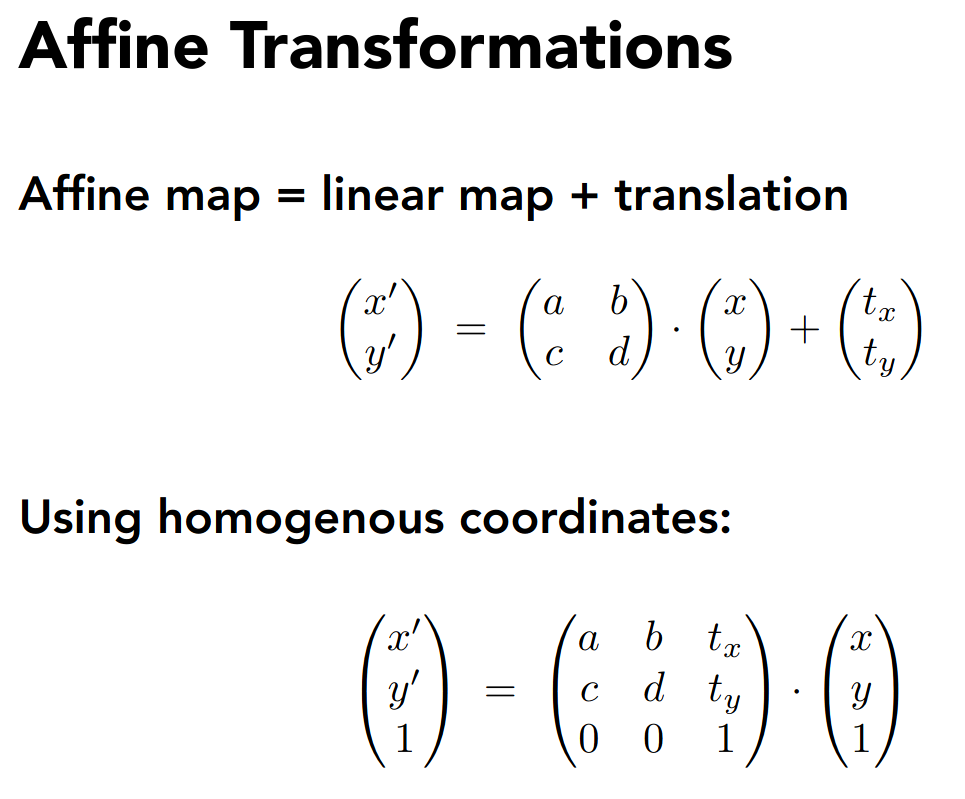
5797fde76cf649fdbcec0d19b4c3a193.png

注意是先做线性变换，再做平移

于是统一了平移和线性变换

ed2097ae8b33403b9c070705d9b40819.png

对于 3D Transformations，可以类似的推广

PA0

eigen

https://eigen.tuxfamily.org/index.php?title=Main_Page

sudo apt-get install libeigen3-dev

cmake

使用现代 cmake

cmake_minimum_required(VERSION 3.22.0)
project(Transformation)


add_executable(Transformation main.cpp)


find_package(Eigen3 REQUIRED)
target_include_directories(Transformation PUBLIC EIGEN3_INCLUDE_DIR)

target_link_libraries 似乎不必要

构建脚本 run.sh

Terminal window
rm -rf build
cmake -B build -DCMAKE_BUILD_TYPE=Debug -GNinja
cmake --build build --target Transformation
build/Transformation

note

简单的翻译一下即可

int main() {
  const double pi = std::acos(-1);


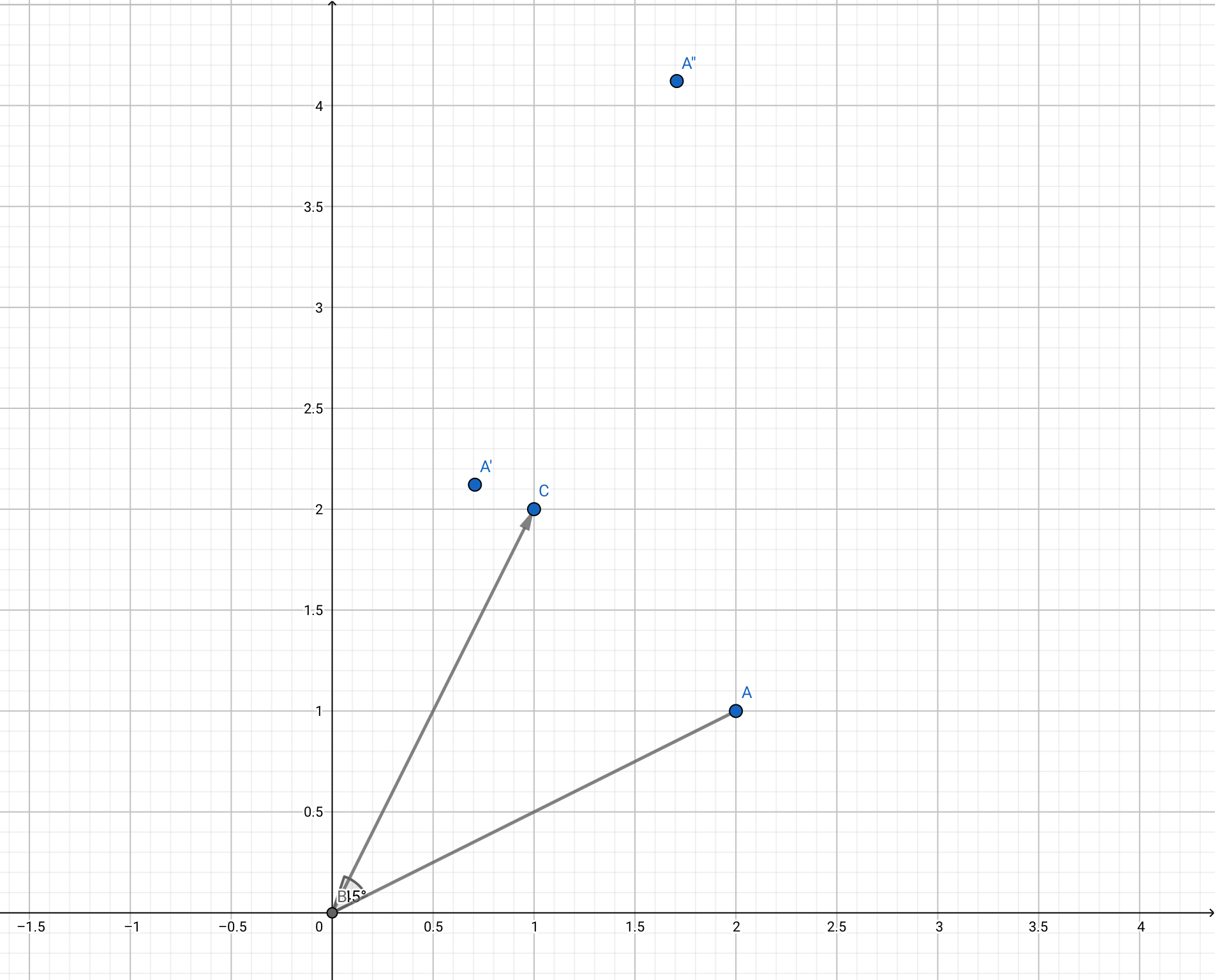
  Eigen::Vector3f vec(2.0f, 1.0f, 1.0f);
  Eigen::Matrix3f matrix;
  matrix << std::cos(pi / 4), -std::sin(pi / 4), 1.0f, std::sin(pi / 4),
      std::cos(pi / 4), 2.0f, 0.0f, 0.0f, 1.0f;


  std::cout << matrix * vec << std::endl;
  return 0;
}

输出为

1.70711
4.12132
      1

简单的验证一下

8c995a7ba24a40838d9b869dc49a47bf.png

变换（模型、视图、投影）

3D Transformations

对于三维变换，有类似的齐次坐标形式

缩放和平移都十分 easy，下面考虑旋转

由于旋转的自由度变大了，先考虑简单的情形，即绕坐标轴旋转

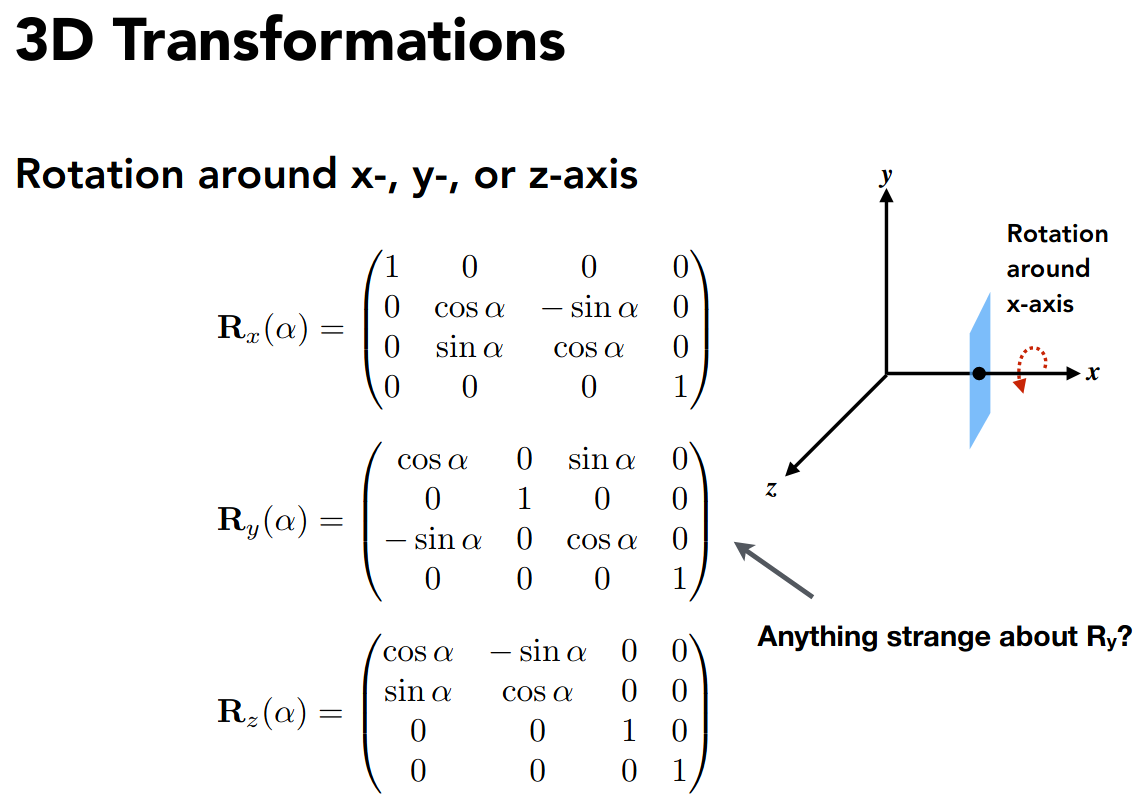
606fd5a5161a448d867cb101ff42cc35.png

注意到

x⃗×y⃗=z⃗x⃗×z⃗=−y⃗y⃗×z⃗=x⃗\begin{array}{l} \vec{x} \times \vec{y} = \vec{z} \newline \vec{x} \times \vec{z} = -\vec{y} \newline \vec{y} \times \vec{z} = \vec{x} \newline \end{array}

所以绕 y 轴旋转的矩阵有所不同

有了这三个矩阵，就可以描述三维空间中任意的旋转，这便是欧拉角

详见

另外还有一个公式叫罗德里格旋转公式

详见

Viewing transformation

想象在拍照片

  1. Find a good place and arrange people. (model transformation)
  2. Find a good angle to put the camera. (view transformation)
  3. Cheese! (projection transformation)

主要介绍后两种变换

View transformation

主要是摆放相机的位置

首先需要描述相机的位置

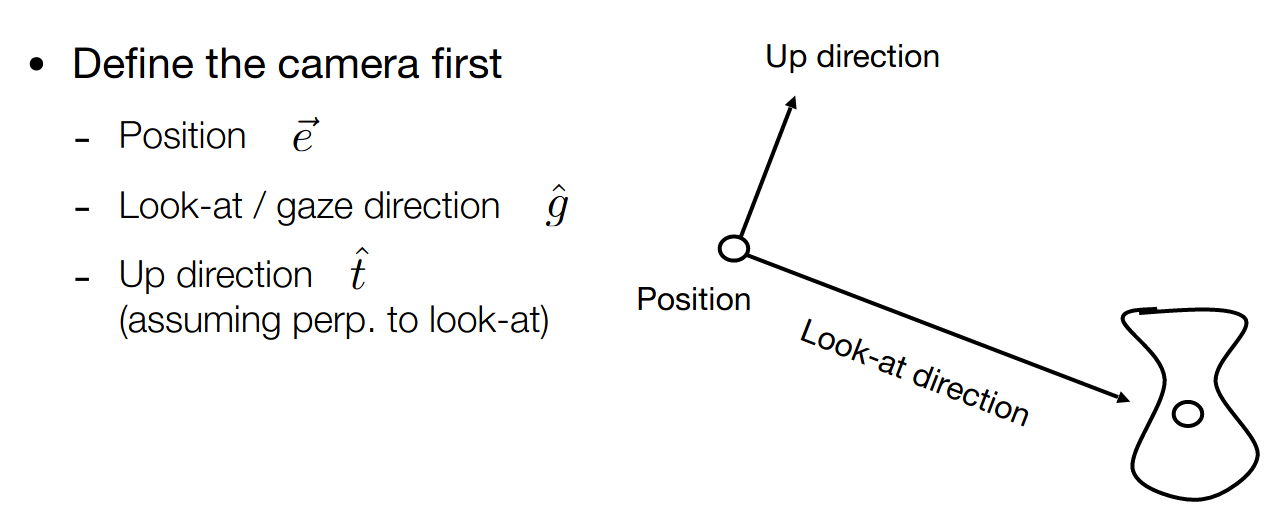
f7141b48c1ab40fd9b9bfc622dbcd03a.png

注意到物体和相机的相对位置

我们简化为，相机位于原点，头顶 y 轴，朝向 -z 轴，即

e⃗={0,0,0}g^={0,0,−1}t^={0,1,0}\begin{array}{l} \vec{e} = \{0,0,0\} \newline \hat{g} = \{0,0,-1\} \newline \hat{t} = \{0,1,0\} \newline \end{array}

下面考虑如何将相机变换到这个位置，这样物体只要使用相同的变换，就能保证相对位置不变

71b764c97f444eea9027cec7cb58674e.png

先做平移，再做旋转

第二步的关键在于，旋转变换矩阵是正交矩阵，即

MT=M−1M^{T} = M^{-1}

所以可以考虑逆变换，即将坐标轴旋转到相应的位置

Projection transformation

分为正交投影和透视投影

Orthographic Projection

We want to map a cuboid [l, r] x [b, t] x [f, n] to the canonical cube

left, right, bottom, top, far, near

由于相机朝向 -z 轴，所以 far 的 z 坐标更小

单位立方体就是

[−1,1]3[-1,1]^{3}

变换矩阵不难得到

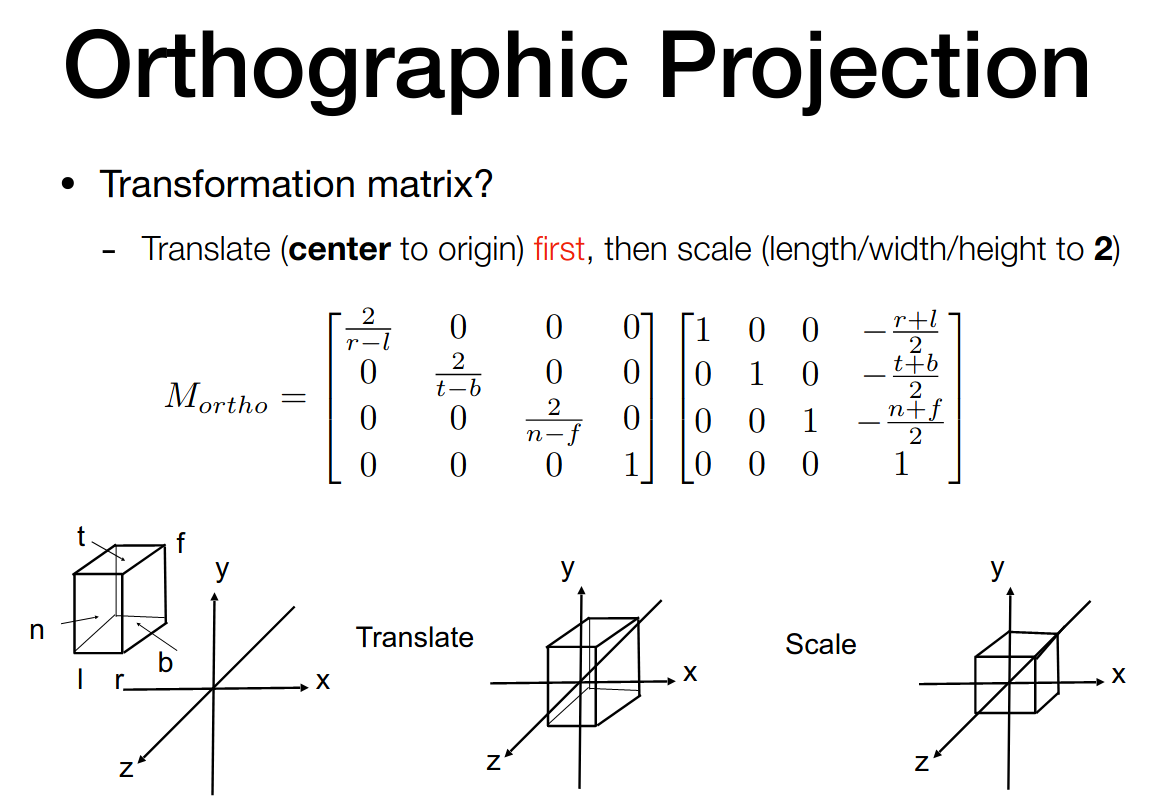
d08e797e4587464a81aac6189d4515b3.png

Perspective Projection

使用化归的思想，先将台体变换为长方体，再使用正交投影

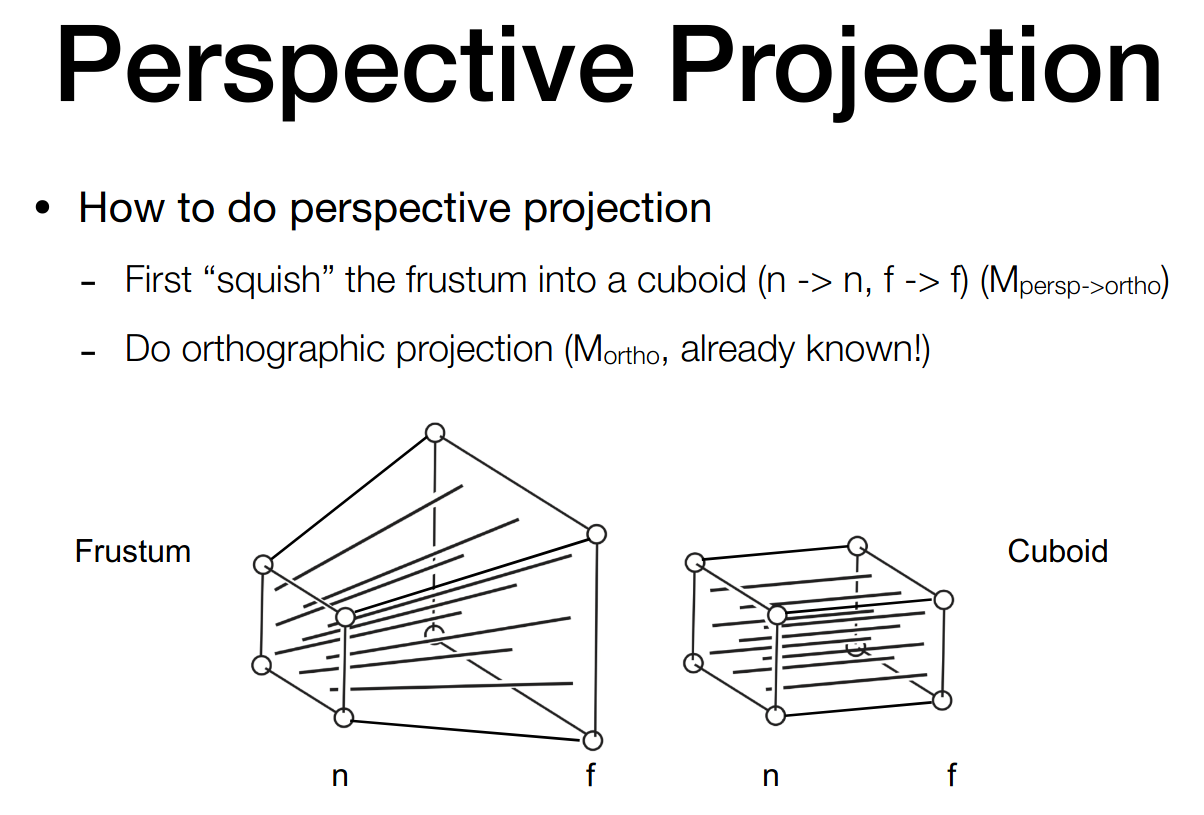
5df98c4fda614cfc871365f5dc35f35b.png

这里有一些假设

根据相似三角形关系，可以得到 x 分量和 y 分量的变换关系

y′=nzyx′=nzx\begin{array}{l} y' = \frac{n}{z} y \newline x' = \frac{n}{z} x \newline \end{array}

于是有

M⋅[xyz1]=[nynx?z]M \cdot \begin{bmatrix} x \newline y \newline z \newline 1 \end{bmatrix} = \begin{bmatrix} ny \newline nx \newline ? \newline z \end{bmatrix}

注意对齐次坐标中的 point 各分量数乘某个非零值并不改变 point

可以不严谨的得到

M=[n0000n00????0010]M = \begin{bmatrix} n & 0 & 0 & 0 \newline 0 & n & 0 & 0 \newline ? & ? & ? & ? \newline 0 & 0 & 1 & 0 \end{bmatrix}

下面根据假设，取 near 平面上的某点，在变换后不变，即

M⋅[xyn1]=[nynxn2n]M \cdot \begin{bmatrix} x \newline y \newline n \newline 1 \end{bmatrix} = \begin{bmatrix} ny \newline nx \newline n^{2} \newline n \end{bmatrix}

取 far 平面的中心点，在变换后不变，即

M⋅[00f1]=[00f2f]M \cdot \begin{bmatrix} 0 \newline 0 \newline f \newline 1 \end{bmatrix} = \begin{bmatrix} 0 \newline 0 \newline f^{2} \newline f \end{bmatrix}

综合诸式，可以不严谨的得到

M=[n0000n0000n+f−nf0010]M = \begin{bmatrix} n & 0 & 0 & 0 \newline 0 & n & 0 & 0 \newline 0 & 0 & n + f & -nf \newline 0 & 0 & 1 & 0 \end{bmatrix}

再左乘正交投影的矩阵即可

**思考题：**对于 near 平面和 far 平面的中间平面，考虑其中心点

M⋅[00n+f21]=[00n2+f2n+f1]M \cdot \begin{bmatrix} 0 \newline 0 \newline \frac{n + f}{2} \newline 1 \end{bmatrix} = \begin{bmatrix} 0 \newline 0 \newline \frac{n^{2}+f^{2}}{n+f} \newline 1 \end{bmatrix}

注意到

n+f2≤n2+f2n+f\frac{n + f}{2} \le \frac{n^{2}+f^{2}}{n+f}

所以实际上会变远

光栅化（三角形的离散化）

Viewport transformation

接着上节课的内容

当得到了一个单位立方体后，我们需要将其绘制在屏幕上

为简化考虑，我们忽略 z 分量，并做如下的变换

[−1,1]2→[0,width]×[0,height][-1,1]^{2} \to [0, \text{width}] \times [0, \text{height}]

这里的 width 和 height 是屏幕的参数

0533fbe553a64dc890c82c52b2d6fcad.png

更具体的，屏幕实际上是像素的二维数组

而光栅化表示在屏幕上绘制像素

目前我们使用 RGB 表示像素

下面定义 screen space

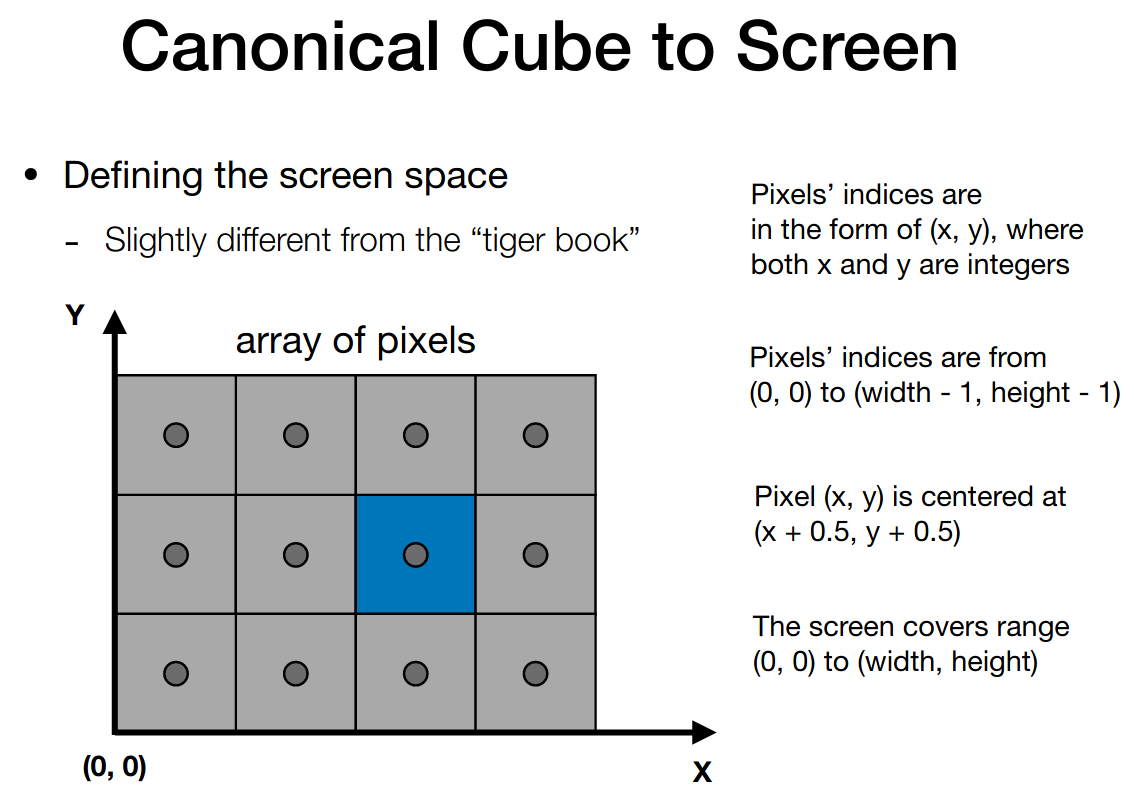
91423f2adc2f4c0680ff615b00b4e00c.png

注意区分像素和像素的下标

如此，Viewport transform matrix 易得如下

M=[width200width20height20height200100001]M = \begin{bmatrix} \frac{\text{width}}{2} & 0 & 0 & \frac{\text{width}}{2} \newline 0 & \frac{\text{height}}{2} & 0 & \frac{\text{height}}{2} \newline 0 & 0 & 1 & 0 \newline 0 & 0 & 0 & 1 \end{bmatrix}

Rasterization

Different raster displays

略

Rasterizing a triangle

绘制的基本单元为三角形，理由如下

71bbcef64a5c4dafac9122af51518c98.png

当我们得到三角形的三个顶点的坐标后，需要以像素的形式绘制出来

最基本的想法是——采样

使用一个二重循环即可

for (int x = 0; x < xmax; ++x)
  for (int y = 0; y < ymax; ++y)
    image[x][y] = inside(tri, x + 0.5, y + 0.5);

注意像素的中心需要加上 0.5

而 inside 函数用来判断该像素是否在三角形内部

显然，我们需要使用外积

当下面三个式子同向时

AB⃗×AP⃗BC⃗×BP⃗CA⃗×CP⃗\begin{array}{l} \vec{AB} \times \vec{AP} \newline \vec{BC} \times \vec{BP} \newline \vec{CA} \times \vec{CP} \newline \end{array}

P 点就在三角形内部

一些其他议题：

PA1

opencv

sudo apt install libopencv-dev python3-opencv

run

可以直接 ./run.sh，按 ESC 退出

也可以指定参数

./build/Rasterizer -r 20 pa1.png
mv pa1.png ~/Desktop/virtual-machine-repository/post/games101.assets/

note

两个函数的实现是简单的

Eigen::Matrix4f get_model_matrix(float rotation_angle) {
  Eigen::Matrix4f model = Eigen::Matrix4f::Identity();


  // TODO: Implement this function
  // Create the model matrix for rotating the triangle around the Z axis.
  // Then return it.
  float radian = rotation_angle / 180 * MY_PI;


  Eigen::Matrix4f translate;
  translate << std::cos(radian), -std::sin(radian), 0, 0, std::sin(radian),
      std::cos(radian), 0, 0, 0, 0, 1, 0, 0, 0, 0, 1;


  model = translate * model;


  return model;
}


Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar) {
  Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();


  // TODO: Implement this function
  // Create the projection matrix for the given parameters.
  // Then return it.
  float yTop = std::abs(zNear) * std::tan(eye_fov / 360 * MY_PI);
  float xRight = yTop * aspect_ratio;


  Eigen::Matrix4f ortho;
  ortho << 1 / xRight, 0, 0, 0, 0, 1 / yTop, 0, 0, 0, 0,
      2 / std::abs(zFar - zNear), 0, 0, 0, 0, 1;
  Eigen::Matrix4f persp;
  persp << zNear, 0, 0, 0, 0, zNear, 0, 0, 0, 0, zNear + zFar, -zNear * zFar, 0,
      0, 1, 0;


  projection = ortho * persp * projection;


  return projection;
}

提高项需要使用罗德里格旋转公式，就不做了

先分析一下三个变换矩阵

实际上就是绕 z 轴旋转

通过命令行指定 angle

也可以通过按 A 键与 D 键动态的变换 angle

实际上就是移动相机的位置

使用 eye_pos 描述

Eigen::Vector3f eye_pos = {0, 0, 5};

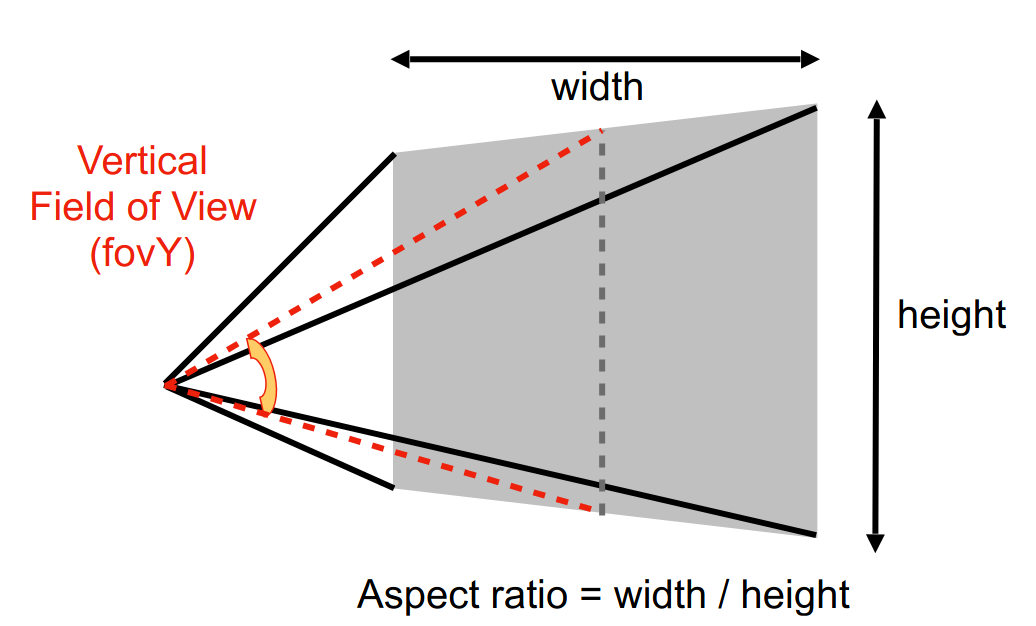
给出了 field-of-view (fov) 和 aspect ratio

有如下的关系

tanfov2=t∣n∣aspect ratio=rt\begin{array}{l} \text{tan} \frac{\text{fov}}{2} = \frac{t}{\lvert n \rvert} \newline \text{aspect ratio} = \frac{r}{t} \newline \end{array}

进而得到 left, right, bottom, top, far, near

需注意这里假定了对称性 l = -r, b = -t

然后先透视再正交投影即可

pic

修正透视投影矩阵后

dbf65036a6ef4362a63248fe30794b34.png

光栅化（深度测试与抗锯齿）

这一讲主要分析和处理 Aliasing Artifacts 问题

当采样频率低于实际信号的频率时，就会出现 Aliasing Artifacts

而一种解决方案就是进行 Pre-Filter 后，再进行 Sample

注意顺序

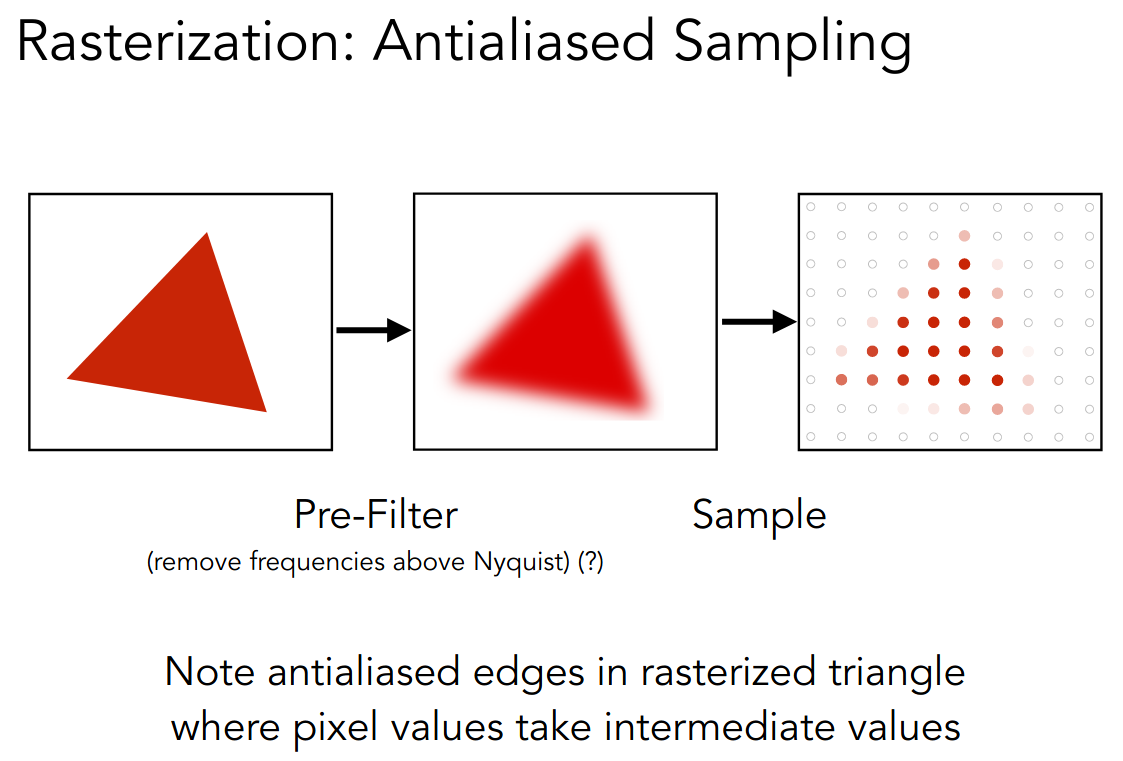
0491dc5ab76c4a2aa99a8f7d6a6c7529.png

下面解释

  1. Why undersampling introduces aliasing?
  2. Why pre-filtering then sampling can do antialiasing?

Why undersampling introduces aliasing?

从 spatial domain 和 frequency domain 两个角度来理解

祭出傅里叶变换

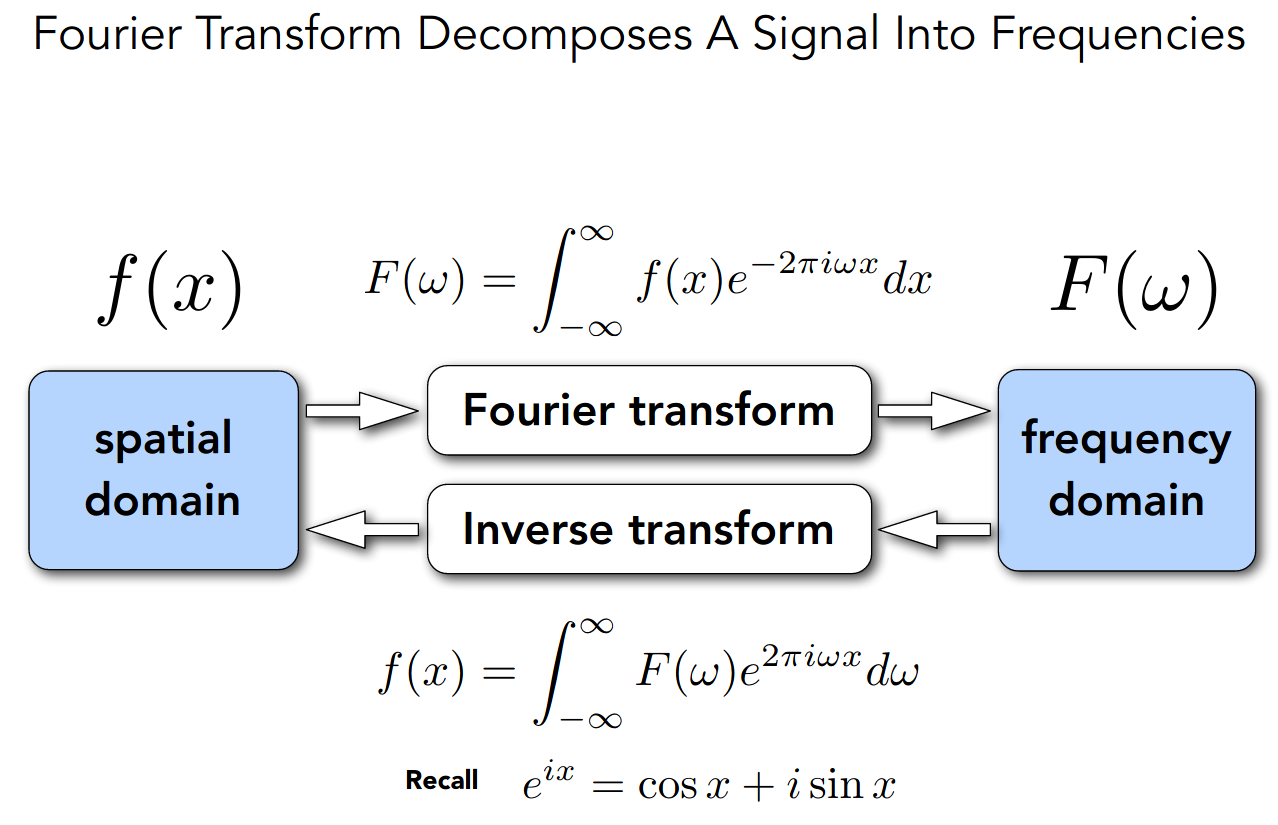
543a7b0ad2a74eaabda8e4c664ff598d.png

从 spatial domain 来理解

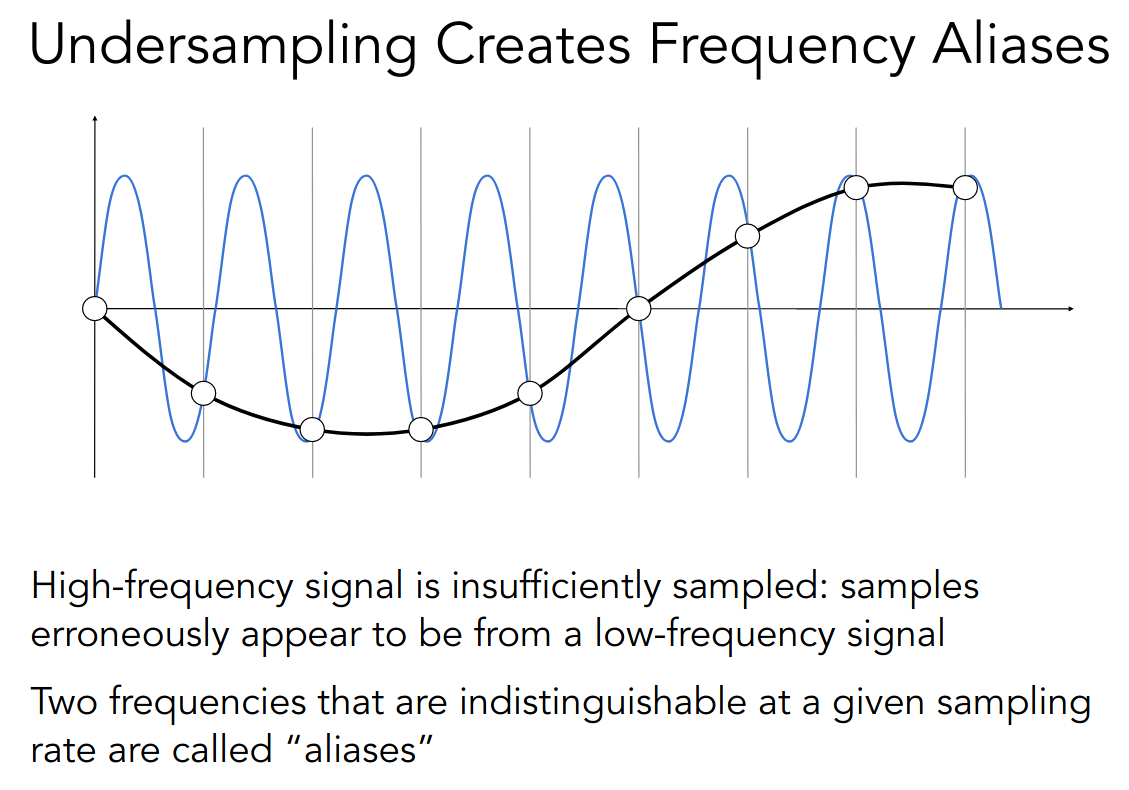
91f915adc4e94d3b92be60e285602fa2.png

从 frequency domain 来理解

这里似乎有关系，采样频率越低，在 spatial domain 间隔越大，在 frequency domain 间隔越小

具体见课件，反正不太懂

Why pre-filtering then sampling can do antialiasing?

在无法提升采样频率的前提下，使用低通滤波器过滤高频信息，可以避免 Mixed Frequency Contents

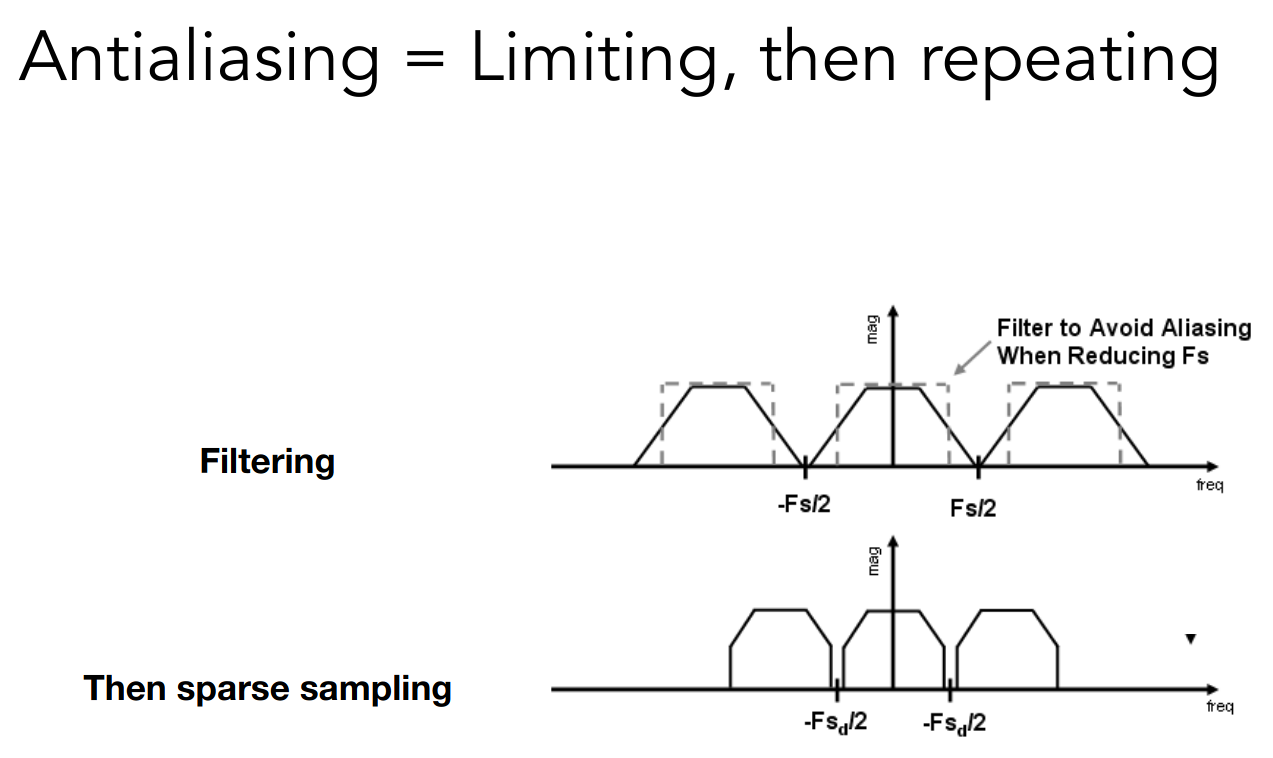
bca0e51b4f074efa848bd061b3c50918.png

而过滤，在 spatial domain 中就是卷积，就是取平均值，在 frequency domain 中就是相乘

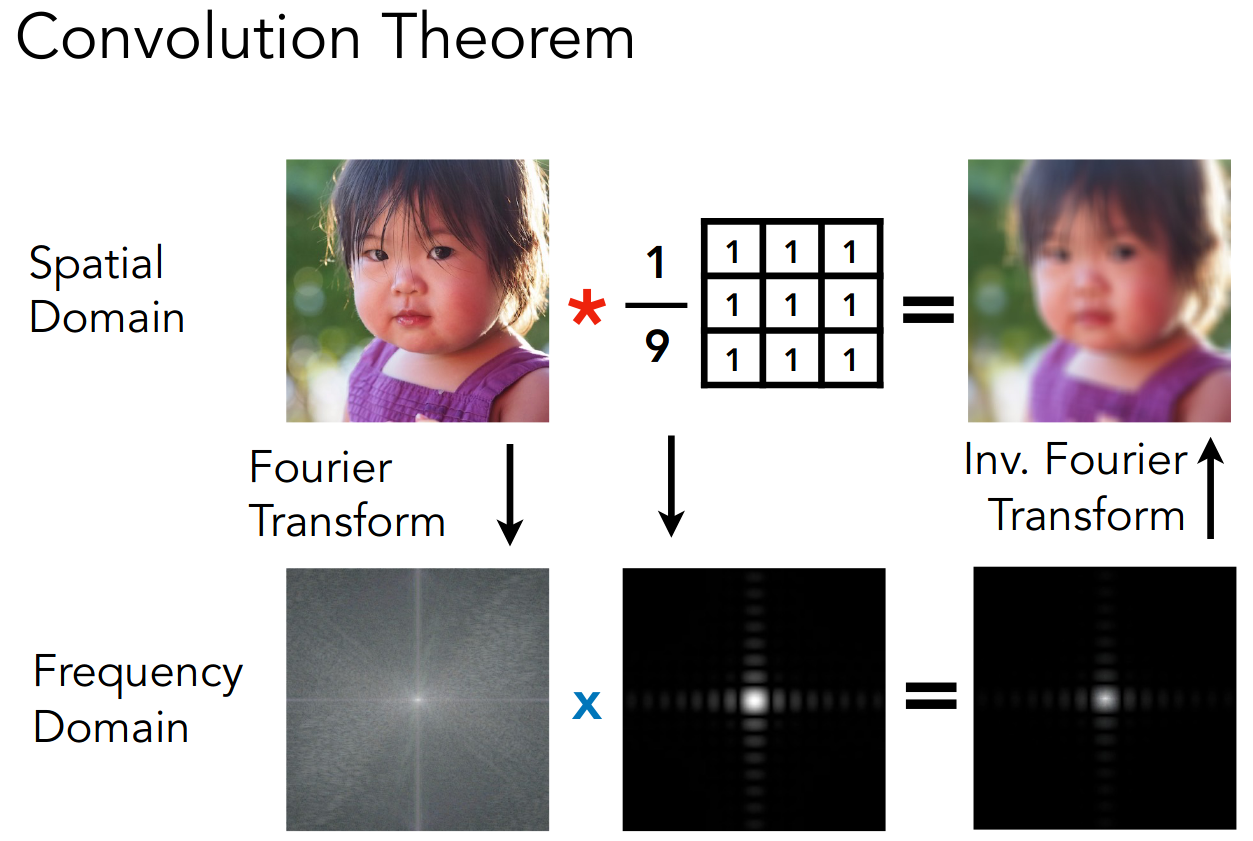
a4bbab3541f749abb38a97d278541a77.png

Antialiasing in practice

以此为基础，有如下解决 Aliasing Artifacts 的方案

011bd47316bd478a945df01bd5289d92.png

其他技术

着色（光照与基本着色模型）

Z-buffering

光栅化最后的内容

主要解决 visibility / occlusion 的问题

思想如下

算法伪代码如下

for (each triangle T)
  for (each sample (x,y,z) in T)
    if (z < zbuffer[x,y])        // closest sample so far
      framebuffer[x,y] = rgb;    // update color
      zbuffer[x,y] = z;          // update depth
    else
      ;                          // do nothing, this sample is occluded

两个注意点

一个简单的例子

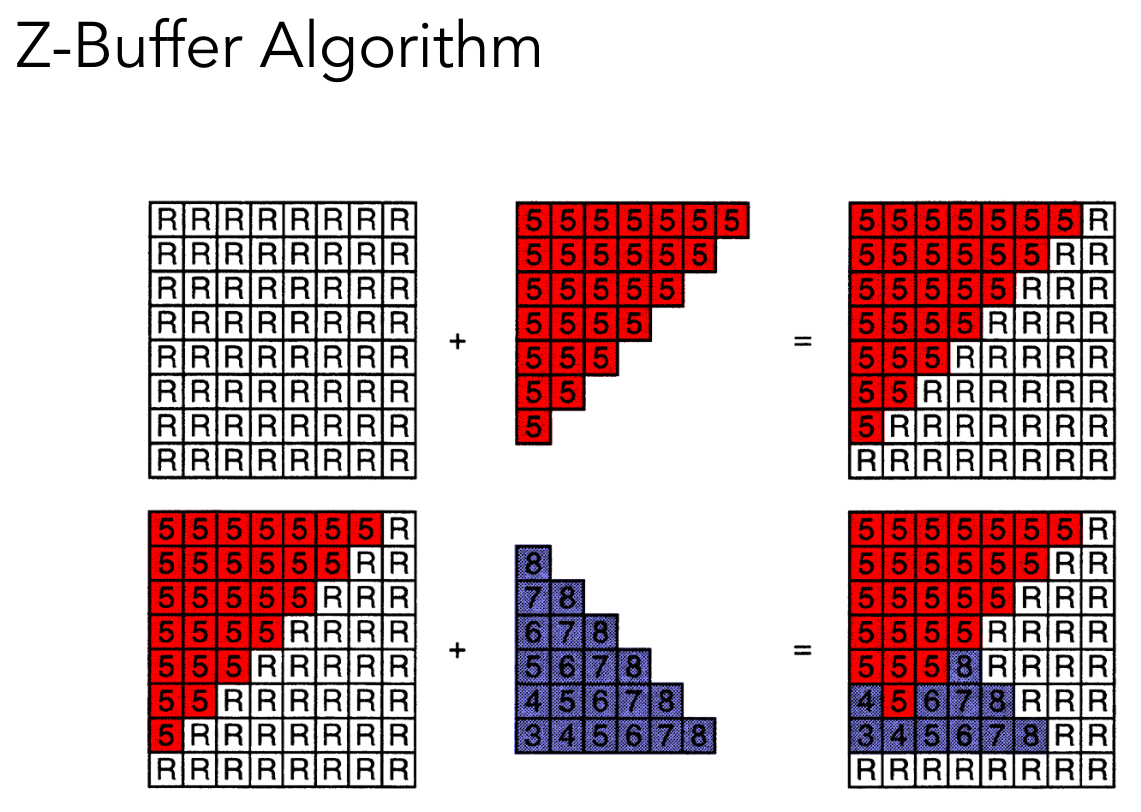
57e5504559134dea87ec2179f11737b4.png

若每个三角形占据常数个像素，算法复杂度与三角形个数成线性关系

Shading

我们给着色一个定义

The darkening or coloring of an illustration or diagram with parallel lines or a block of color.

The process of applying a material to an object.

下面考虑一个简单的着色模型

Blinn-Phong Reflectance Model

e56aa3da51ed4e92a09ed8204aafbe46.png

从上到下依次为

需要给着色点进行形式化描述

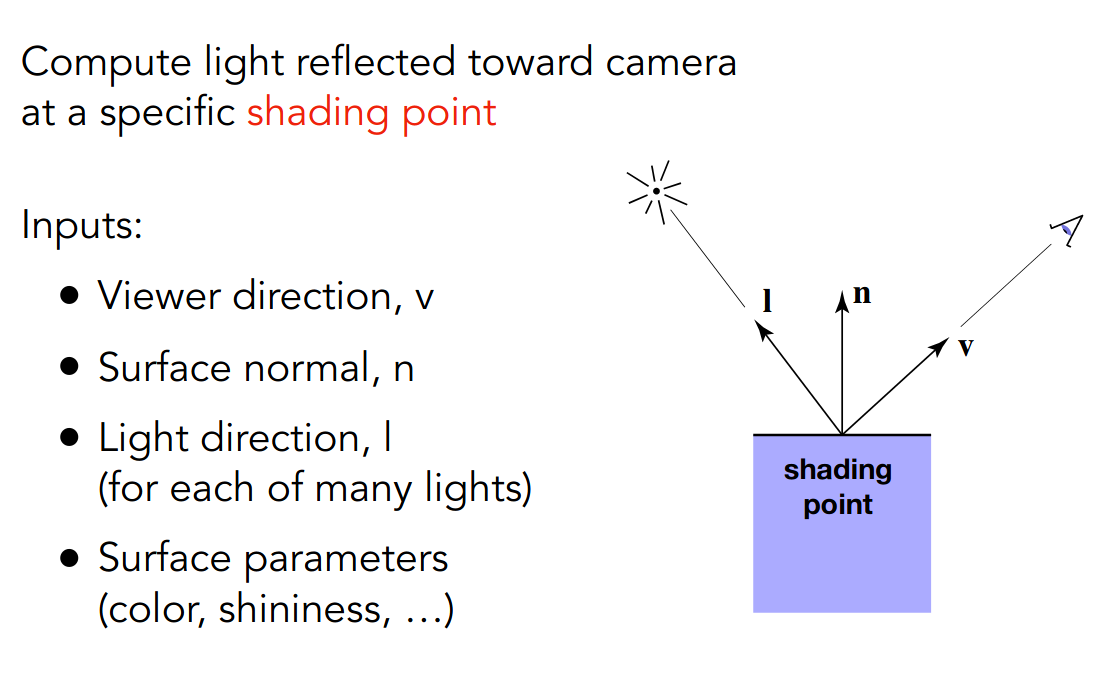
ca0ece306c09400dab7f696ab0664ea9.png

也就是考虑观察方向，光线方向和表面的法向

均为单位向量

需要注意着色具有局部性（近似为平面才有法向），因而不会因为光线的遮挡而产生阴影

shading ≠ shadow

下面给出漫反射的一个近似公式

1735a417b78a46d1ac48d8e9c81d1669.png

注意里面的 I 为光能，r 代表光源和着色点的距离

通过球壳表面光能固定推导出平方反比的关系

而 k 是材质与漫反射相关的系数

注意对于漫反射而言，无论观察方向，着色都是一致的

PA2

color

三角形一

三角形二

run

可以这样指定参数

./build/Rasterizer pa2.png
mv pa2.png ~/Desktop/virtual-machine-repository/post/games101.assets/

note

// Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle &t) {
  auto v = t.toVector4();


  // TODO : Find out the bounding box of current triangle.
  // iterate through the pixel and find if the current pixel is inside the
  // triangle
  int xmin = std::floor(std::min(t.v[0].x(), std::min(t.v[1].x(), t.v[2].x())));
  int xmax = std::ceil(std::max(t.v[0].x(), std::max(t.v[1].x(), t.v[2].x())));
  int ymin = std::floor(std::min(t.v[0].y(), std::min(t.v[1].y(), t.v[2].y())));
  int ymax = std::ceil(std::max(t.v[0].y(), std::max(t.v[1].y(), t.v[2].y())));


  for (int i = xmin; i <= xmax; ++i) {
    for (int j = ymin; j <= ymax; ++j) {
      float x = i + 0.5;
      float y = j + 0.5;


      if (insideTriangle(x, y, t.v)) {
        // If so, use the following code to get the interpolated z value.
        auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
        float w_reciprocal =
            1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
        float z_interpolated = alpha * v[0].z() / v[0].w() +
                               beta * v[1].z() / v[1].w() +
                               gamma * v[2].z() / v[2].w();
        z_interpolated *= w_reciprocal;


        // TODO : set the current pixel (use the set_pixel function) to the
        // color of
        // the triangle (use getColor function) if it should be painted.
        if (-z_interpolated < depth_buf[get_index(i, j)]) {
          depth_buf[get_index(i, j)] = -z_interpolated;
          frame_buf[get_index(i, j)] = t.getColor();
        }
      }
    }
  }
}

先创建 bounding box

然后遍历每个像素，注意像素中心的屏幕空间坐标需要加上 0.5

使用 insideTriangle 判断是否在三角形内部

static bool insideTriangle(float x, float y, const Vector3f *_v) {
  // TODO : Implement this function to check if the point (x, y) is inside the
  // triangle represented by _v[0], _v[1], _v[2]
  Eigen::Vector3f ab(_v[0].x() - _v[1].x(), _v[0].y() - _v[1].y(), _v[0].z() - _v[1].z());
  Eigen::Vector3f bc(_v[1].x() - _v[2].x(), _v[1].y() - _v[2].y(), _v[1].z() - _v[2].z());
  Eigen::Vector3f ca(_v[2].x() - _v[0].x(), _v[2].y() - _v[0].y(), _v[2].z() - _v[0].z());


  Eigen::Vector3f au(_v[0].x() - x, _v[0].y() - y, _v[0].z() - 0);
  Eigen::Vector3f bu(_v[1].x() - x, _v[1].y() - y, _v[1].z() - 0);
  Eigen::Vector3f cu(_v[2].x() - x, _v[2].y() - y, _v[2].z() - 0);


  auto res1 = ab.cross(au).z();
  auto res2 = bc.cross(bu).z();
  auto res3 = ca.cross(cu).z();


  return (res1 > 0 && res2 > 0 && res3 > 0) ||
         (res1 < 0 && res2 < 0 && res3 < 0);
}

这里将参数改成了 float

使用三维向量进行外积，z 分量为 0

最后只要看外积出的向量的 z 分量即可

(a1,a2,a3)×(b1,b2,b3)=(a2b3−a3b2,a3b1−a1b3,a1b2−a2b1)(a_1,a_2,a_3) \times (b_1,b_2,b_3)=(a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1)

然后计算出插值深度值，并与深度缓冲区中的相应值进行比较

这里奇怪的是需要对插值深度值取负，否则深度关系就反了

感觉哪里实现错了

最后更新 depth_buf 和 frame_buf 即可

使用 get_index 函数将二维坐标转换为一维坐标

后来发现是透视投影矩阵有点问题

由于传入 get_projection_matrix 函数的 zNear 和 zFar 是正数

所以实际上要将透视投影矩阵的 n 和 f 取负

M=[n0000n0000n+f−nf0010]M = \begin{bmatrix} n & 0 & 0 & 0 \newline 0 & n & 0 & 0 \newline 0 & 0 & n + f & -nf \newline 0 & 0 & 1 & 0 \end{bmatrix}

简单的做法就是这样

M=[n0000n0000n+f−nf00−10]M = \begin{bmatrix} n & 0 & 0 & 0 \newline 0 & n & 0 & 0 \newline 0 & 0 & n + f & -nf \newline 0 & 0 & -1 & 0 \end{bmatrix}

这样的话就不需要对插值深度值取负了

pic

修正透视投影矩阵后

大小有点怪怪的

f54978d6c14b47fe8b2655f8f44efb8d.png

antialiasing

框架不变，只是在填充 frame_buf 时取平均

        if (z_interpolated < depth_buf[get_index(i, j)]) {
          depth_buf[get_index(i, j)] = z_interpolated;
          int sum{};
          sum += static_cast<int>(insideTriangle(x - 0.25, y - 0.25, t.v));
          sum += static_cast<int>(insideTriangle(x - 0.25, y + 0.25, t.v));
          sum += static_cast<int>(insideTriangle(x + 0.25, y - 0.25, t.v));
          sum += static_cast<int>(insideTriangle(x + 0.25, y + 0.25, t.v));
          frame_buf[get_index(i, j)] = t.getColor() * (sum / 4.0);
        }

确实优化了一丢丢

d035fa09544f4d289c89a59d24f692f3.png

着色（着色频率、图形管线、纹理映射）

Blinn-Phong reflectance model

接着上节课的内容

下面给出高光的一个近似公式

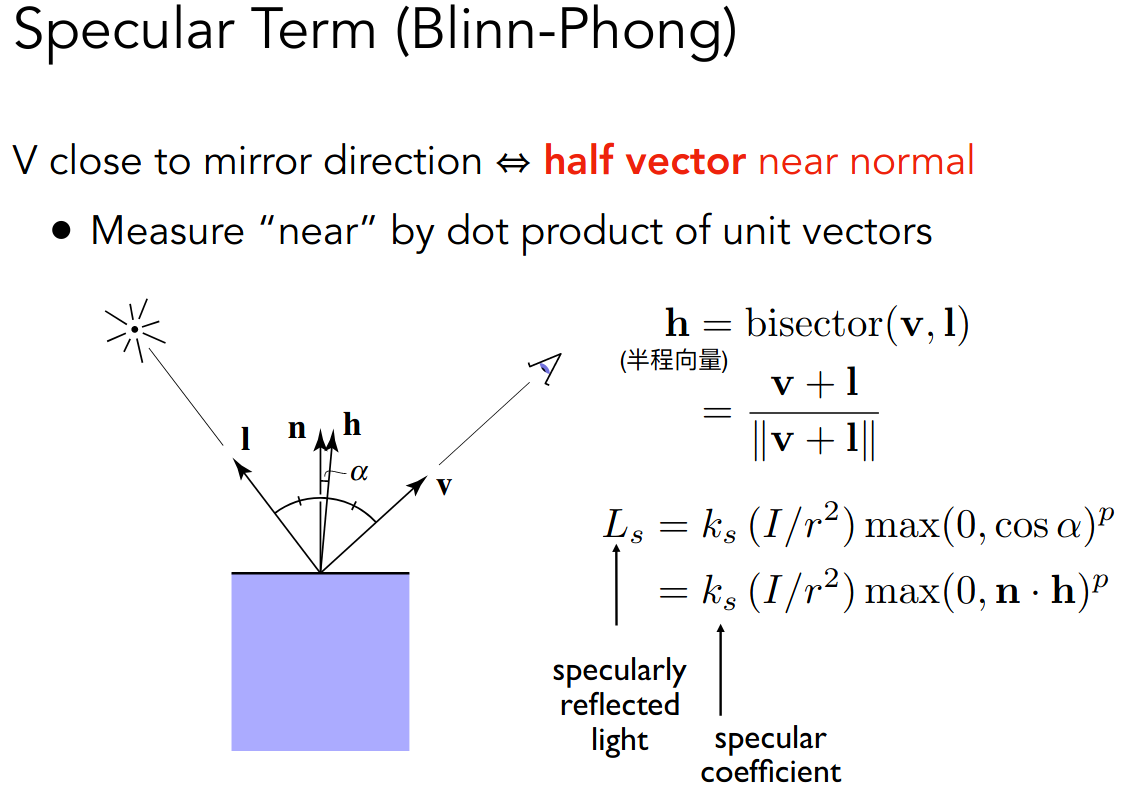
d5d270696119431c9c8d03224f84a5c2.png

这里进行了一次转化，对于高光而言，可以近似认为是镜面反射，设反射光为 I’

那么有角度关系

α=arccos⁡(n⃗,h⃗)=12arccos⁡(I′⃗,v⃗)\alpha = \arccos(\vec{n},\vec{h}) = \frac{1}{2} \arccos(\vec{I'},\vec{v})

也就是转化为半程向量和法向量之间的夹角

而常数 p 可以用来控制 reflection lobe

对于环境光而言，在固定光能和系数的情形下，可以认为是常数

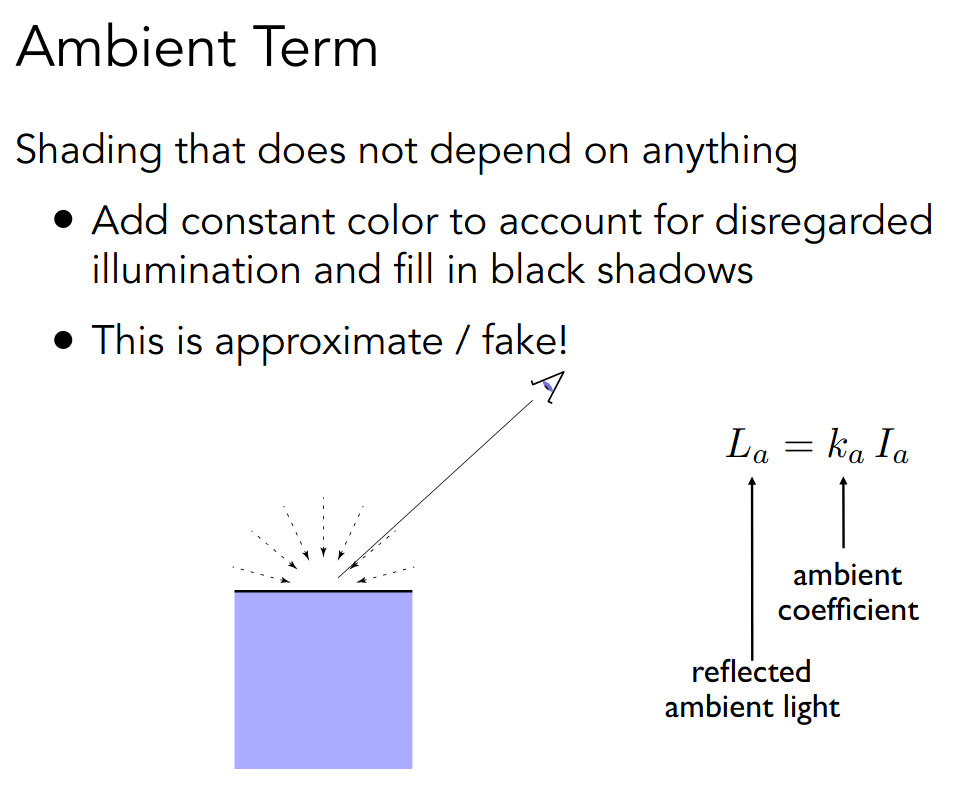
d8bfceebe681443ca022575380497639.png

于是 Blinn-Phong Reflectance Model 总结如下

9d56f71bf11343ac9ab5e8563d8364f9.png

Shading Frequencies

一图胜千言

ce58334484e84905ba0407525aecfccd.png

Flat 是每个三角形视为一个着色点

Gouraud 是每个三角形的顶点视为一个着色点，顶点的法向量通过对周围三角形的法向量取均值得到

Phong 是每个像素视为一个着色点，像素的法向量通过插值得到

Graphics (Real-time Rendering) Pipeline

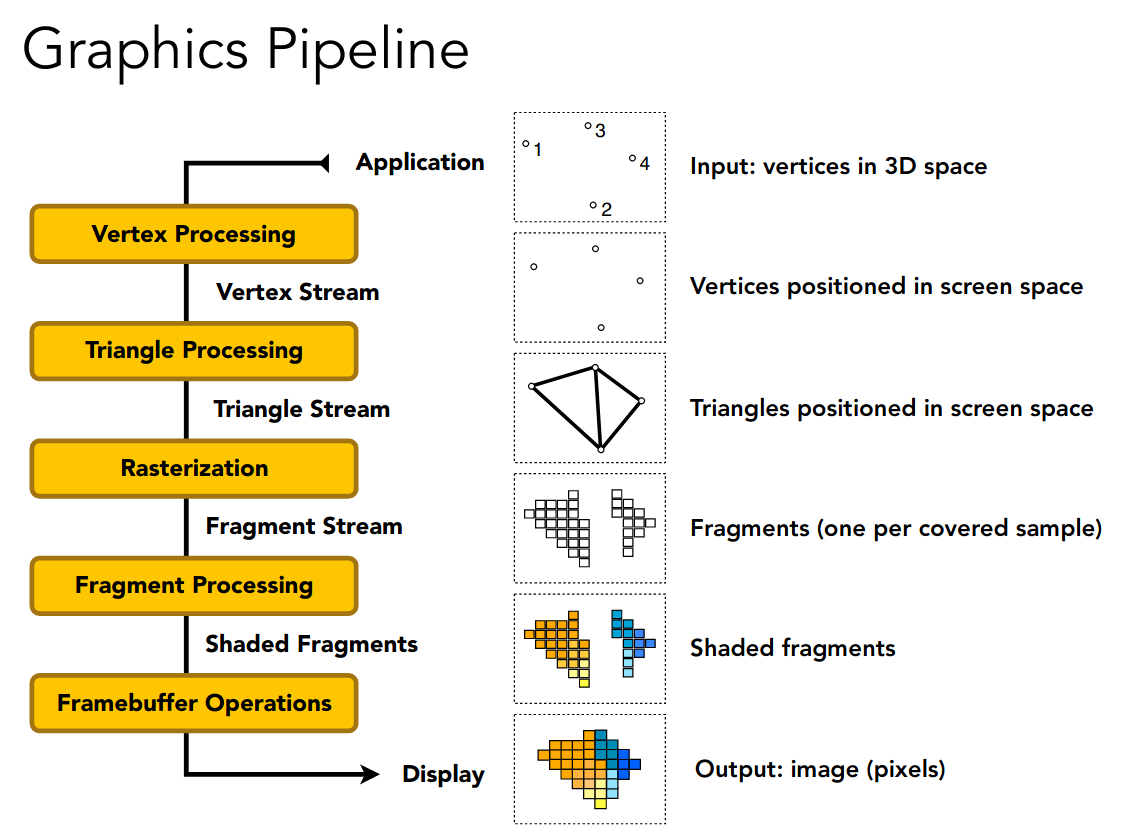
b255149a4204494c9fcb1d5b7e92f2a5.png

这里相当于总结了目前所学的内容

引入了顶点处理的步骤

从而着色可以选择在 Vertex Processing 中进行，着色频率为 Gouraud

也可以选择在 Fragment Processing 中进行，着色频率为 Phong 或 Flat

Shader Programs

着色器就是在某些阶段处理着色的程序

Example GLSL fragment shader program

uniform sampler2D myTexture; // program parameter
uniform vec3 lightDir;   // program parameter
varying vec2 uv;    // per fragment value (interp. by rasterizer)
varying vec3 norm;   // per fragment value (interp. by rasterizer)
void diffuseShader()
{
  vec3 kd;
  kd = texture2d(myTexture, uv);    // material color from texture
  kd *= clamp(dot(–lightDir, norm), 0.0, 1.0);  // Lambertian shading model
  gl_FragColor = vec4(kd, 1.0);    // output fragment color
}

描述了对单个顶点或像素进行的操作

另外推荐一个网站 https://www.shadertoy.com/

GPU

实现图形管线的硬件便是 GPU

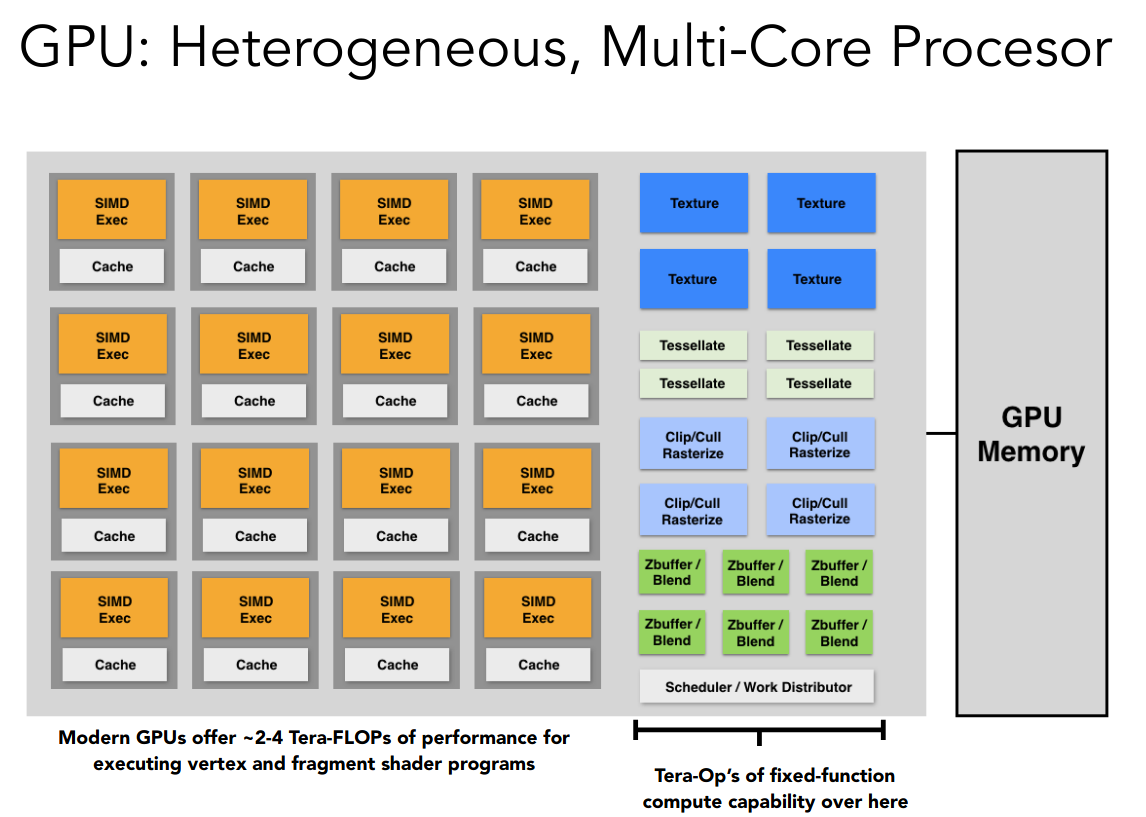
1bd43bc29c4c409fb7f3a3d1bc4c4ad4.png

多核心，高度并行

Texture Mapping

独眼巨人警告

相当于从屏幕空间到纹理空间的映射

定义了 Blinn-Phong reflectance model 公式的中的 k 值

我们以漫反射的 k 值为例

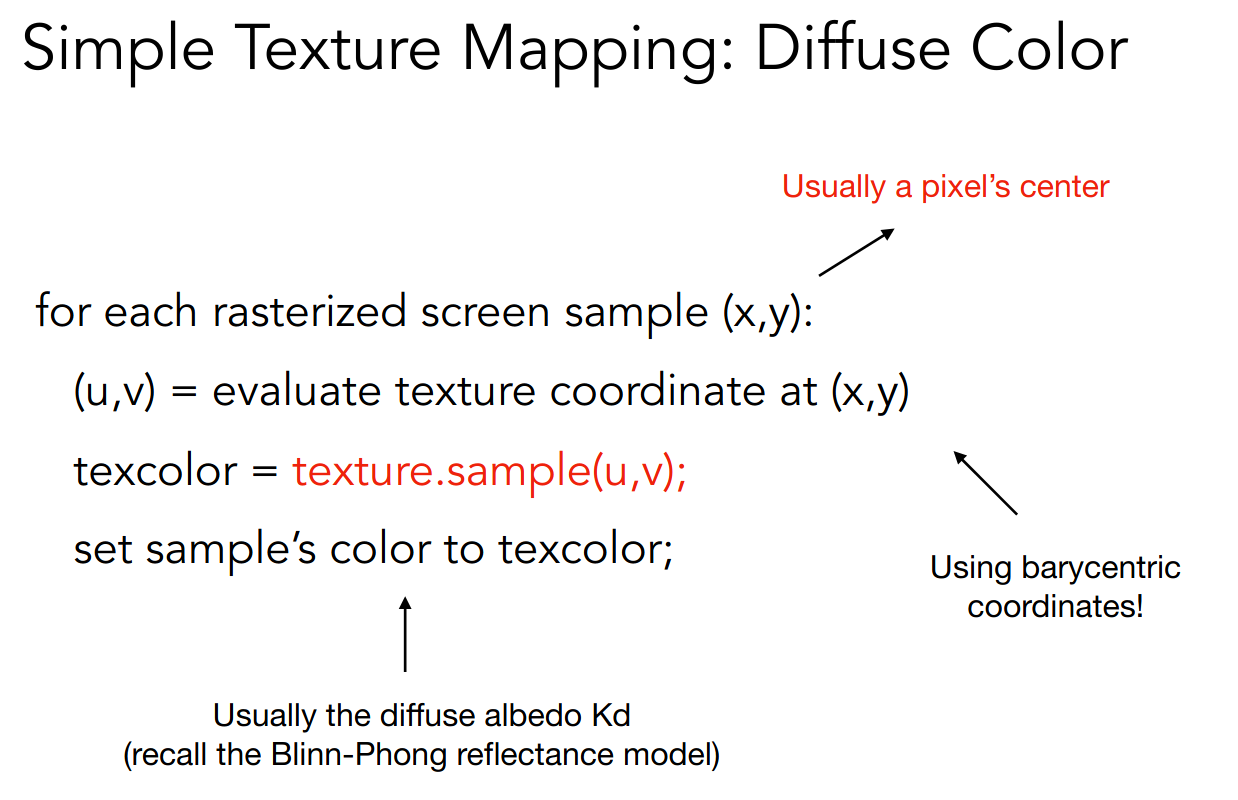
9b1d21c620e2422989c7daeee35421ed.png

得到纹理空间的坐标后，还可能需要插值处理

感觉图中箭头指向的位置不太对

着色（插值、高级纹理映射）

Barycentric Coordinates

之前在许多地方都遇到了插值

通过三角形的重心坐标实现插值，公式如下

dd0ebc1f72514178b05b4f91a5a81f11.png

面积关系可以直观的理解

△ABP:△BCP:△CAP=γ:α:β\triangle_{ABP} : \triangle_{BCP} : \triangle_{CAP} = \gamma : \alpha : \beta

我们以插值颜色为例

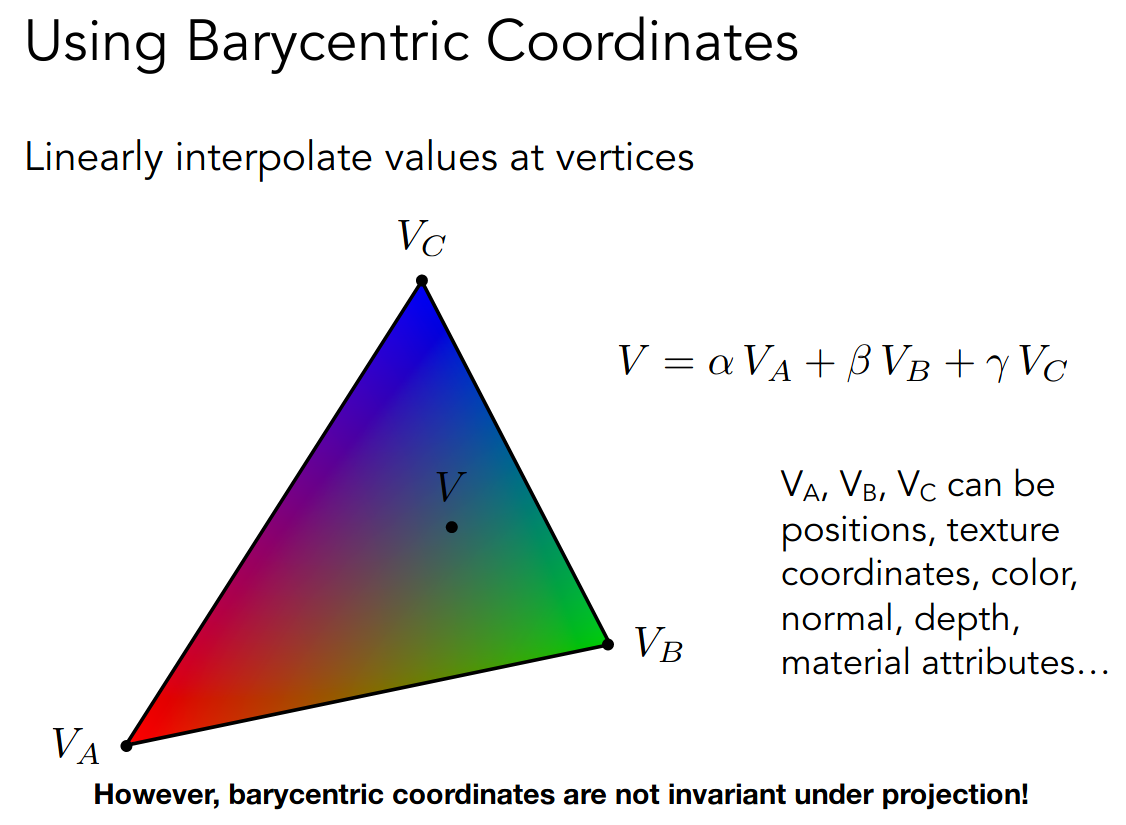
0145ff092c2947fda521c71da812a43c.png

需要注意在投影变换下插值坐标可能发生变化

所以三维的属性在投影之前就应该进行插值

Texture antialiasing

What if the texture is too small?

纹理的分辨率太低

我们定义 pixel on a texture 为 texel

下面介绍双线性插值

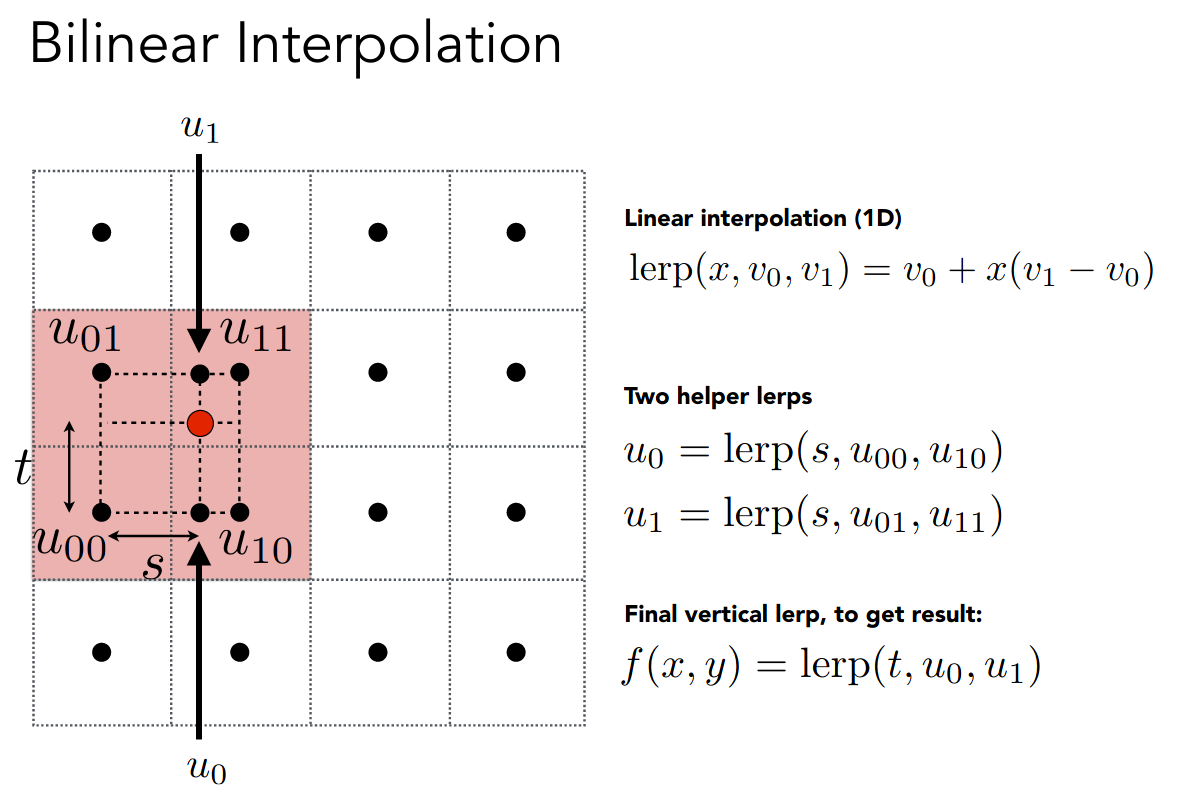
0bb584a27b594c2192123f380108ac3c.png

红色点是映射之后的坐标，而黑色点则是 texel

找最近的四个点，在两个方向线性插值即可

可以认为是正方形的重心坐标

当然还有效果更好的插值方法，如双三次插值 Bicubic Interpolation

What if the texture is too large?

通常是映射后所占据的纹理空间过大

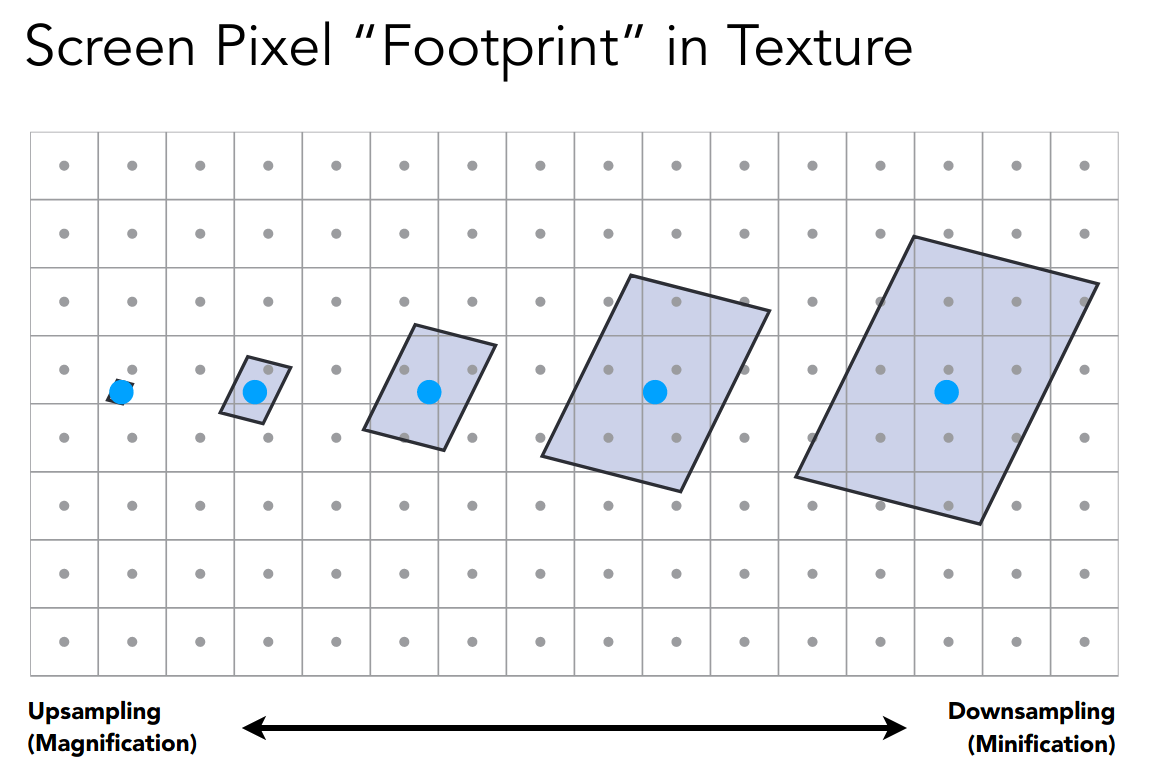
2130b6eaafe5438e98e83fc3414f0a2b.png

当然超采样是一种解决方案

我们考虑换一个思路，之前都是试图求纹理空间某个点对应的值

现在我们尝试求纹理空间某个范围对内应的统计量，如平均值或极值

这实际上就是二维的 range queries

有一个近似的解决方案为 Mipmap

Allowing (fast, approx., square) range queries

c32e01e0b8ee47ff82c8559644ad19eb.png

先对纹理空间进行预处理，所占用的额外空间不超过原占用空间的三分之一

然后通过某种方式得到查询范围的边长 L，并计算层级 D

D=log⁡2(L)D = \log_2(L)

接着在层级中进行双线性插值

最后在层级间进行线性插值，因为 D 可能不是整数

示意图如下，这也被称为三线性插值

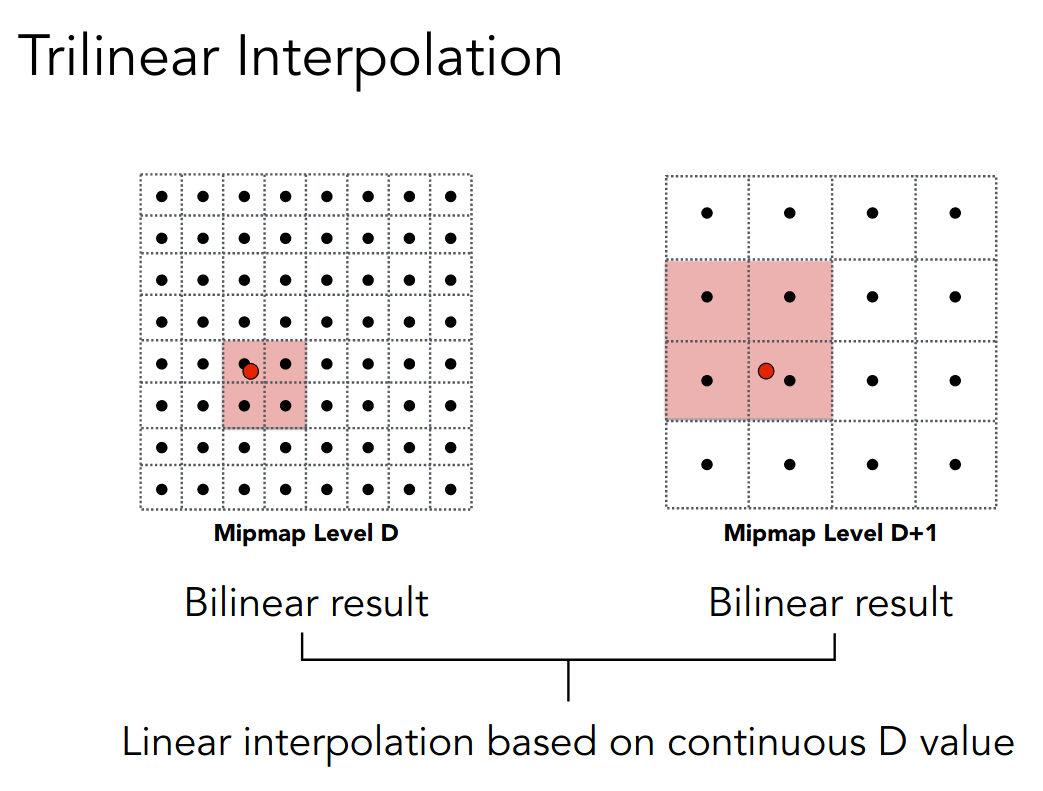
63ab94265ef74c94a471f0b73b9d11c0.png

然而 Mipmap 对非正方形的处理误差会较大

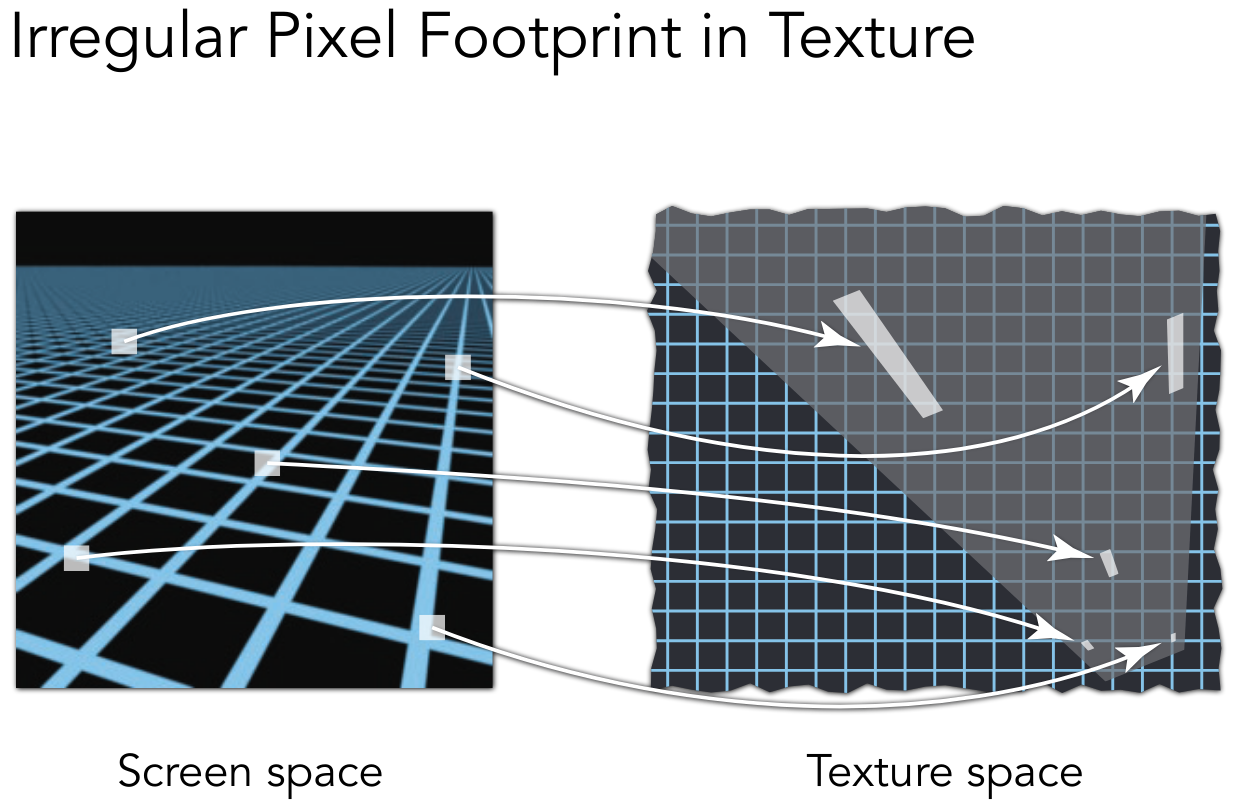
6c88da4a5a1e4504b11ce9ef0e95c978.png

于是便有了各向异性过滤 Anisotropic Filtering，来处理矩阵的情形

72affc46ef3842138432931ac453261b.png

所占用的额外空间不超过原占用空间的三倍

然而各向异性过滤对于不规则的空间仍不易处理，可以参考 EWA filtering

PA3

run

./build/Rasterizer pa3-normal.png normal
mv pa3-normal.png ~/Desktop/virtual-machine-repository/post/games101.assets/

似乎不支持实时旋转

interface

需要使用的 eigen 方法

note

首先需要修改一下 models 的路径

修改函数 rasterize_triangle

依次实现颜色、法向量、纹理颜色、纹理坐标的插值

        if (z_interpolated < depth_buf[get_index(i, j)]) {
          depth_buf[get_index(i, j)] = z_interpolated;


          // TODO: Interpolate the attributes:
          // auto interpolated_color
          // auto interpolated_normal
          // auto interpolated_texcoords
          // auto interpolated_shadingcoords
          auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0],
                                                t.color[1], t.color[2], 1);
          auto interpolated_normal = interpolate(
              alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1);
          auto interpolated_texcoords =
              interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1],
                          t.tex_coords[2], 1);
          auto interpolated_shadingcoords =
              interpolate(alpha, beta, gamma, view_pos[0], view_pos[1],
                          view_pos[2], 1);


          fragment_shader_payload payload(
              interpolated_color, interpolated_normal.normalized(),
              interpolated_texcoords, texture ? &*texture : nullptr);
          payload.view_pos = interpolated_shadingcoords;


          // Instead of passing the triangle's color directly to the frame
          // buffer, pass the color to the shaders first to get the final color.
          auto pixel_color = fragment_shader(payload);
          frame_buf[get_index(i, j)] = pixel_color;
        }

最终的颜色通过调用着色器函数 fragment_shader 得到

另外 insideTriangle 的参数类型有细微变化，Vector3f -> Vector4f

使用框架代码，将整型改为浮点型

修改函数 get_projection_matrix

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar) {
  // TODO: Use the same projection matrix from the previous assignments
  Eigen::Matrix4f projection;


  float yTop = zNear * std::tan(eye_fov / 360 * MY_PI);
  float xRight = yTop * aspect_ratio;


  // clang-format off
  Eigen::Matrix4f ortho_scale;
  ortho_scale << 1 / xRight, 0, 0, 0,
                 0, 1 / yTop, 0, 0,
                 0, 0, 2 / (zFar - zNear), 0,
                 0, 0, 0, 1;


  Eigen::Matrix4f ortho_trans;
  ortho_trans << 1, 0, 0, 0,
                 0, 1, 0, 0,
                 0, 0, 1, (zNear + zFar) / 2,
                 0, 0, 0, 1;


  Eigen::Matrix4f persp;
  persp << zNear, 0, 0, 0,
           0, zNear, 0, 0,
           0, 0, zNear + zFar, -zNear * zFar,
           0, 0, -1, 0; // attention -1


  projection = ortho_scale
               * ortho_trans
               * persp
               * projection;
  // clang-format on


  std::cout << projection << std::endl;


  return projection;
}

之前的实现没有考虑到 ortho_trans

可以通过注释 clang-format 调整自动格式化的范围

修改函数 phong_fragment_shader，通过 Blinn-Phong reflectance model 计算 Fragment Color

Eigen::Vector3f
texture_fragment_shader(const fragment_shader_payload &payload) {
  Eigen::Vector3f return_color = {0, 0, 0};
  if (payload.texture) {
    // TODO: Get the texture value at the texture coordinates of the current
    // fragment
    return_color = payload.texture->getColor(payload.tex_coords.x(),
                                             payload.tex_coords.y());
  }
  Eigen::Vector3f texture_color;
  texture_color << return_color.x(), return_color.y(), return_color.z();


  Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
  Eigen::Vector3f kd = texture_color / 255.f;
  Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);


  auto l1 = light{{20, 20, 20}, {500, 500, 500}};
  auto l2 = light{{-20, 20, 0}, {500, 500, 500}};


  std::vector<light> lights = {l1, l2};
  Eigen::Vector3f amb_light_intensity{10, 10, 10};
  Eigen::Vector3f eye_pos{0, 0, 10};


  float p = 150;


  Eigen::Vector3f color = texture_color;
  Eigen::Vector3f point = payload.view_pos;
  Eigen::Vector3f normal = payload.normal;
  Eigen::Vector3f view_vec = eye_pos - point;
  Eigen::Vector3f result_color = {0, 0, 0};


  for (auto &light : lights) {
    // TODO: For each light source in the code, calculate what the *ambient*,
    // *diffuse*, and *specular* components are. Then, accumulate that result on
    // the *result_color* object.
    Eigen::Vector3f light_vec = light.position - point;
    Eigen::Vector3f half_vec = view_vec + light_vec;
    float n_dot_l = normal.dot(light_vec.normalized());
    float n_dot_h = normal.dot(half_vec.normalized());
    float r_square = light_vec.dot(light_vec);
    result_color += ka.cwiseProduct(amb_light_intensity);
    result_color +=
        kd.cwiseProduct(light.intensity) / r_square * std::max(0.f, n_dot_l);
    result_color += ks.cwiseProduct(light.intensity) / r_square *
                    std::pow(std::max(0.f, n_dot_h), p);
  }


  return result_color * 255.f;
}

直接看有纹理的版本

修改函数 bump_fragment_shader，实现 Bump mapping

Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload &payload) {
  assert(payload.texture);


  Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
  Eigen::Vector3f kd = payload.color;
  Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);


  auto l1 = light{{20, 20, 20}, {500, 500, 500}};
  auto l2 = light{{-20, 20, 0}, {500, 500, 500}};


  std::vector<light> lights = {l1, l2};
  Eigen::Vector3f amb_light_intensity{10, 10, 10};
  Eigen::Vector3f eye_pos{0, 0, 10};


  float p = 150;


  Eigen::Vector3f color = payload.color;
  Eigen::Vector3f point = payload.view_pos;
  Eigen::Vector3f normal = payload.normal;


  float kh = 0.2, kn = 0.1;


  // TODO: Implement bump mapping here
  // Let n = normal = (x, y, z)
  // Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
  // Vector b = n cross product t
  // Matrix TBN = [t b n]
  // dU = kh * kn * (h(u+1/w,v)-h(u,v))
  // dV = kh * kn * (h(u,v+1/h)-h(u,v))
  // Vector ln = (-dU, -dV, 1)
  // Normal n = normalize(TBN * ln)
  Eigen::Vector3f t{
      normal.x() * normal.y() /
          std::sqrt(normal.x() * normal.x() + normal.z() * normal.z()),
      std::sqrt(normal.x() * normal.x() + normal.z() * normal.z()),
      normal.z() * normal.y() /
          std::sqrt(normal.x() * normal.x() + normal.z() * normal.z())};
  Eigen::Vector3f b{normal.cross(t)};
  Eigen::Matrix3f TBN;
  // clang-format off
  TBN << t.x(), b.x(), normal.x(),
         t.y(), b.y(), normal.y(),
         t.z(), b.z(), normal.z();
  // clang-format on
  float u = payload.tex_coords.x();
  float v = payload.tex_coords.y();
  int w = payload.texture->width;
  int h = payload.texture->height;
  float dU = kh * kn *
             (payload.texture->getColor(u + 1.f / w, v).norm() -
              payload.texture->getColor(u, v).norm());
  float dV = kh * kn *
             (payload.texture->getColor(u, v + 1.f / h).norm() -
              payload.texture->getColor(u, v).norm());
  Eigen::Vector3f ln{-dU, -dV, 1.f};
  normal = (TBN * ln).normalized();


  Eigen::Vector3f result_color = {0, 0, 0};
  result_color = normal;


  return result_color * 255.f;
}

这是后面的内容，属实有点超纲

注意 h(u,v) = texture_color(u,v).norm

其中 u,v 是 tex_coords

w,h 是 texture 的宽度与高度

displacement_fragment_shader 相当于多了 Blinn-Phong reflectance model 的部分

pic

感觉视角和 Bump mapping 实现的有点问题

pa3-normal

ecd8c03ddc134fd49a4f33a80cb1806f.png

pa3-phong

3bb299946e744713a44288ec77013441.png

pa3-texture

ea416ea0469b42e883406c47cf1aa659.png

pa3-bump

de2adfbfd7d147079f965283e1b99302.png

pa3-displacement

897ac7ef2a894edc878eed1aa4fed9fe.png

todo

几何（基本表示方法）

Applications of textures

着色最后的内容

一些纹理的应用

In modern GPUs, texture = memory + range query (filtering)

General method to bring data to fragment calculations

Environment Map

环境光贴图可以让模型反射出周围环境的样子

ad224d6321914ae6b447da6e13da0a86.png

Bump Mapping / Normal mapping

使用纹理空间表示 height 或 normal

以二维的 Bump Mapping 为例，扰动法线

e569581a29b943bcaa9c847253989f9a.png

Displacement mapping

已经不太懂了

https://zhuanlan.zhihu.com/p/340786255

Ambient occlusion texture map

预先计算环境光遮蔽，并反映在纹理上

shadow

3D Textures

Introduction to geometry

Implicit Representations

Inside/Outside Tests Easy

解析式

f(x,y,z)=x2+y2+z2−1f(x,y,z)=x^2+y^2+z^2-1

使用布尔运算组合

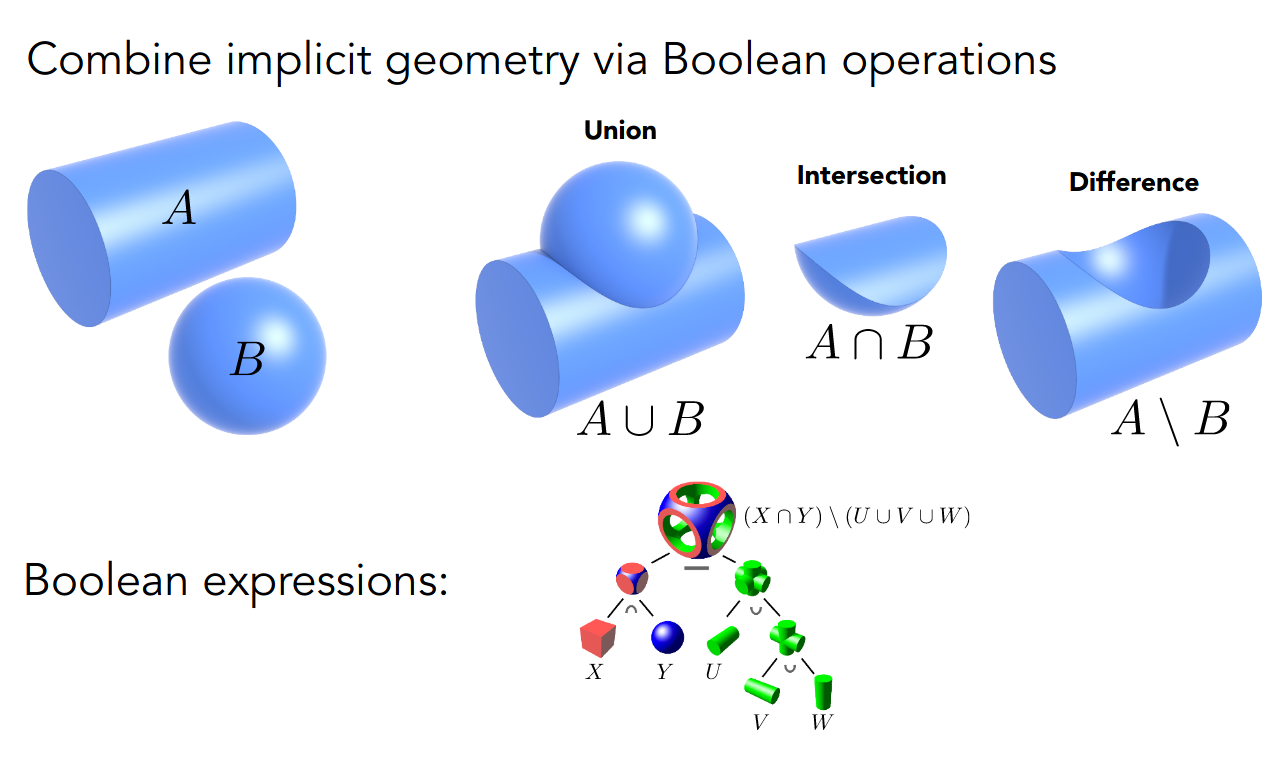
6e4a93a30c1a4d658a5c9fa2610e58d0.png

记录到物体的最短距离

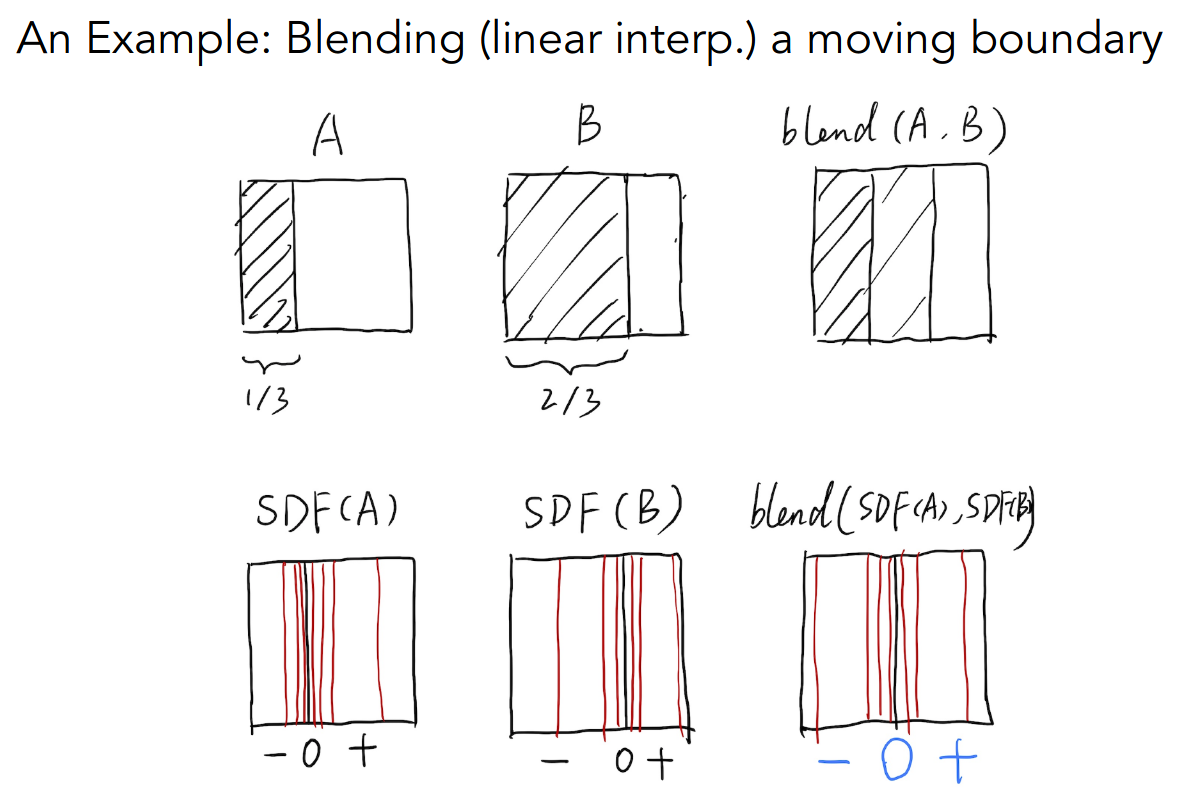
c076edc77f274a82a1fffbd43ac74634.png

例如直接线性插值，中间部分就是灰色

使用有向距离函数变换后再 blend

中间部分的距离就是零，变换回来正好左边黑右边白

类似等高线

分形结构

Explicit Representations

Sampling Is Easy

参数方程

f:R2→R3;(u,v)→(x,y,z)f:\R^2 \to \R^3;(u,v) \to (x,y,z)

如

f(u,v)=(cosu⋅sinv,sinu⋅sinv,cosv)f(u,v)=(cosu \cdot sinv,sinu \cdot sinv,cosv)

几何（曲线与曲面）

Explicit Representations

顾名思义，一堆密集的点形成几何图形

存储顶点和多边形

PA3 的 models 文件夹里有这种类型的文件

https://en.wikipedia.org/wiki/Wavefront_.obj_file

Curves

主要讲贝塞尔曲线 Bézier Curves

de Casteljau Algorithm

直接从代数的角度计算

以三次贝塞尔曲线为例，有四个控制点，一个参数

所以贝塞尔曲线是 Explicit Representations

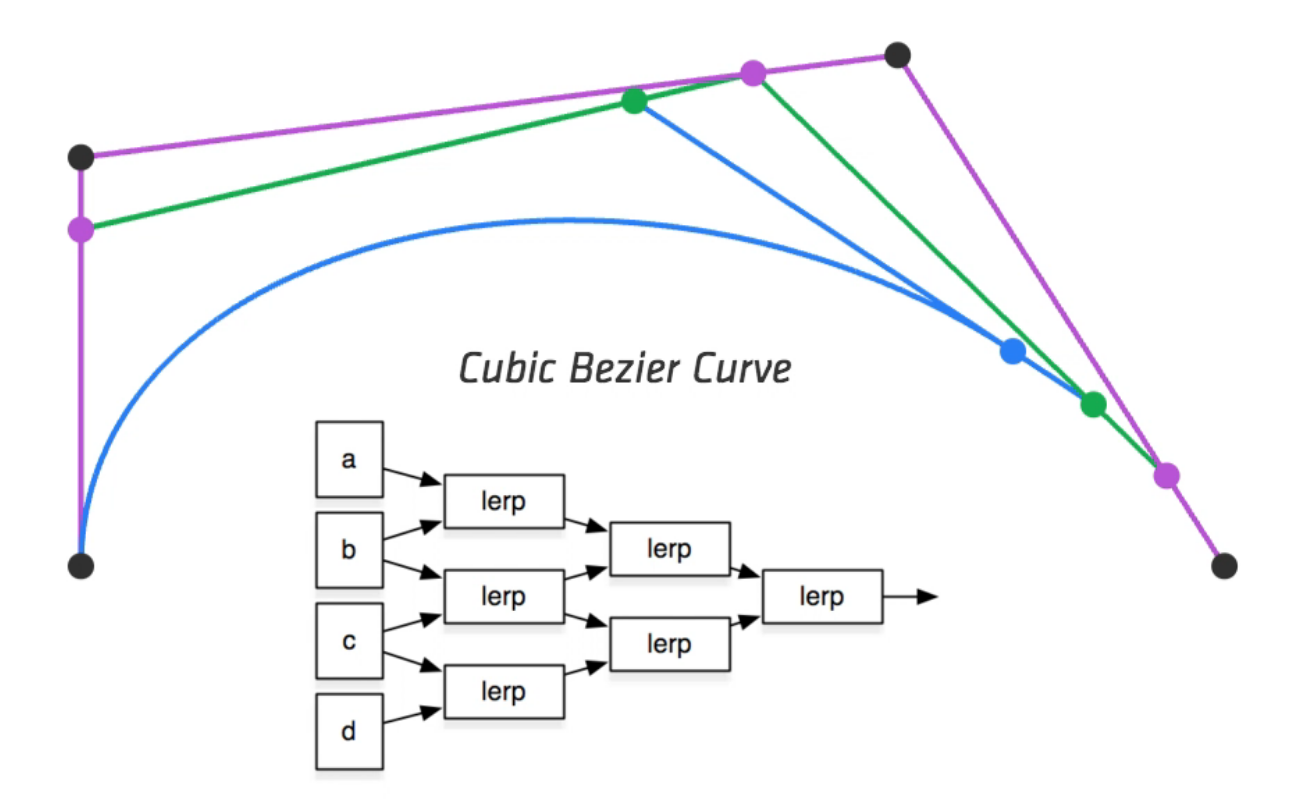
66927a12c20d4b40b2bcde4a3d480f80.png

控制点之间做线性插值，得到新的控制点

然后递归进行，最终得到对应参数的点

Algebraic Formula

以二次贝塞尔曲线为例

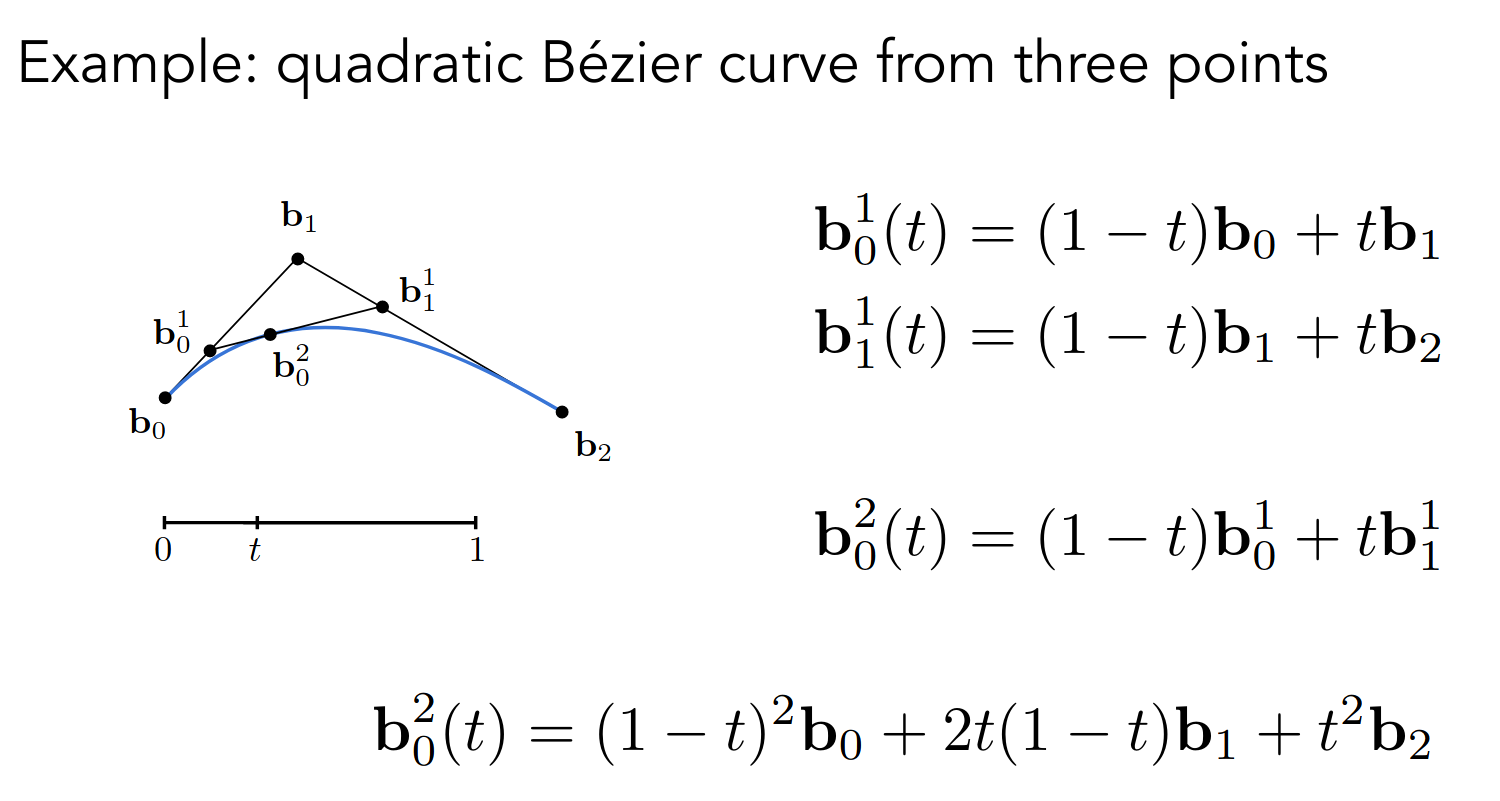
7bbb4bfa3f244cc3943321891b53ca11.png

观察形式类似于二项展开

不难推出，对于 nn 次贝塞尔曲线，有

9e06a0743e634ca788faa5192e31d694.png

Properties of Bézier Curves

以三次贝塞尔曲线为例

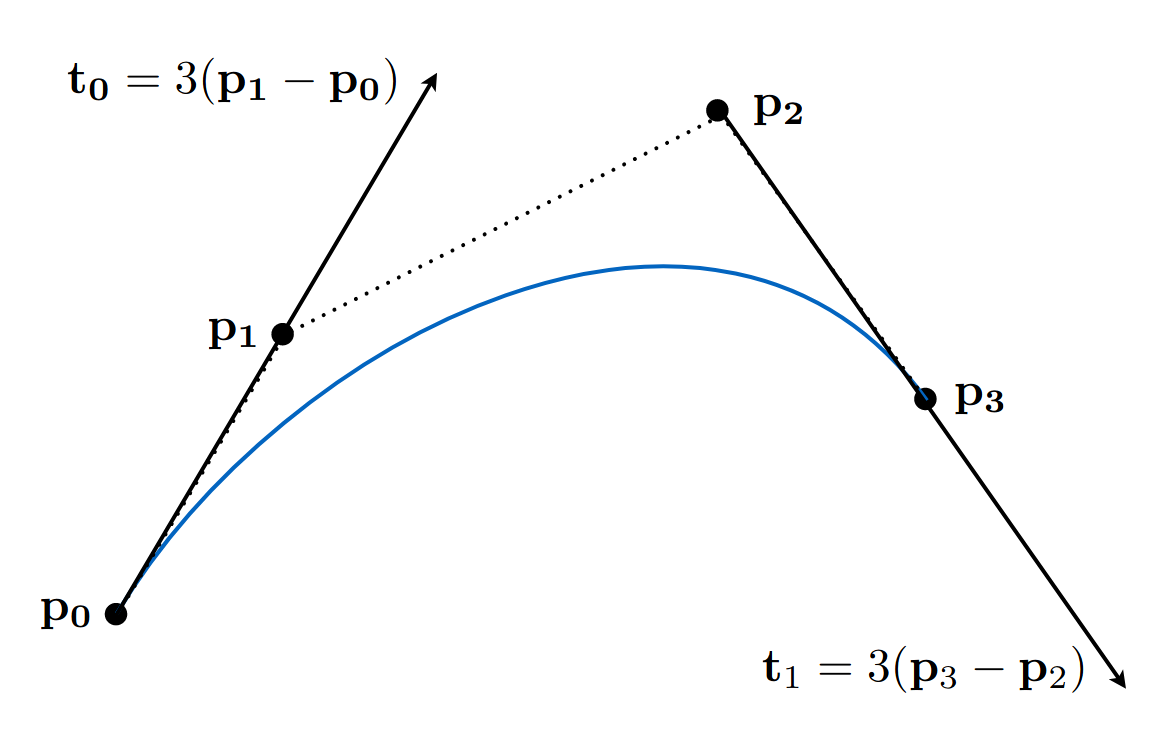
ae57ba9e08eb460eb5073c3d027d84a5.png

求导即可

Piecewise Bézier Curves

分段贝塞尔曲线

通常使用三次贝塞尔曲线

https://math.hws.edu/eck/cs424/notes2013/canvas/bezier.html

下面讨论连续性

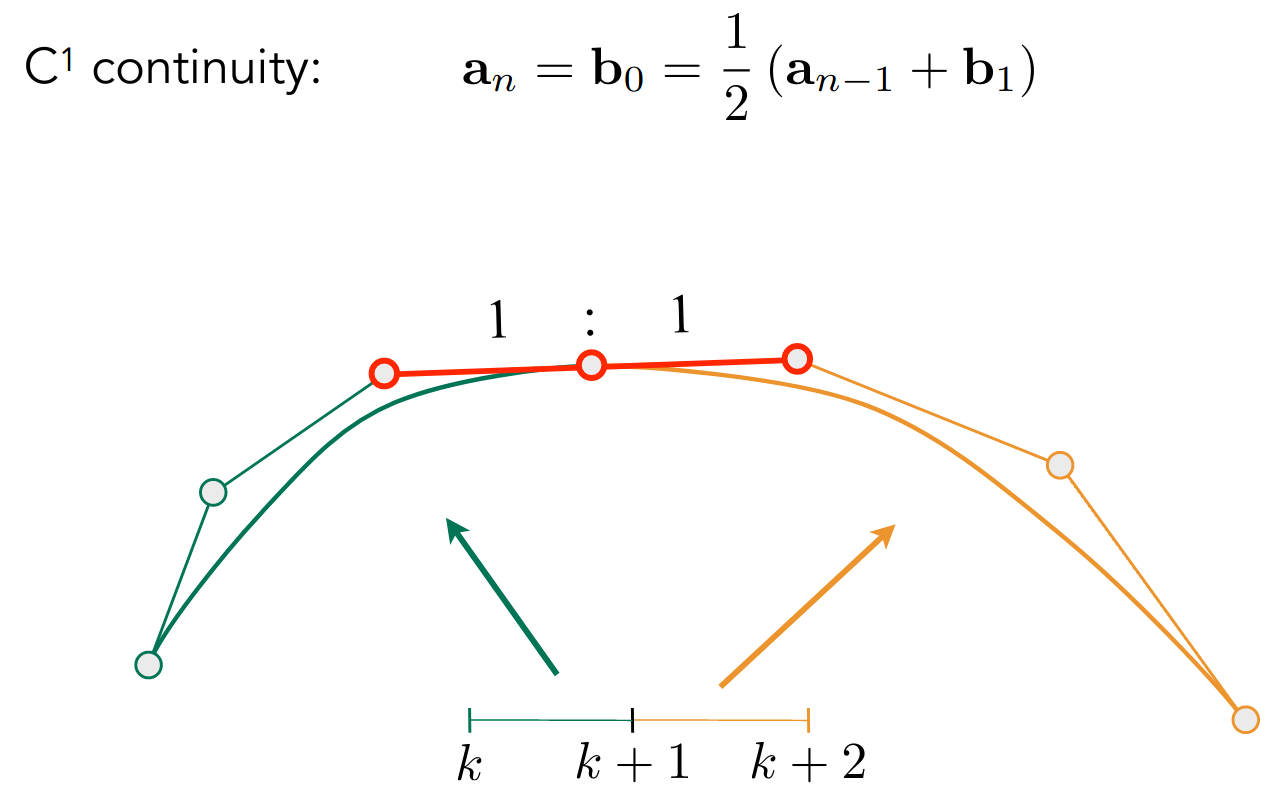
bc95b582f0bb464b9e1729a07df0b53b.png

Other types of splines

Bézier Curves 的超集

Surfaces

Bezier Surfaces

多引入一个参数

计算思路大致相同，只不过多一个维度

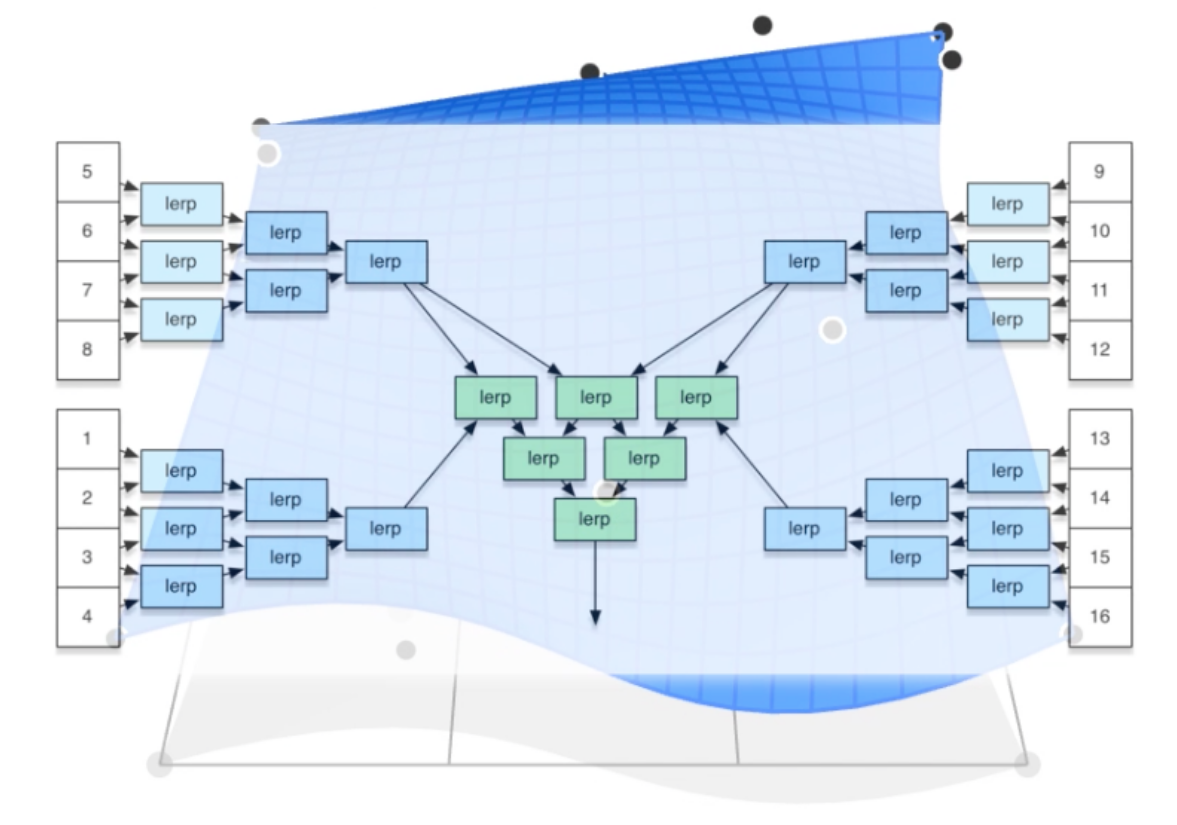
86a750f5e8f2451081f938fd19a2b750.png

Mesh Operations

处理曲面的多边形

2397ee06883045249e96a2bc16508d44.png

更多内容在下一节课

PA4

note

相当水

cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points,
                             float t) {
  // TODO: Implement de Casteljau's algorithm
  if (control_points.size() == 2) {
    return (1 - t) * control_points[0] + t * control_points[1];
  }


  std::vector<cv::Point2f> new_control_points;


  for (size_t i = 0; i < control_points.size() - 1; ++i) {
    new_control_points.emplace_back((1 - t) * control_points[i] +
                                    t * control_points[i + 1]);
  }


  return recursive_bezier(new_control_points, t);
}


void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) {
  // TODO: Iterate through all t = 0 to t = 1 with small steps, and call de
  // Casteljau's recursive Bezier algorithm.


  assert(control_points.size() == count);


  for (double t = 0.0; t <= 1.0; t += step) {
    auto point = recursive_bezier(control_points, t);


    window.at<cv::Vec3b>(point.y, point.x)[1] = 255; // green
  }
}

另外还实现了通用的 naive_bezier

使用了 C++17 中的 beta 函数计算二项展开系数

double binom(int n, int k) {
  return 1 / ((n + 1) * std::beta(n - k + 1, k + 1));
}


void naive_bezier(const std::vector<cv::Point2f> &points, cv::Mat &window) {
  assert(points.size() == count);


  for (double t = 0.0; t <= 1.0; t += step) {
    cv::Point2f point{};
    for (size_t i = 0; i < points.size(); ++i) {
      point += binom(count - 1, i) * std::pow(1 - t, count - 1 - i) *
               std::pow(t, i) * points[i];
    }


    window.at<cv::Vec3b>(point.y, point.x)[2] = 255; // blue
  }
}

需要修改 mouse_handler 和 main 中的控制点数量以实现任意阶的贝塞尔曲线

还有光栅化的时候坐标似乎不是整数

window.at<cv::Vec3b>(point.y, point.x)[1] = 255;

为什么 x 和 y 颠倒了

pic

五阶贝塞尔曲线

同时使用 bezier 和 naive_bezier 绘制

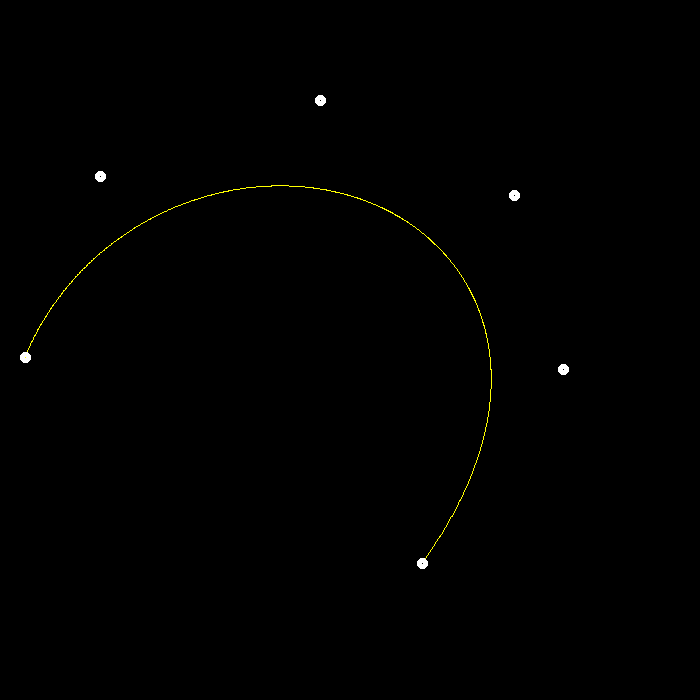
f9fbe0e6dda84b0ca34a8e459c0ccdcf.png

todo

几何（网格处理）、阴影图

Mesh Subdivision

Loop Subdivision

Loop 是人名

只对三角形面有效

分两步

对于新生成的顶点，根据下图分配权重

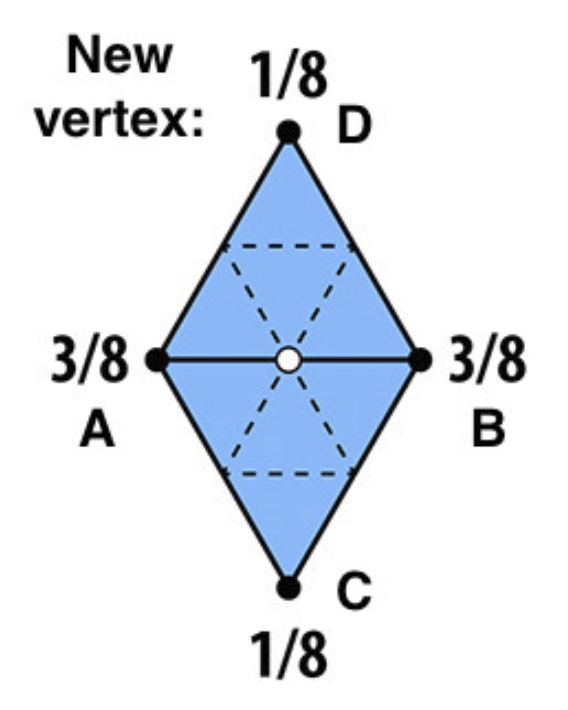
05471557b89442d990ce4651247dcac6.png

对于原本的顶点

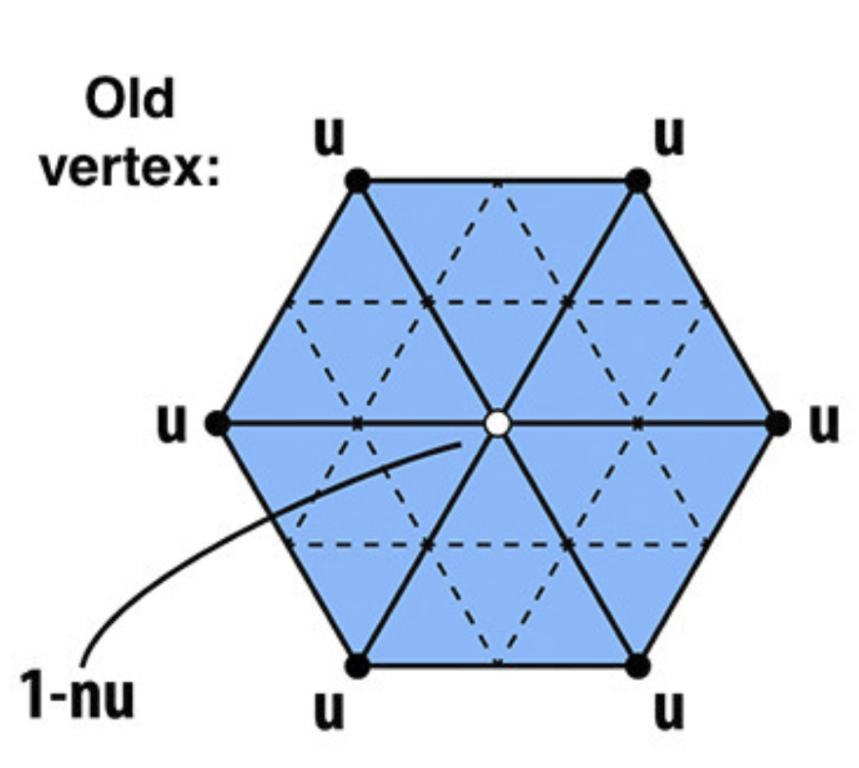
c568ceab134540558d6269bfaa257e09.png

需要得到该顶点的度 nn，然后根据 nn 设置权重 uu

u={316n=338notherwiseu=\begin{cases} \frac{3}{16} & n = 3 \newline \frac{3}{8n} & \text{otherwise}\end{cases}

这样可以保证当 nn 较小时，顶点自身的权重较大，而当 nn 较大时，顶点自身的权重较小

Catmull-Clark Subdivision

可用于任意多边形面

同样分两步走，首先看如何 split

第一步，在每个面的中心添加一个点，该点与这个面各边的中点相连

507a0a7ef9884130860a4a4492546a86.png

第一步过后，奇异点的数量会增加某个值，该值等于原图中非四边形面的数量

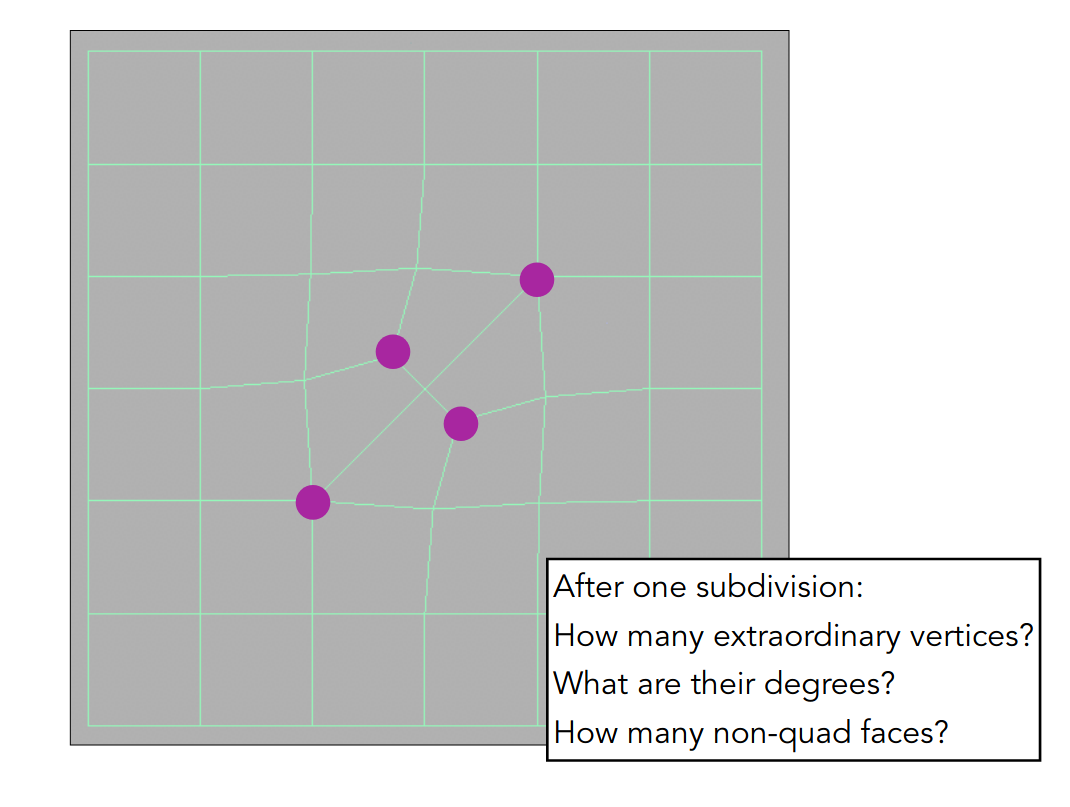
d3ed195faee94b52980494c28d0c25a8.png

之后重复上述操作，可以证明奇异点的数量不会改变

下面考虑权重问题，直接给出公式

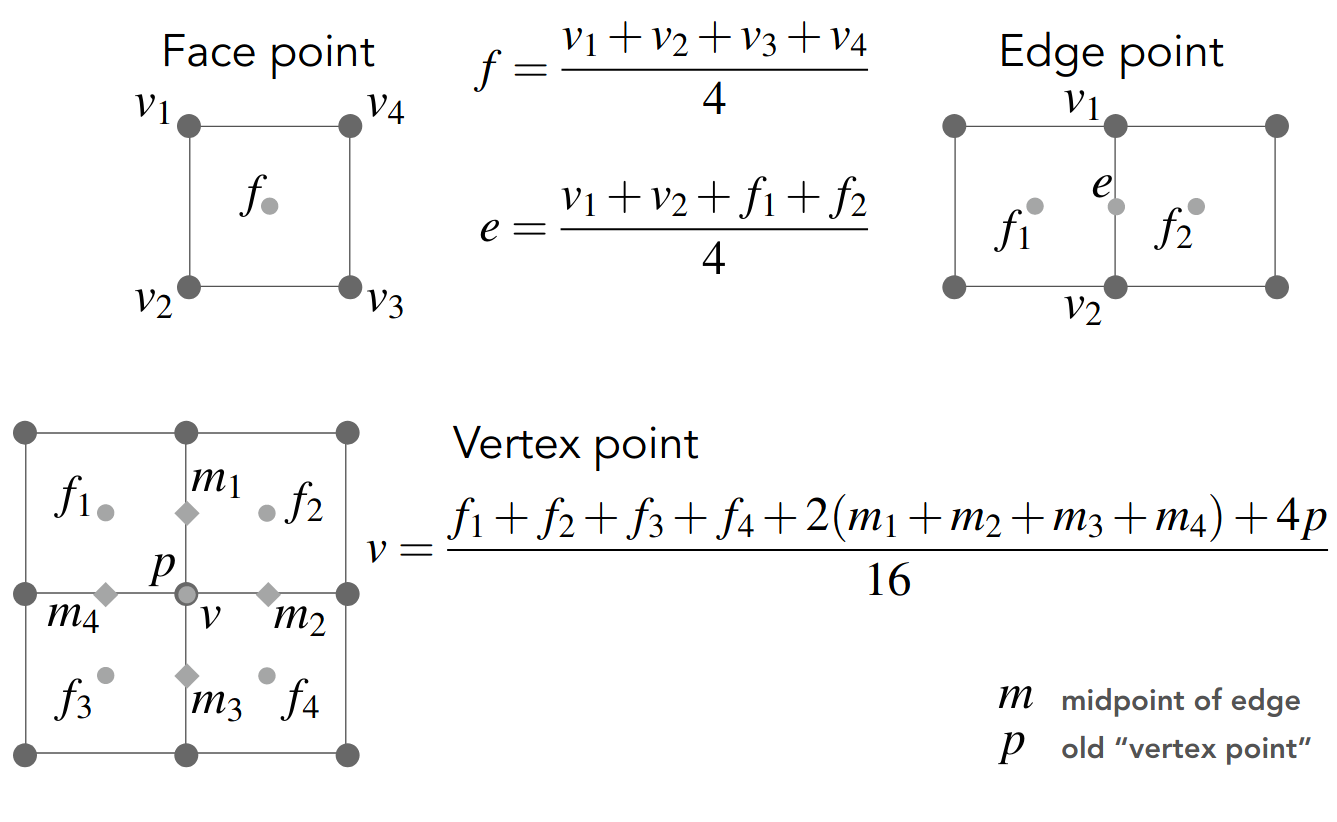
adc049dc812f4052aeae0134815fef93.png

Mesh Simplification

Suppose we simplify a mesh using edge collapsing

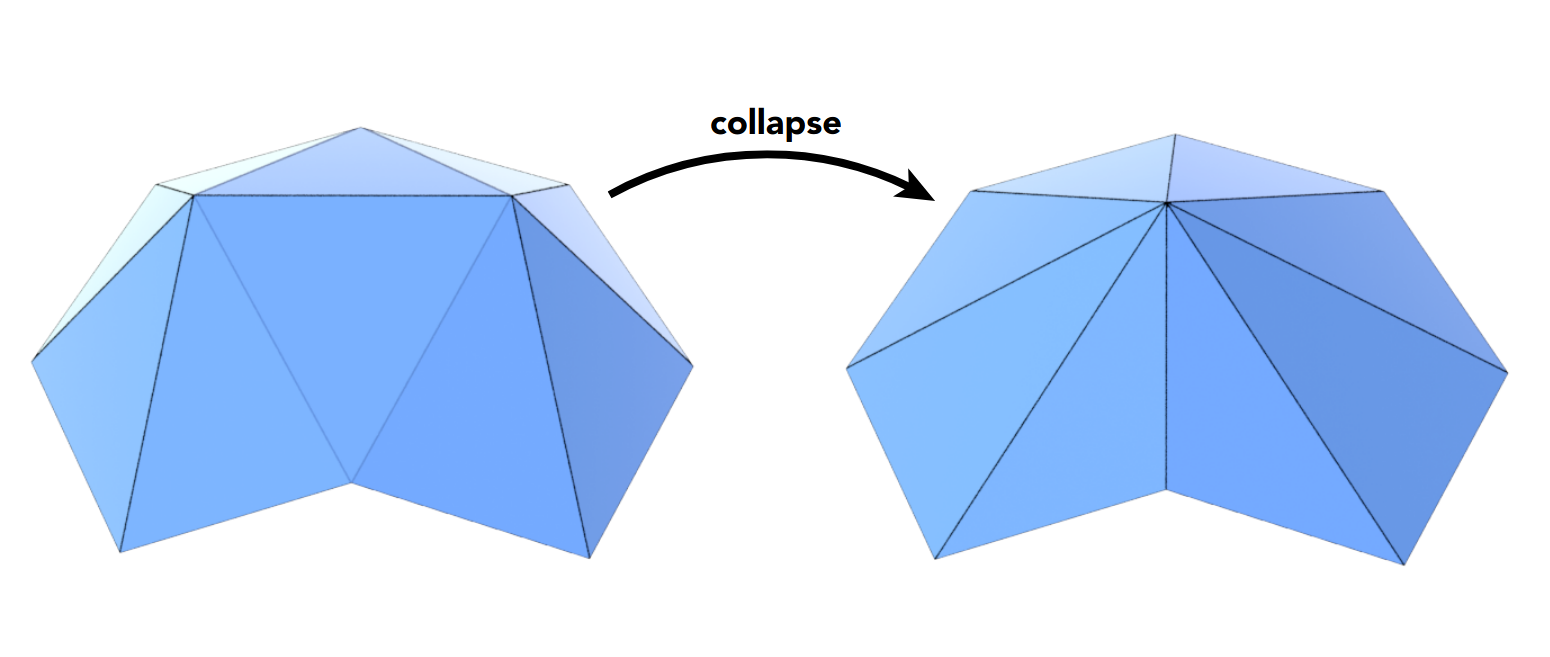
464305cb2b52471abe62fff24e41f2b2.png

相当于将一条边的两个端点变为一个点

为了计算变换的误差，需要引入二次误差度量

17bc6cfdf3f1416e84649605d44a6f59.png

也就是该点与原相邻面距离的平方和

对于曲面中的每一条边，都可以计算出对应二次误差度量的最小值

以从小到大的顺序进行 edge collapsing 即可

注意每进行一步 edge collapsing，可能需要重新计算某些边对应二次误差度量的最小值

本质上是贪心算法，不保证能找到最优解，不过实际中效果还不错

Shadow Mapping

光线追踪的导论

之前提过，光栅化的着色不考虑 shadow

现在考虑点光源产生的硬阴影

关键思想是 the points NOT in shadow must be seen both by the light and by the camera

所以着色要分为两轮

  1. 从点光源的方向看场景，进行深度测试，得到 Shadow Mapping
  2. 从相机的方向看场景，对于每一个点，反向应用 Shadow Mapping 得到点光源的方向的深度值，并进行比较

可见的情形

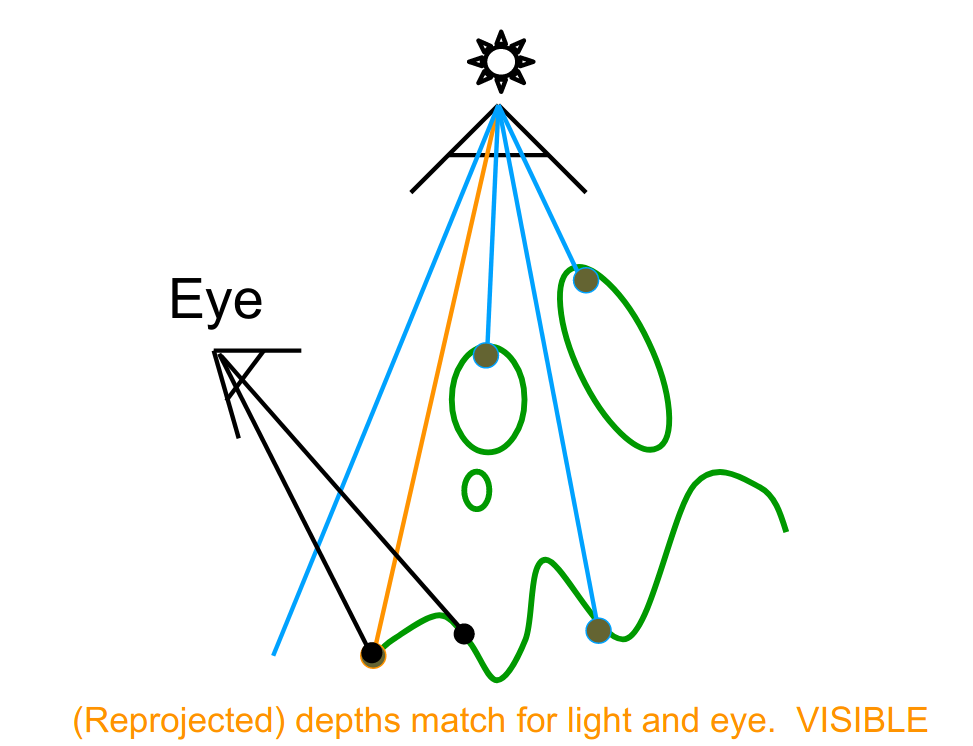
96fd09ce0863407b8731560818ad053d.png

不可见的情形

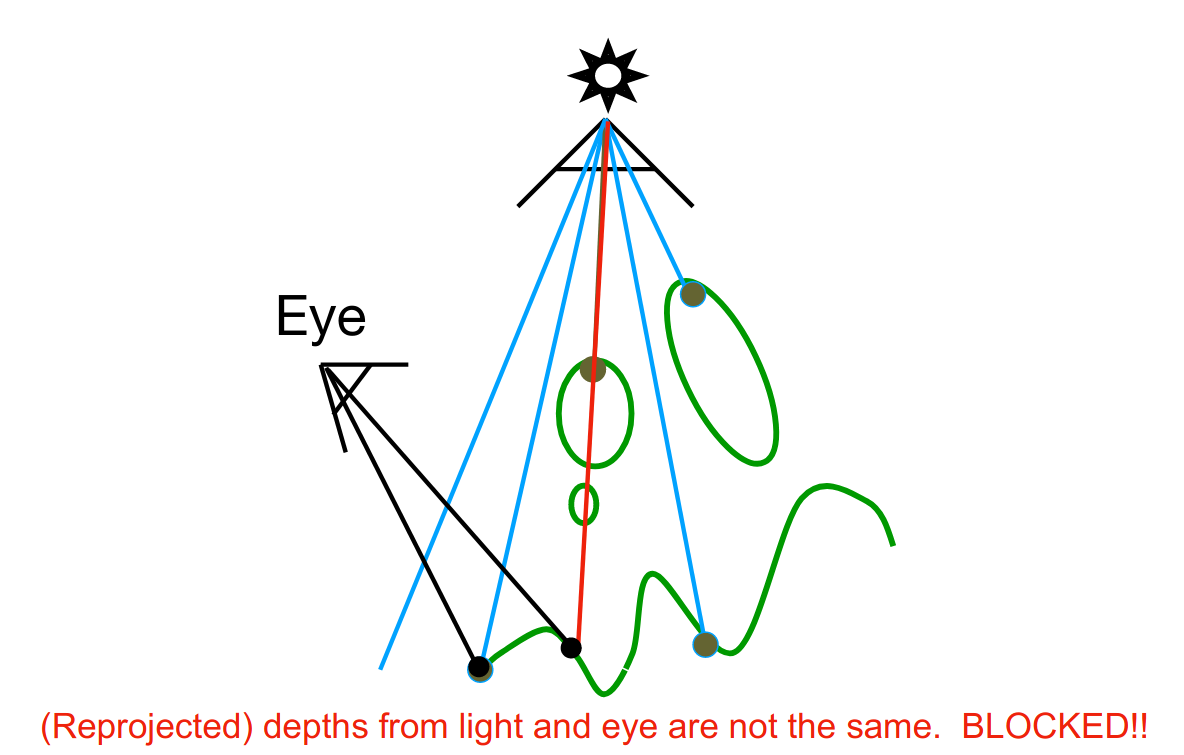
09cd451862c64b7fa810d66187734b7b.png

这种方法得到的 shadow 可能会出现走样，取决于 Shadow Mapping 的采样率

下面区分一下硬阴影和软阴影

cd1b1cc67cdc4f4abf0cc2c22b9bef57.png

软阴影中阴影的渐变效果，本质上是因为光源有一定的大小，而非点光源

光线追踪（基本原理）

Basic Ray-Tracing Algorithm

对光线的假设

  1. 光线沿直线传播
  2. 光线之间没有干扰
  3. 光路可逆

只要考虑到光线的反射和折射，并使用 Blinn-Phong reflectance model 叠加着色，就是最基本的光线追踪算法

Recursive (Whitted-Style) Ray Tracing

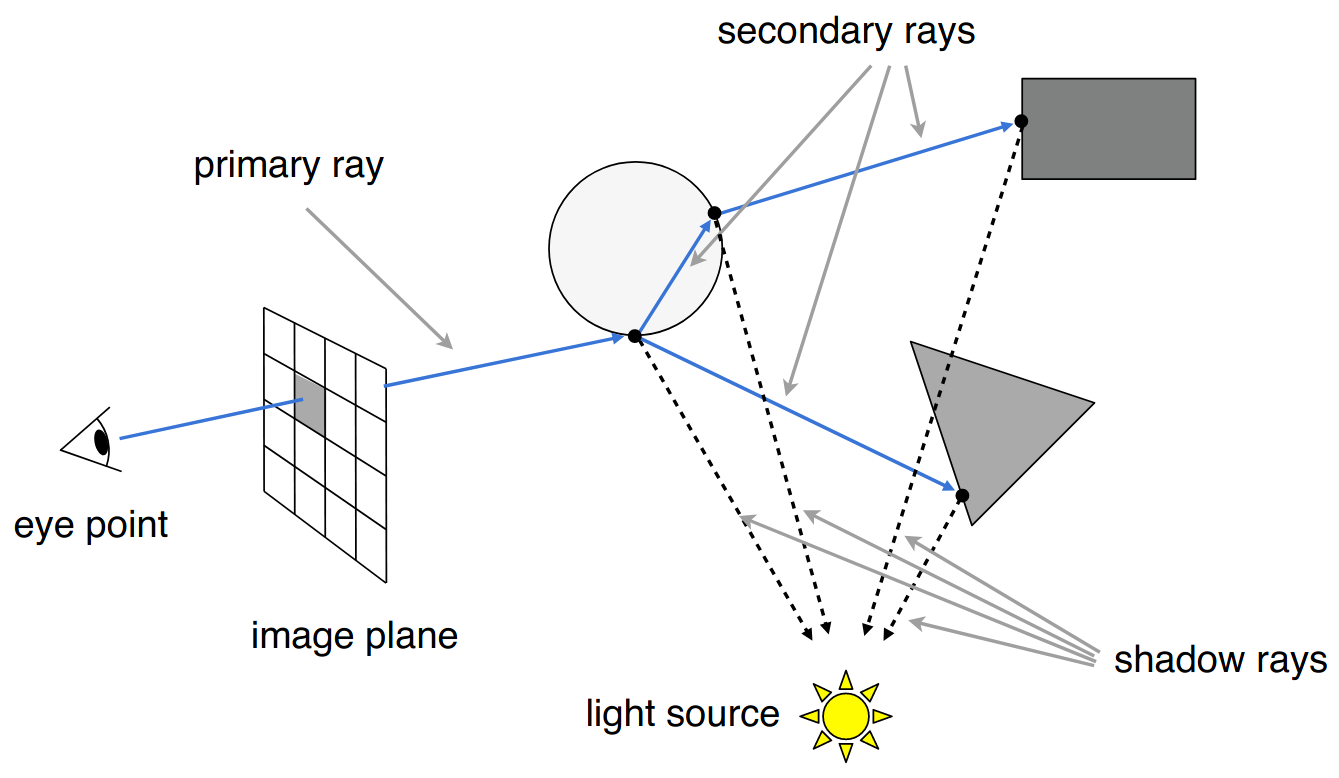
81d0817a16ee4b9e9800372f18ad9875.png

下面考虑一些技术细节

Ray-Surface Intersection

需要求出光线和几何表面的交点

首先需要为光线建模，实际上就是一条射线

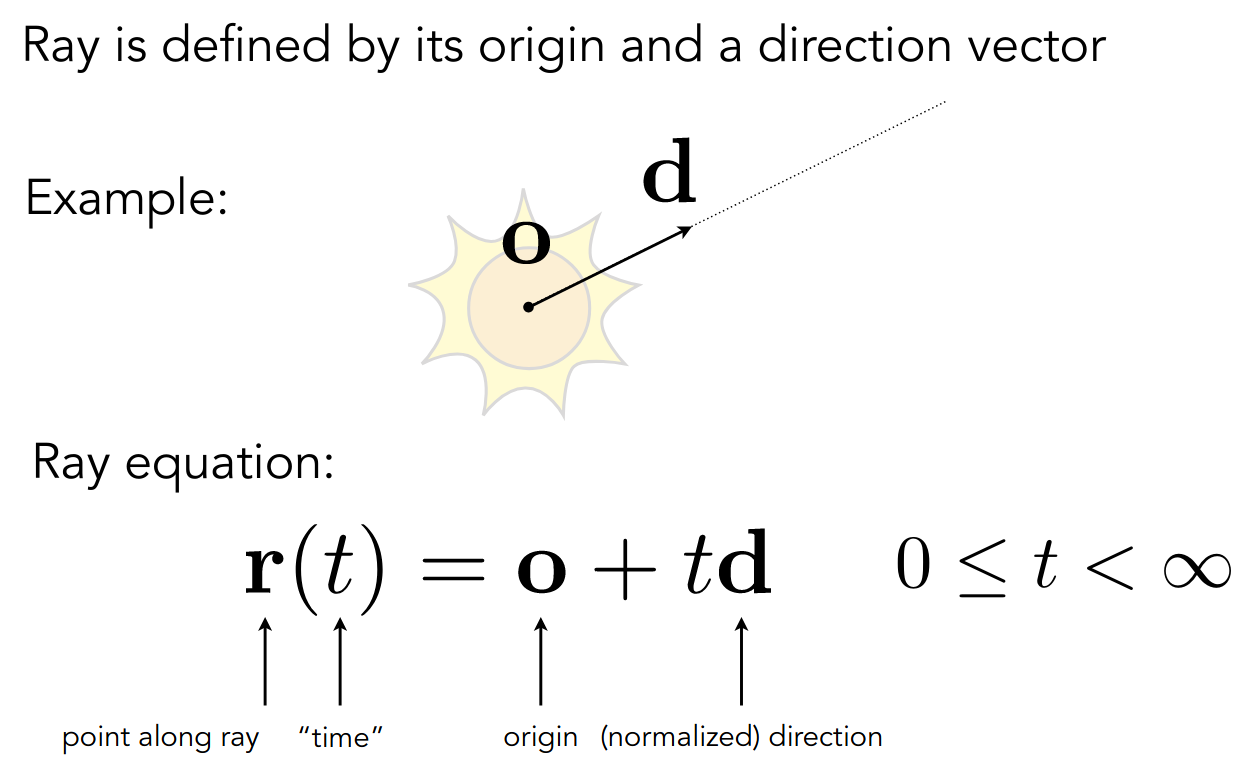
48696364e85f4a879f15ad15dabd1fca.png

Implicit Surfaces

以 Algebraic Surfaces 为例

只需要联立下面两式

r(t)=o+tdf(p)=0\begin{array}{l} r(t) = o + td \newline f(p) = 0 \end{array}

求出正实数解 tt 即可

Explicit Surfaces

以 Polygon Mesh 为例

首先考虑一个简单的算法，对光线和几何表面的每个三角形求交点

光线和三角形求交，实际上可以分解为

  1. 光线和平面求交
  2. 交点是否在三角形内（外积）

所以只要考虑光线和平面求交，使用点法式表示平面方程

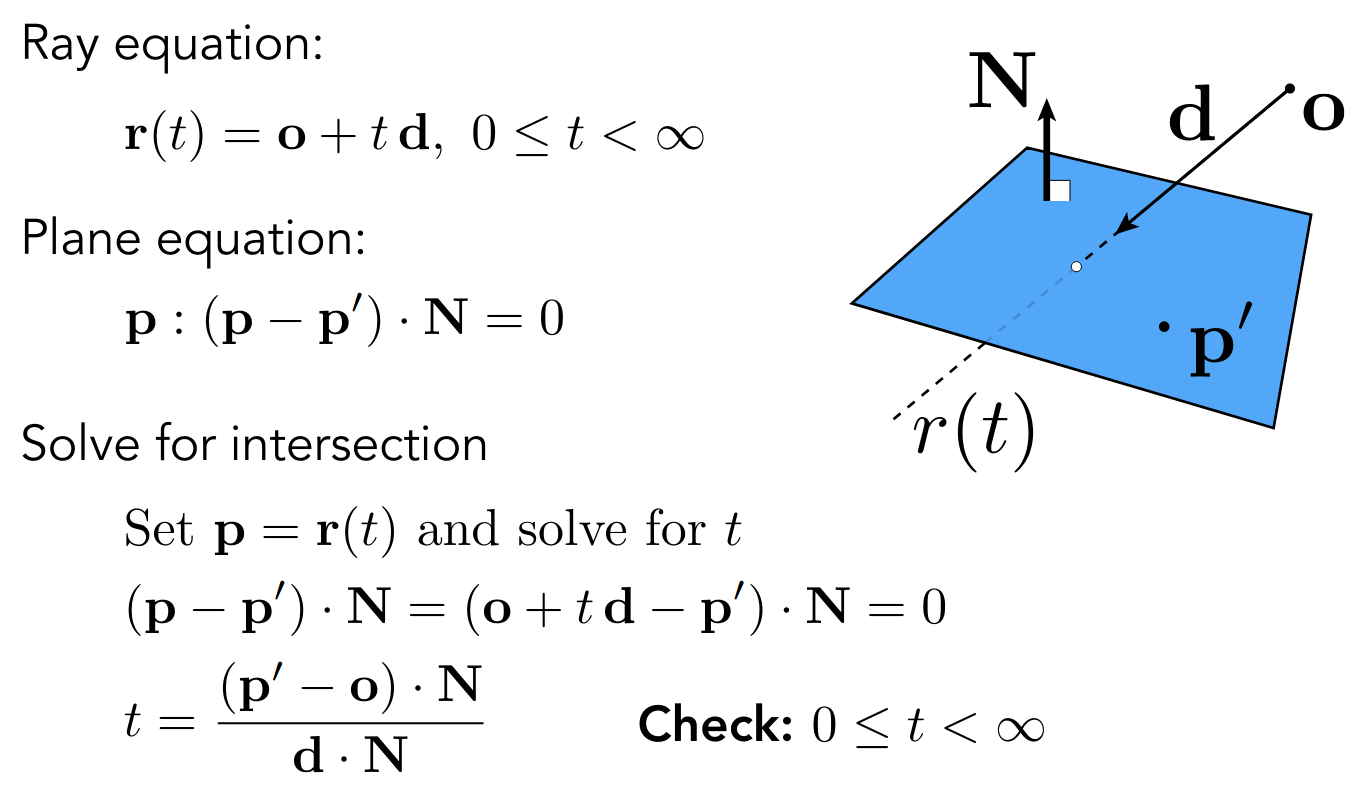
38c35a80432a4848a01a7977822c6d71.png

联立即可解出 tt

一个优化是直接考虑光线和三角形求交

即 Möller Trumbore Algorithm

4f7c4424312244e6888dcd1fb998d837.png

使用重心坐标表示交点 P^\hat{P}

向量的维度为 33

有三个未知量 t,b1,b2t,b_1,b_2

也就是一个线性方程组

Accelerating Ray-Surface Intersection

当场景中三角形数量较多时，或者像素点数量较多时

对光线和几何表面的每个三角形求交点，实际上至少需要计算这么多次

pixels x traingle x bounces

我们使用 Bounding Volumes 加速

Bounding Volumes

当光线和 Bounding Volumes 都不相交时，肯定不会与 Surface 相交

为了计算方便，我们使用 Axis-Aligned Bounding Box (AABB)

核心算法如下，我们视 Bounding Volumes 为三对平面相交的部分

7e8126aa678046f5883c625258c22c15.png

求出光线进入三对平面的 max\text{max} 和光线离开三对平面的 min\text{min}

即可得出光线在 Bounding Volumes 内部的时间段

满足如下两个条件

tenter<texittexit≥0\begin{array}{l} t_{\text{enter}} < t_{\text{exit}} \newline t_{\text{exit}} \ge 0 \end{array}

即可判定光线和 Bounding Volumes 相交

tenter<0t_{\text{enter}} \lt 0 也无所谓，代表光线源点在 Bounding Volumes 内部

而关于计算 tt，由于平面和坐标轴对齐，所以只考虑一个分量即可

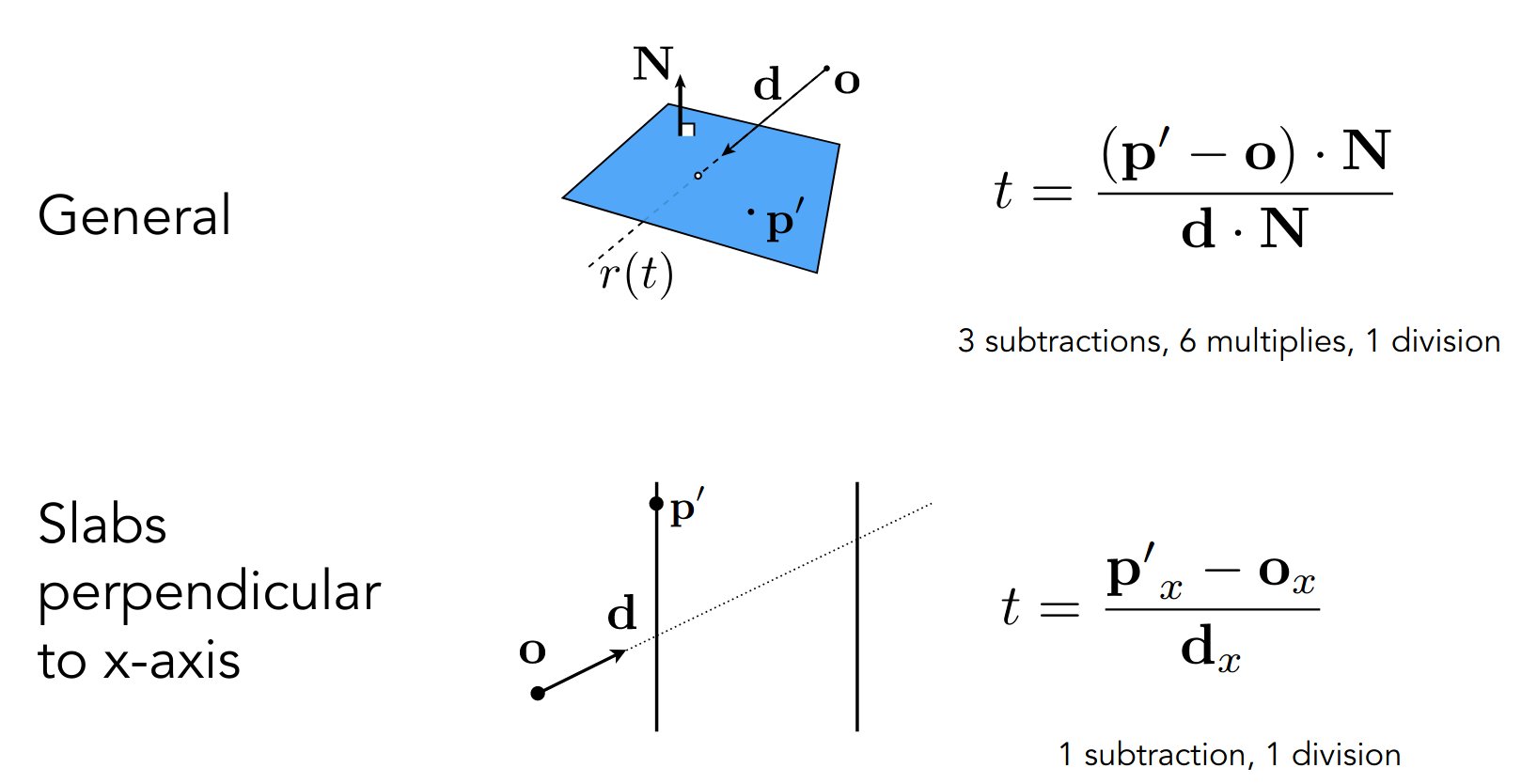
0ba3ff8677394d6b94842fa93d422b98.png

PA5

竟然没有使用任何第三方库……

Render

原理如下

https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-generating-camera-rays/generating-camera-rays

可能是因为相机朝向 -z 轴，所以计算 y 轴分量时需要取负

另外别忘了加上 0.5

  for (int j = 0; j < scene.height; ++j) {
    for (int i = 0; i < scene.width; ++i) {
      // generate primary ray direction
      float x;
      float y;
      // TODO: Find the x and y positions of the current pixel to get the
      // direction vector that passes through it. Also, don't forget to multiply
      // both of them with the variable *scale*, and x (horizontal) variable
      // with the *imageAspectRatio*
      x = (((i + 0.5) / (float)scene.width) * 2 - 1) * scale * imageAspectRatio;
      y = (1 - ((j + 0.5) / (float)scene.height * 2)) * scale;
      // y = (((j + 0.5) / (float)scene.height) * 2 - 1) * scale;


      Vector3f dir = normalize(
          Vector3f(x, y, -1)); // Don't forget to normalize this direction!
      framebuffer[m++] = castRay(eye_pos, dir, scene, 0);
    }
    UpdateProgress(j / (float)scene.height);
  }

本质上是映射

[0,width]×[0,height]→[−1,1]2[0, \text{width}] \times [0, \text{height}] \to [-1,1]^{2}

rayTriangleIntersect

v0,v1,v2v_0, v_1, v_2 是三角形的三个顶点

origorig 是光线的起点

dirdir 是光线单位化的方向向量

tnear,u,vtnear, u, v 是需要使用 Möller Trumbore Algorithm 来更新的参数

bool rayTriangleIntersect(const Vector3f &v0, const Vector3f &v1,
                          const Vector3f &v2, const Vector3f &orig,
                          const Vector3f &dir, float &tnear, float &u,
                          float &v) {
  // TODO: Implement this function that tests whether the triangle
  // that's specified bt v0, v1 and v2 intersects with the ray (whose
  // origin is *orig* and direction is *dir*)
  // Also don't forget to update tnear, u and v.
  Vector3f e1 = v1 - v0;
  Vector3f e2 = v2 - v0;
  Vector3f s = orig - v0;
  Vector3f s1 = crossProduct(dir, e2);
  Vector3f s2 = crossProduct(s, e1);


  float denominator = dotProduct(s1, e1);
  float _tnear = dotProduct(s2, e2) / denominator;
  float _u = dotProduct(s1, s) / denominator;
  float _v = dotProduct(s2, dir) / denominator;
  if (_tnear >= 0 and 0 <= _u and _u <= 1 and 0 <= _v and _v <= 1 and
      _u + _v <= 1) {
    tnear = _tnear;
    u = _u;
    v = _v;
    return true;
  }


  return false;
}

直接抄公式即可

注意限制条件

pic

1636a08aa69a487f8d2e4a5a3cd6e76c.png

使用 imagemagick 转换 ppm 为 png

$ convert pa5.ppm pa5.png

光线追踪（加速结构）

上节课讲了如何计算光线和 Bounding Volumes 求交

这节课介绍如何利用 Bounding Volumes 加速光线和几何表面求交

以二维为例

Uniform Spatial Partitions (Grids)

首先需要将场景进行划分，进行预处理

考虑均匀划分

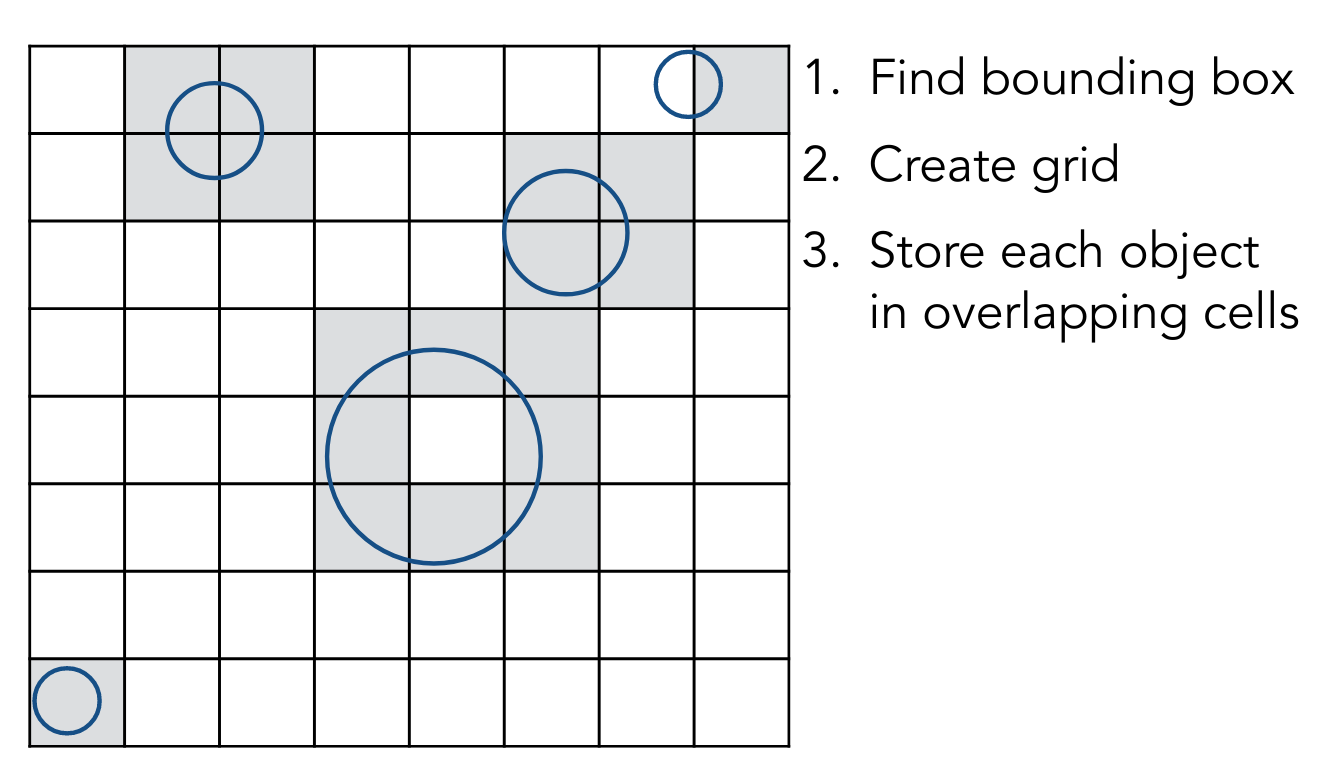
2e39fa2fe6274a478c37a468c4f2be9a.png

然后让光线与 grid 求交，若相交，且内部有物体，再去和物体求交

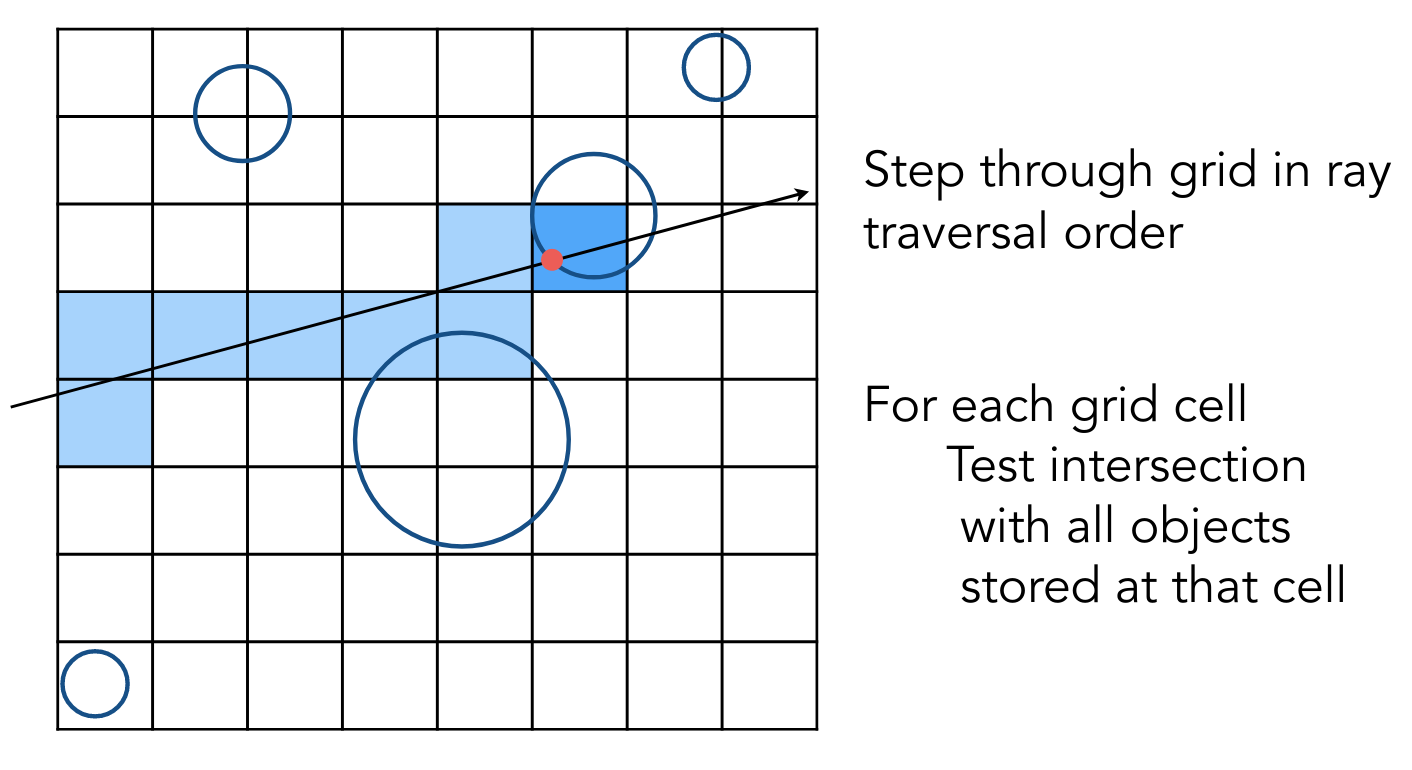
e0abe0d1292d48f99a986cb0b7c47ab6.png

光线进行 grid traversal 时，不必考虑所有的 grids

以图中的方向为例，只需要考虑右面和上面的 grid 即可

类似画一条直线，参见 PA1 rasterizer.cpp 中的 draw_line 函数

Bresenham’s line drawing algorithm

对于 grid 的分辨率，若太大，起不到加速效果，若太小，光线与 grid 求交的开销太大

有经验规则

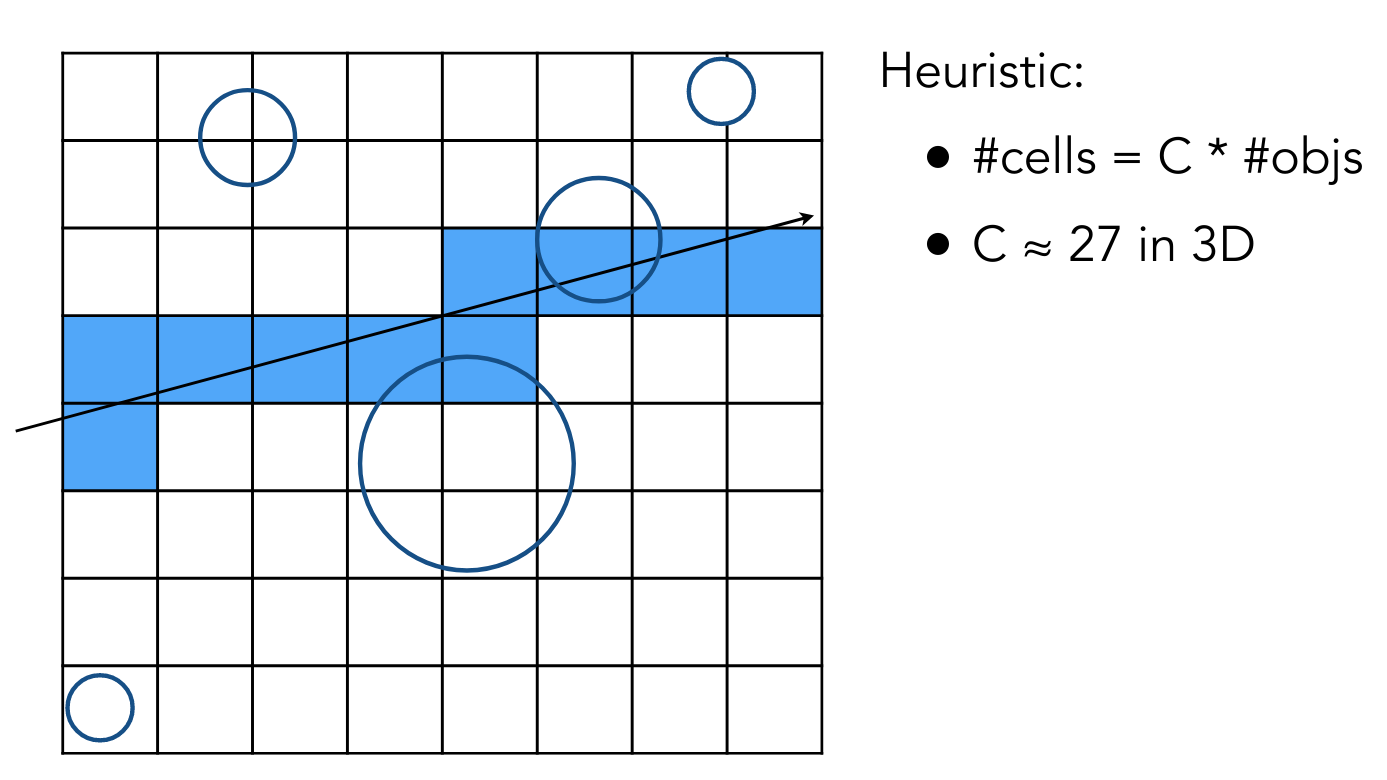
d03541b958834a708112382b352ed24b.png

然而，均匀划分对于物体不均匀分布的场景而言效果并不好

Spatial Partitions

考虑场景的不均匀划分

以 KD-Tree 为例，region 构成一个二叉树

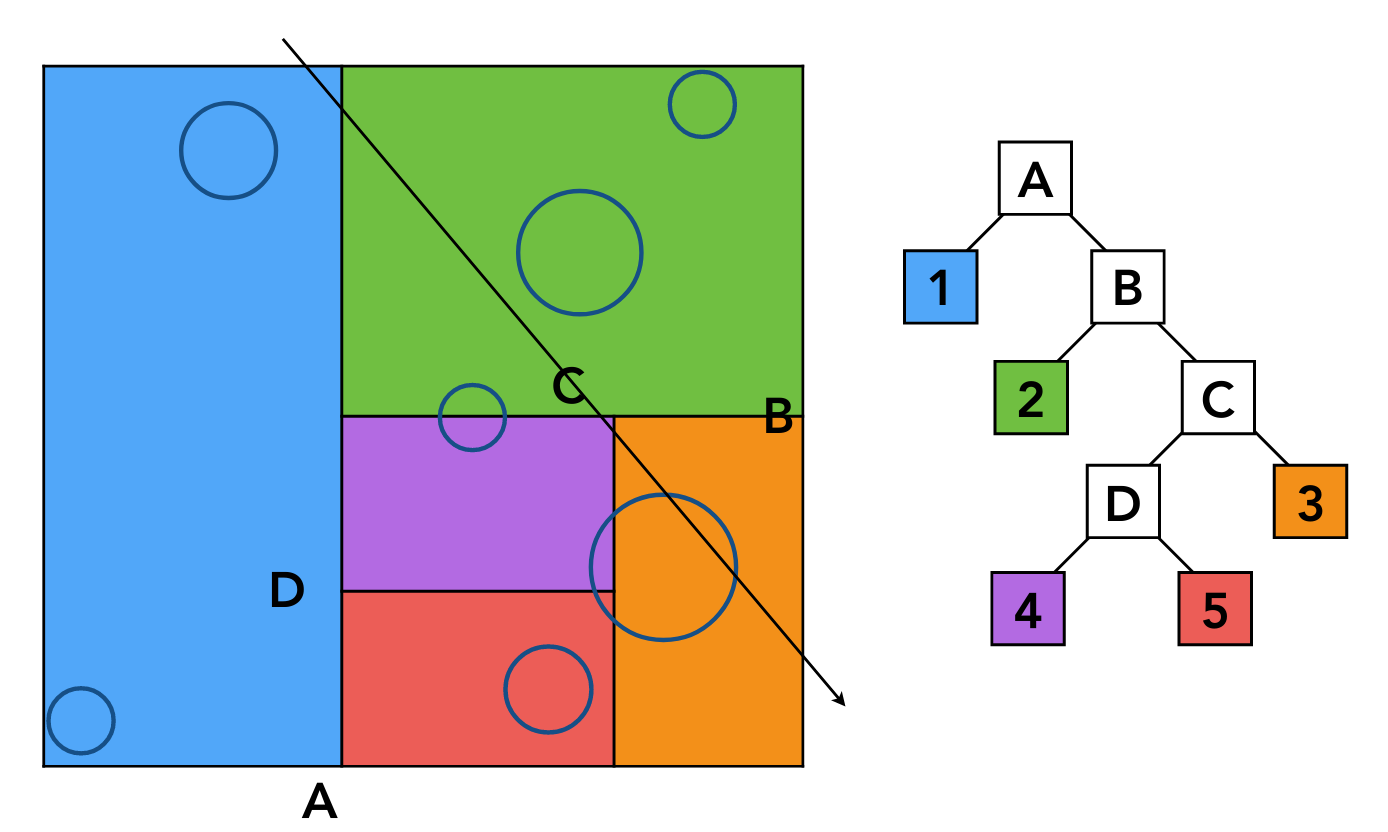
f86fb423e271469d8392a26710acde3e.png

需要注意，叶子节点需要根据 region 计算哪些物体在其内部，这并不容易

并且物体可能同时在不同的 region 中

Object Partitions & Bounding Volume Hierarchy (BVH)

考虑物体的不均匀划分

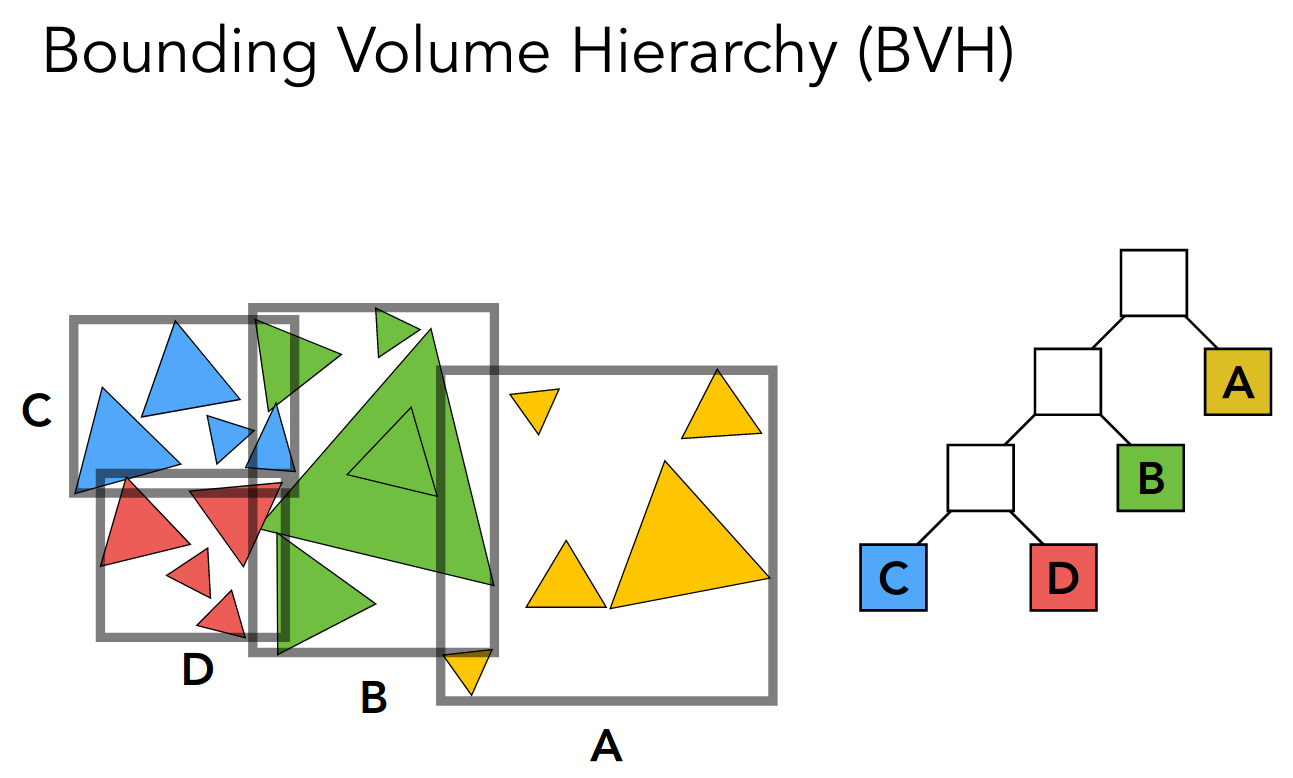
46f17663d6b040ae82698a28d73c4638.png

注意 Bounding Volumes 之间可能有重叠

每一次划分后，都需要重新计算子结构的 Bounding Volumes

而对于物体的划分，可以根据某个方向取中位数

总结一下求交的算法

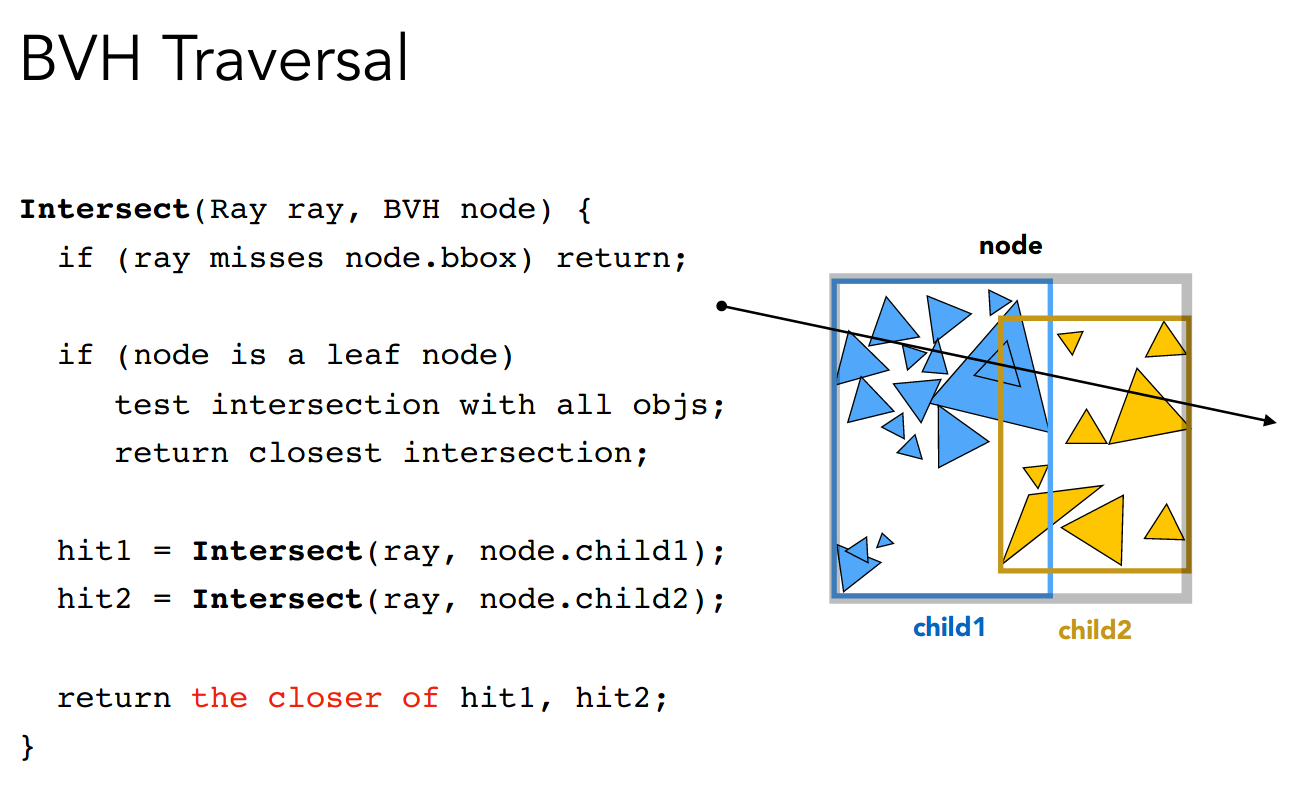
e8973027578d4989918f9e04710a16ff.png

综合了

区分一下上述两种不均匀划分

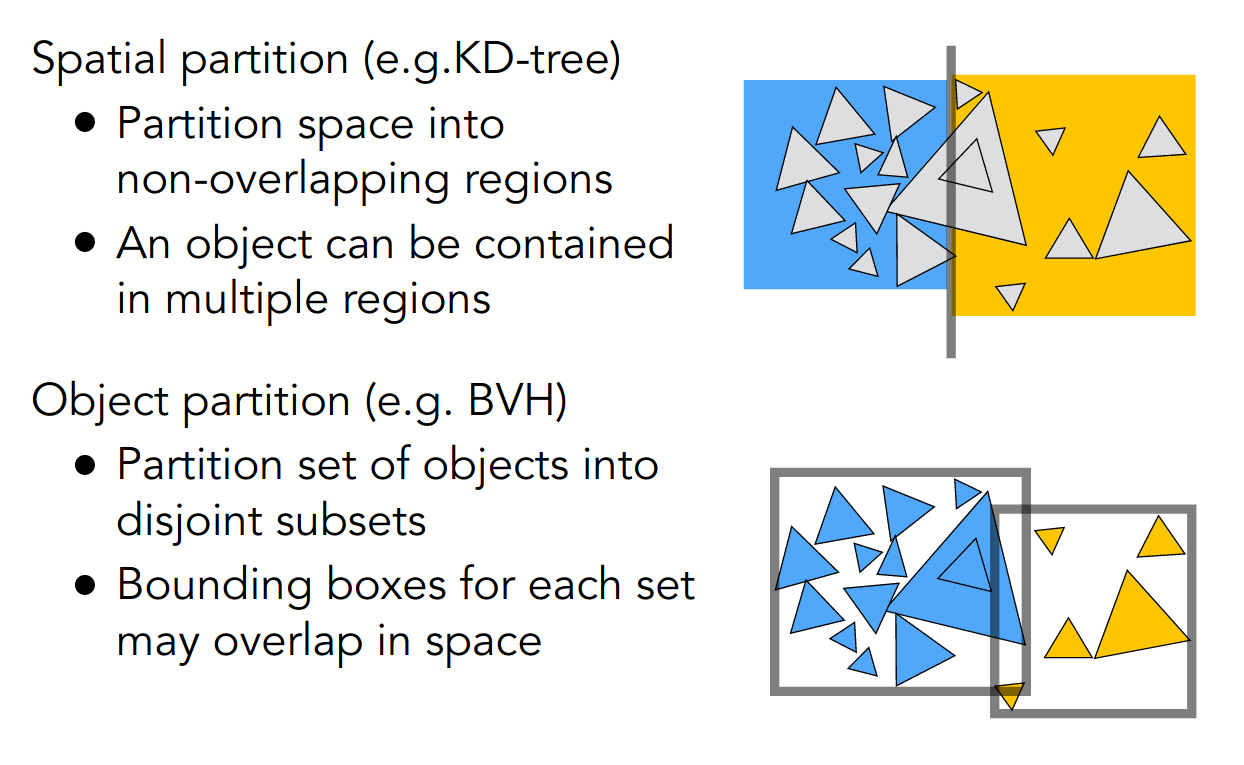
9eea1abb75314394824a8724f2a7f14b.png

至此，Recursive (Whitted-Style) Ray Tracing 基本上就介绍完了

Basic Radiometry

进入辐射度量学这个新的话题

我们需要对光的空间特性进行更精确的度量

首先引入几个概念

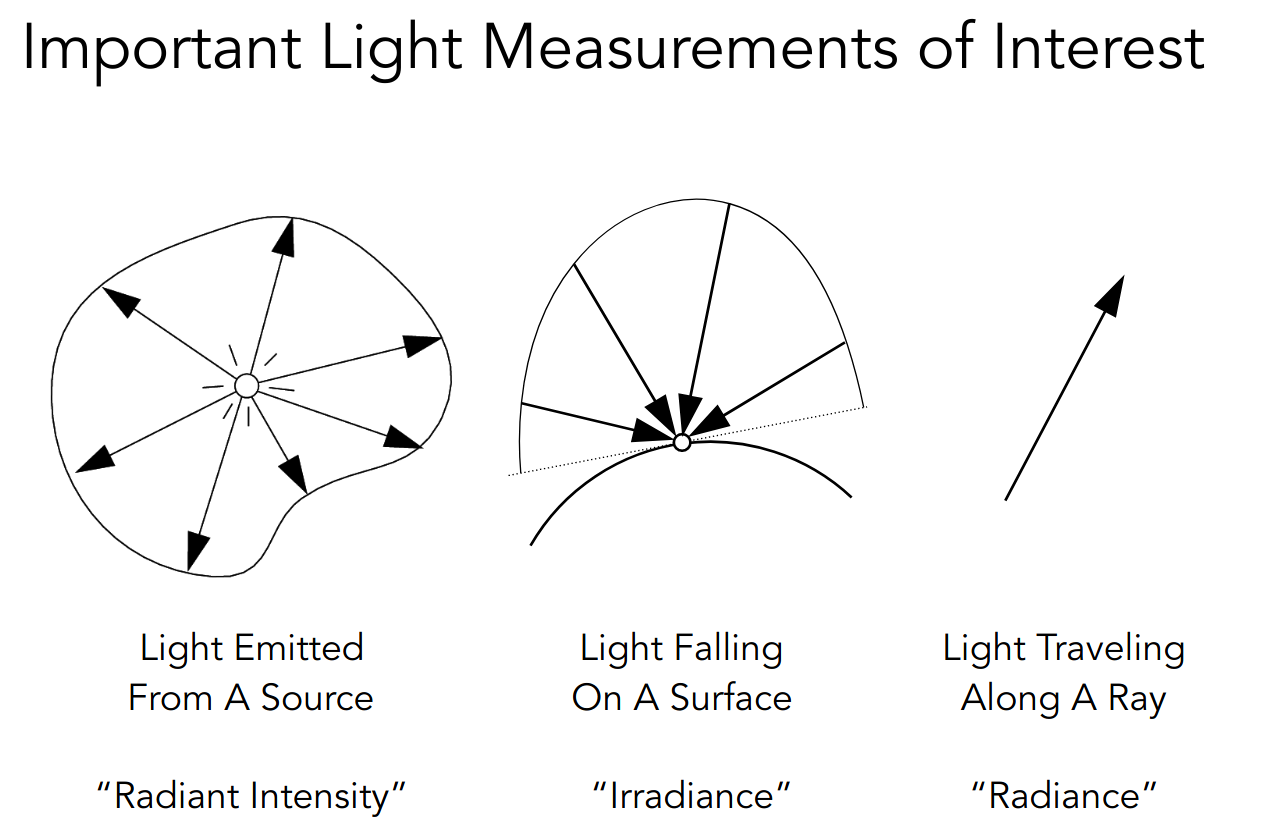
70a8153abfeb4bba8478568641d6eea5.png

Radiant Energy

能量 - 焦耳

Q[J=Joule]Q[\text{J=Joule}]

Radiant Flux (Power)

功率/辐射通量 - 瓦特/流明

Φ≡dQdt[W=Watt][lm=lumen]\Phi \equiv \frac{dQ}{dt} [\text{W=Watt}] [\text{lm=lumen}]

Radiant Intensity

辐射强度 - 坎德拉

I(ω)≡dΦ(ω)dω[Wsr][lmsr=cd=candela]I(\omega) \equiv \frac{d\Phi(\omega)}{d\omega} [\frac{\text{W}}{\text{sr}}] [\frac{\text{lm}}{\text{sr}}=\text{cd}=\text{candela}]

其中 ω\omega 为立体角

1142869ea8bc47469e92c1a2334e3d8f.png

加上微分符号就是微分立体角，即球面空间中一个方向上的单位立体角

使用球坐标系易知

dω=dAr2=sin⁡θdθdϕd\omega = \frac{dA}{r^2} = \sin \theta d\theta d\phi
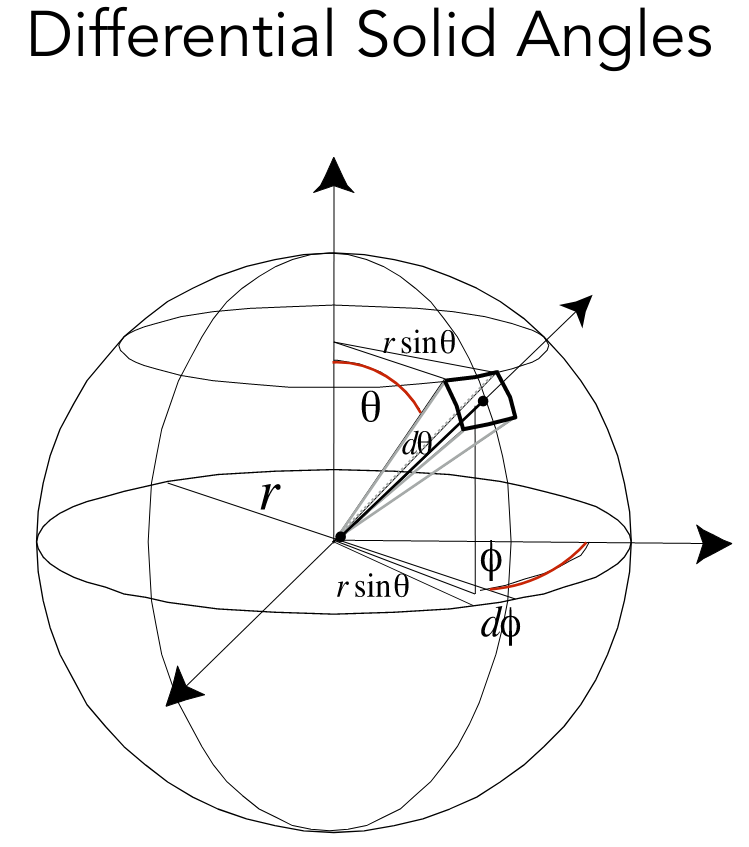
a1ff80d89bc54469b80f21d43429076e.png

于是 Radiant Flux 和 Radiant Intensity 有关系

Φ=∫S2Idω=4πI\Phi = \int_{S^2} I d\omega = 4\pi I

PA6

使用 Bounding Volumes 加速光线追踪

migration

首先需要将 PA5 的代码迁移过来

PA6 抽象出了 Scene 类和 Ray 类

castRay 的调用方式有所改变

  for (uint32_t j = 0; j < scene.height; ++j) {
    for (uint32_t i = 0; i < scene.width; ++i) {
      // generate primary ray direction
      float x =
          (2 * (i + 0.5) / (float)scene.width - 1) * imageAspectRatio * scale;
      float y = (1 - 2 * (j + 0.5) / (float)scene.height) * scale;
      // TODO: Find the x and y positions of the current pixel to get the
      // direction vector that passes through it.
      // Also, don't forget to multiply both of them with the variable
      // *scale*, and x (horizontal) variable with the *imageAspectRatio*


      Vector3f dir = normalize(
          Vector3f(x, y, -1)); // Don't forget to normalize this direction!
      framebuffer[m++] = scene.castRay(Ray{eye_pos, dir}, 0);
    }
    UpdateProgress(j / (float)scene.height);
  }

然后需要修改 Triangle.hpp 中的 getIntersection

inline Intersection Triangle::getIntersection(Ray ray) {
  Intersection inter;


  if (dotProduct(ray.direction, normal) > 0)
    return inter;
  double u, v, t_tmp = 0;
  Vector3f pvec = crossProduct(ray.direction, e2); // s1
  double det = dotProduct(e1, pvec);
  if (fabs(det) < EPSILON)
    return inter;


  double det_inv = 1. / det;
  Vector3f tvec = ray.origin - v0; // s
  u = dotProduct(tvec, pvec) * det_inv;
  if (u < 0 || u > 1)
    return inter;
  Vector3f qvec = crossProduct(tvec, e1); // s2
  v = dotProduct(ray.direction, qvec) * det_inv;
  if (v < 0 || u + v > 1)
    return inter;
  t_tmp = dotProduct(e2, qvec) * det_inv;


  // TODO find ray triangle intersection
  if (t_tmp < 0)
    return inter;


  inter.happened = true;
  inter.coords = ray(t_tmp);
  inter.distance = std::min(inter.distance, t_tmp); // dir is normalized
  // assume
  inter.normal = normal;
  inter.obj = (Object *)this;
  inter.m = m;


  return inter;
}

Triangle 类和 MeshTriangle 类 override 掉 getIntersection 方法

但是 MeshTriangle 类的实现和 Triangle 类的实现并不一致

MeshTriangle 类需要调用 BVHAccel::Intersect

可能是因为 Triangle 类代表了 Implicit Surfaces，而 MeshTriangle 类代表了 Explicit Surfaces

还有一些奇怪的 intersect 方法，似乎并没有被使用

Bounds3::IntersectP

然后实现光线和 Bounding Volumes 求交

inline bool Bounds3::IntersectP(const Ray &ray, const Vector3f &invDir,
                                const std::array<int, 3> &dirIsNeg) const {
  // invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z),
  // use this because Multiply is faster that Division
  // dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)],
  // use this to simplify your logic


  // TODO test if ray bound intersects
  double tx_min = (pMin.x - ray.origin.x) * invDir.x;
  double tx_max = (pMax.x - ray.origin.x) * invDir.x;
  if (tx_min > tx_max)
    std::swap(tx_min, tx_max);


  double ty_min = (pMin.y - ray.origin.y) * invDir.y;
  double ty_max = (pMax.y - ray.origin.y) * invDir.y;
  if (ty_min > ty_max)
    std::swap(ty_min, ty_max);


  double tz_min = (pMin.z - ray.origin.z) * invDir.z;
  double tz_max = (pMax.z - ray.origin.z) * invDir.z;
  if (tz_min > tz_max)
    std::swap(tz_min, tz_max);


  double t_enter = std::max({tx_min, ty_min, tz_min});
  double t_exit = std::min({tx_max, ty_max, tz_max});


  return t_enter < t_exit && t_exit >= 0;
}

由于平面是和坐标轴是平行的，所以 Bounds3 类中存储了三对平面的某个轴的坐标

例如平行于 yz 平面的平面只需要存储 x 坐标

另外需要保证 tmin≤tmaxt_{min} \le t_{max}

并没有使用 dirIsNeg 参数

BVHAccel::getIntersection

最后实现利用加速结构的求交的算法

Intersection BVHAccel::getIntersection(BVHBuildNode *node,
                                       const Ray &ray) const {
  // TODO Traverse the BVH to find intersection
  if (!node->bounds.IntersectP(
          ray, ray.direction_inv,
          std::array<int, 3>{static_cast<int>(ray.direction.x > 0),
                             static_cast<int>(ray.direction.y > 0),
                             static_cast<int>(ray.direction.z > 0)})) {
    return Intersection{};
  }


  // leaf node
  if (!node->left and !node->right) {
    return node->object->getIntersection(ray); // one object
  }


  assert(node->left and node->right);


  Intersection l_isect = getIntersection(node->left, ray);
  Intersection r_lsect = getIntersection(node->right, ray);


  return (l_isect.distance < r_lsect.distance) ? l_isect : r_lsect;
}

注意到每个叶子节点，也就是每个 Bounding Volume 中只有一个物体

可以通过 BVHAccel::recursiveBuild 观察建立 BVH 的细节

总结一下调用轨迹

  1. Scene::castRay
  2. Scene::intersect
  3. BVHAccel::Intersect
  4. BVHAccel::getIntersection
  5. Bounds3::IntersectP

pic

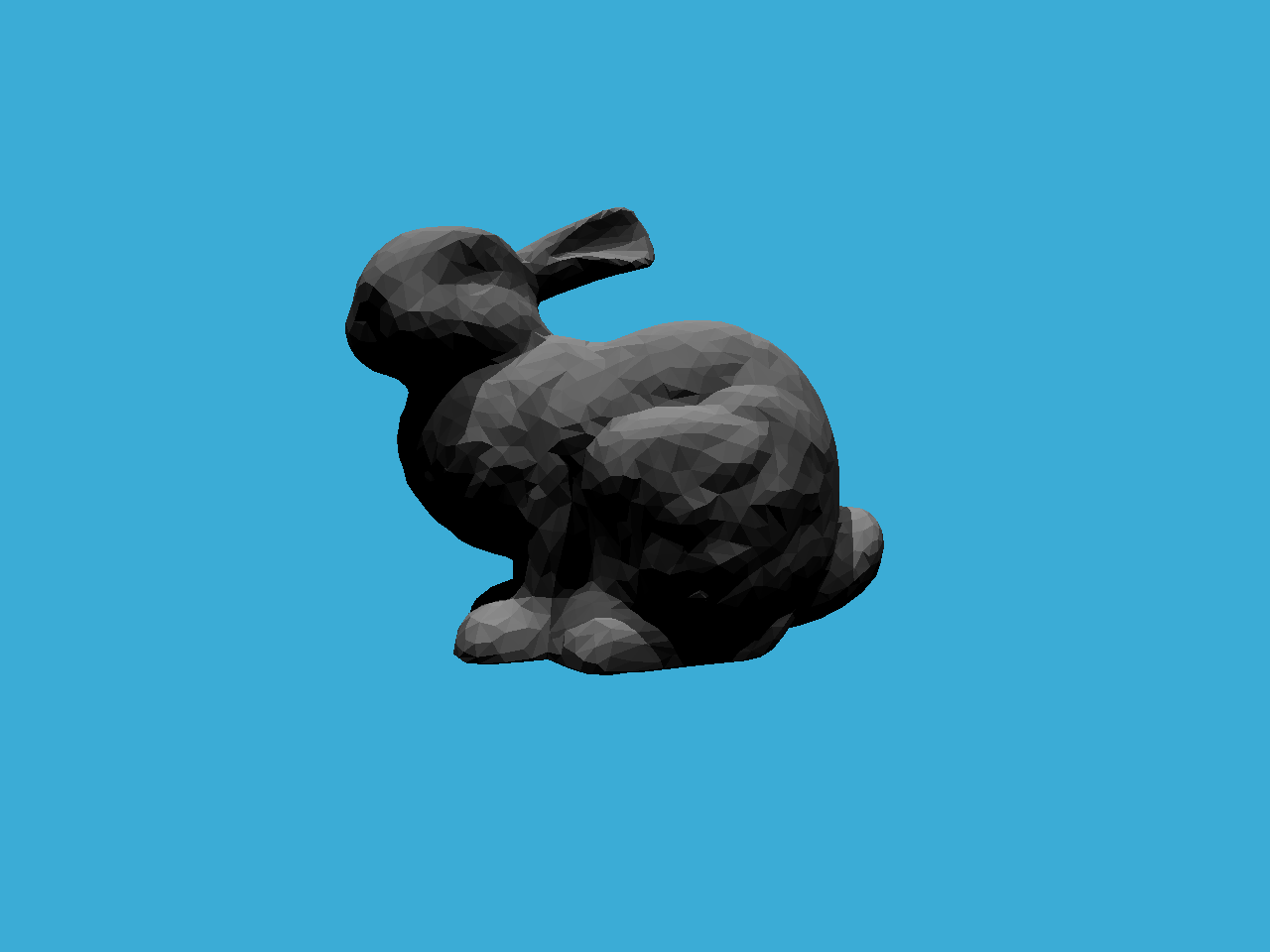
4cd18b6a9acd4c23a5ccad2057186c95.png

todo

光线追踪（辐射度量学、渲染方程与全局光照）

Basic Radiometry

接着上节课的内容

Irradiance

辐射照度 - 勒克斯

E(p)≡dΦ(p)dA[Wm2][lmm2=lux]E(p) \equiv \frac{d \Phi (p)}{dA } [\frac{\text{W}}{\text{m}^2}] [\frac{\text{lm}}{\text{m}^2}=\text{lux}]

注意这里的面积是投影面积

Radiance

辐射亮度

比 Irradiance 相比多了一个方向

比 Intensity 相比多了一个面积

power per unit solid angle per projected unit area

L(p,ω)≡d2Φ(p,ω)dωdAcos⁡θL(p,\omega) \equiv \frac{d^2 \Phi (p,\omega)}{d \omega dA \cos \theta}

请关注如下的关系

于是有

L(p,ω)=dE(p)dωcos⁡θ=dI(ω)dAcos⁡θL(p,\omega) = \frac{dE(p)}{d \omega \cos \theta} = \frac{dI(\omega)}{dA \cos \theta}

Bidirectional Reflectance Distribution Function (BRDF)

本质上是一个比例

RadianceIrradiance\frac{\text{Radiance}}{\text{Irradiance}}

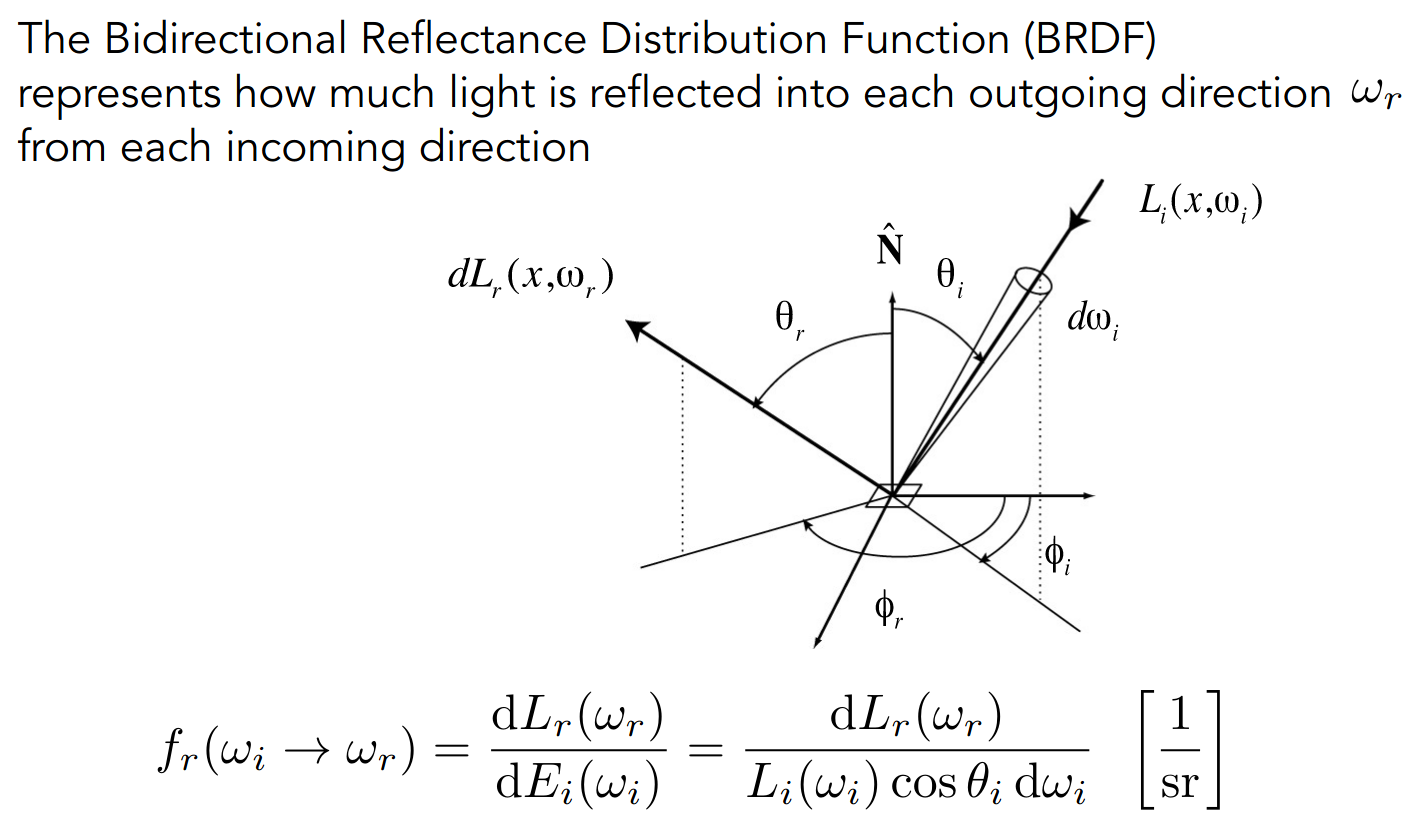
c768aac5919b42e7bbfd3f69e8e029e2.png

The Reflection Equation

对半球面所有可能的方向积分即可

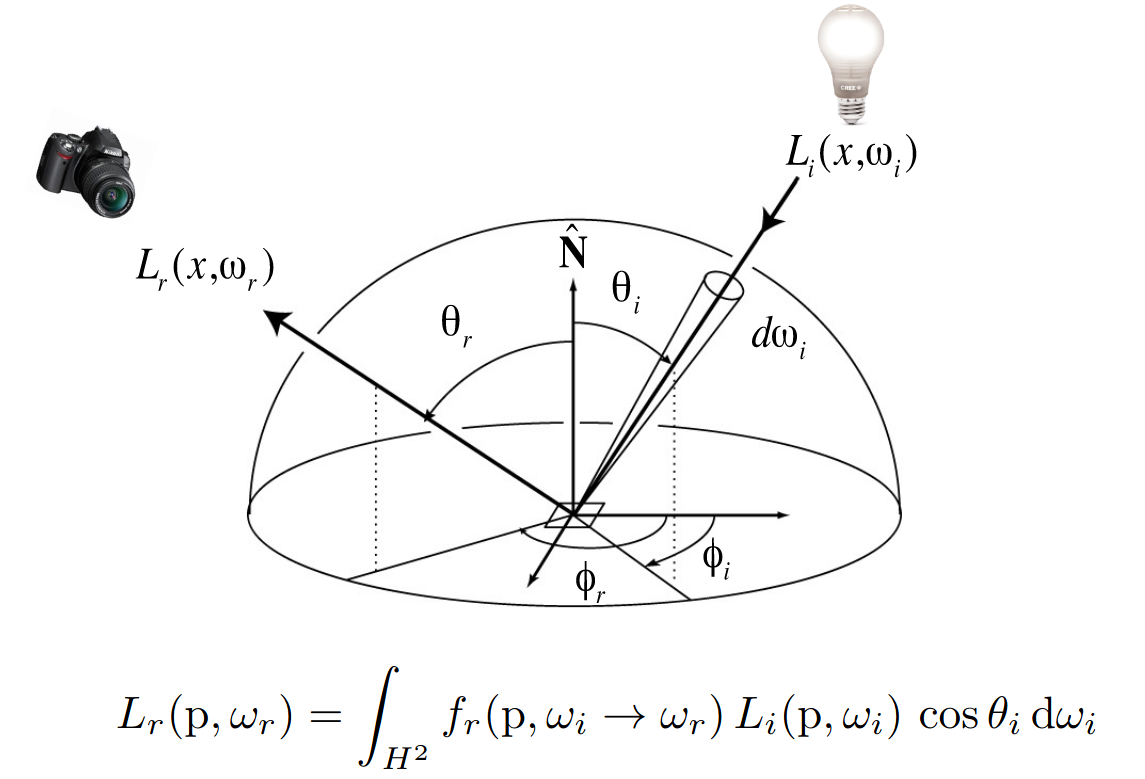
c593f1bf5bf64e66a0862674c806b20f.png

The Rendering Equation

加上着色点本身的辐射，即 Emission 项

Lo(p,ωo)=Le(p,ωo)+∫Ω+Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi)dωiL_{o}\left(p, \omega_{o}\right)=L_{e}\left(p, \omega_{o}\right)+\int_{\Omega^{+}} L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right) \mathrm{d} \omega_{i}

Ω+\Omega^{+} 代表半球面

we assume that all directions are pointing outwards

需要理解 Reflection 项积分符号的含义

当只有一个点光源时

Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi)L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right)

当有多个点光源时，求和即可

∑Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi)\sum L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right)

当光源有一定的大小，即非点光源时，积分即可

∫ΩLi(p,ωi)fr(p,ωi,ωo)(n⋅ωi)ωi\int_{\Omega} L_{i}\left(p, \omega_{i}\right) f_{r}\left(p, \omega_{i}, \omega_{o}\right)\left(n \cdot \omega_{i}\right) \omega_{i}

为了处理多次反射的情形，我们视反射光也为光源，将等式简化为

I(u)=e(u)+I(v)∫K(u,v)dvI(u) = e(u) + I(v) \int K (u, v) dv

考虑全局性，继续简化为

L=E+KLL = E + K L

L,EL, E are vectors, KK is the light transport matrix

可以解得

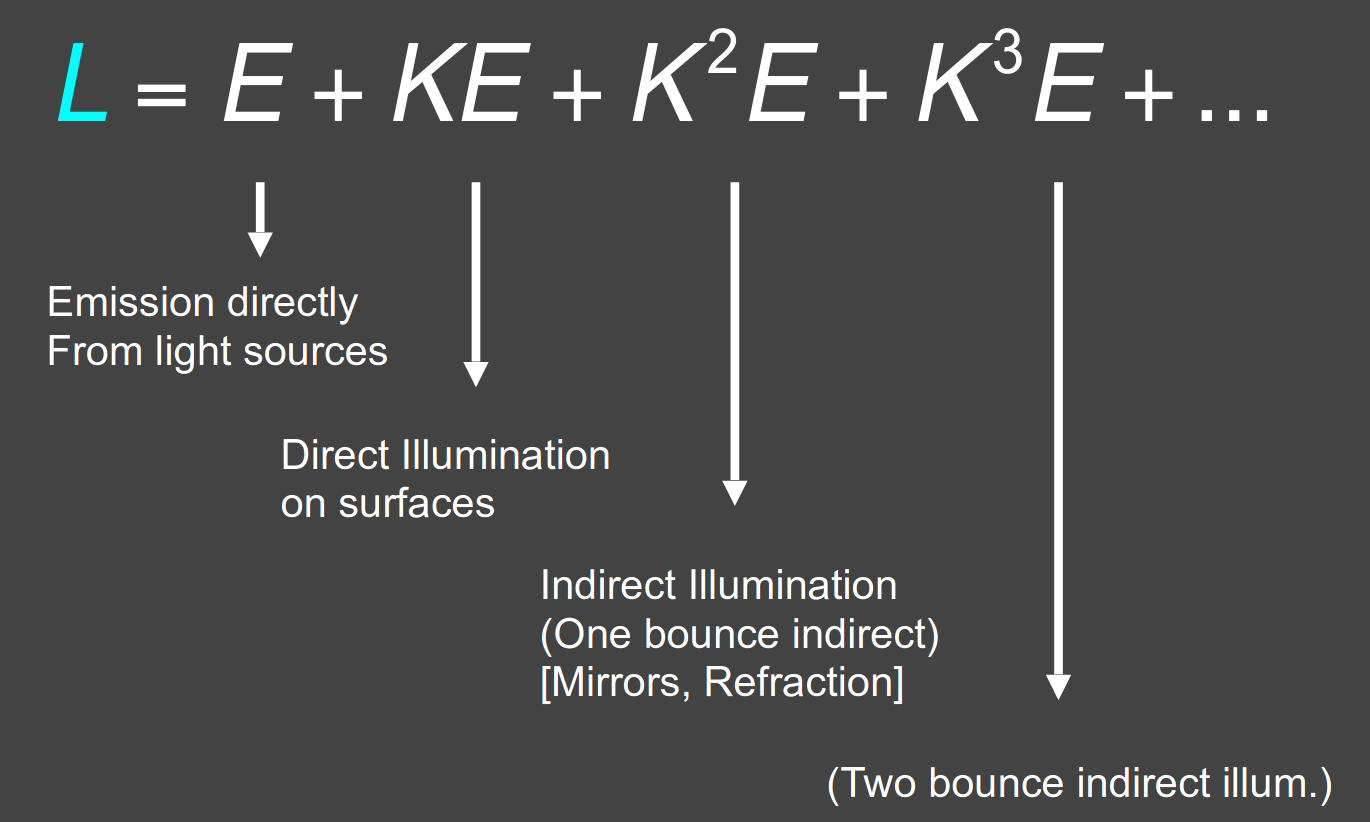
01d45977e3194717862a7f5271dc665a.png

注意之前所学的光栅化着色的 Shadow Mapping 只能计算前两项

除了第一项，其余部分即为 global illumination 全局光照

光线追踪（蒙特卡洛积分与路径追踪）

Monte Carlo Integration

数值方法求近似积分

∫abf(x)dx≈1N∑i=1Nf(Xi)p(Xi)Xi∼p(x)\int_a^b f(x) \mathrm{d} x \approx \frac{1}{N} \sum_{i=1}^{N} \frac{f\left(X_{i}\right)}{p\left(X_{i}\right)} \quad X_{i} \sim p(x)

XX 是连续型随机变量

以均匀分布为例，p(x)=1b−ap(x) = \frac{1}{b-a}，则

∫abf(x)dx≈b−aN∑i=1Nf(Xi)\int_a^b f(x) \mathrm{d} x \approx \frac{b-a}{N} \sum_{i=1}^{N} f\left(X_{i}\right)

Path Tracing

Whitted-Style Ray Tracing 有如下假设

然而这些假设并不合理

为此我们需要借助上节课的 The Rendering Equation 进行光线追踪

考虑计算全局光照，对于给定的着色点和观察方向

利用蒙特卡洛积分，有如下的算法

shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        Else If ray r hit an object at q
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo

注意这里的 wo,wiw_o, w_i

第一个分支计算直接光照，即第二项

第二个分支使用递归计算所有的间接光照，即第二项之后的项

注意对 wiw_i 取反方向

但需要注意这里递归会爆炸，有关系 rays = N ^ bounces

所以我们取 N = 1

shade(p, wo)
    Randomly choose ONE direction wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light
      Return L_i * f_r * cosine / pdf(wi)
    Else If ray r hit an object at q
      Return shade(q, -wi) * f_r * cosine / pdf(wi)

但随机性引入了噪声，所以我们需要在 ray_generation 时取 N 个方向

ray_generation(camPos, pixel)
    Uniformly choose N sample positions within the pixel
    pixel_radiance = 0.0
    For each sample in the pixel
        Shoot a ray r(camPos, cam_to_sample)
        If ray r hit the scene at p
          pixel_radiance += 1 / N * shade(p, sample_to_cam)
    Return pixel_radiance

SPP (samples per pixel)

然而上述着色算法仍存在问题，即递归可能不会终止

为此引入 Russian Roulette，即俄罗斯轮盘赌

这可以保证最终结果的期望相同

shade 算法如下

shade(p, wo)
    Manually specify a probability P_RR
    Randomly select ksi in a uniform dist. in [0, 1]
    If (ksi > P_RR) return 0.0;


    Randomly choose ONE direction wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light
      Return L_i * f_r * cosine / pdf(wi) / P_RR
    Else If ray r hit an object at q
      Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR

另外注意到，当光源较小时，shade 追踪的光线可能很难 hit 光源

为此考虑在光源平面，而非在着色点平面，进行采样

需要对 ff 进行变换

sample on x, integrate on x

6584842c98c44ac4ae946d210263f8a2.png

于是将着色分为两个部分

  1. light source (direct, no need to have RR)
  2. other reflectors (indirect, RR)

shade 算法最终如下

shade(p, wo)
    # Contribution from the light source.
    Uniformly sample the light at x’ (pdf_light = 1 / A)
  Shoot a ray from p to x’
  If the ray is not blocked in the middle
    L_dir = 0.0
  Else
    L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light


    # Contribution from other reflectors.
    L_indir = 0.0
    Test Russian Roulette with probability P_RR
    Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)
    Trace a ray r(p, wi)
    If ray r hit a non-emitting object at q
      L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR


    Return L_dir + L_indir

需要考虑到光源和着色点之间有 block 的情形

Further…

How? And in general, how to sample any function? (sampling)

What’s the best choice? (importance sampling)

Yes! (low discrepancy sequences)

Can I combine them? Yes! (multiple imp. sampling)

Why? (pixel reconstruction filter)

No. (gamma correction, curves, color space)

PA7

algorithm

伪代码如下

shade(p, wo)
  L_dir = 0.0
  sampleLight(inter, pdf_light)
  Get x, ws, NN, emit from inter
  Shoot a ray from p to x
  If the ray is not blocked in the middle
    L_dir = emit * eval(wo, ws, N) * dot(ws, N) * dot(ws, NN) / |x-p|^2 / pdf_light


  L_indir = 0.0
  Test Russian Roulette with probability RussianRoulette
  wi = sample(wo, N)
  Trace a ray r(p, wi)
  If ray r hit a non-emitting object at q
    L_indir = shade(q, wi) * eval(wo, wi, N) * dot(wi, N) / pdf(wo, wi, N) / RussianRoulette


  Return L_dir + L_indir

实现如下

// Implementation of Path Tracing
Vector3f Scene::castRay(const Ray &ray, int depth) const {
  // TODO: Implement Path Tracing Algorithm here
  Vector3f L_dir{};
  Vector3f L_indir{};


  Intersection inter_wo = this->intersect(ray);


  if (!inter_wo.happened) {
    return Vector3f{0};
  }


  // direct
  Vector3f wo = normalize(-ray.direction); // note negate
  Vector3f p = inter_wo.coords;
  Vector3f N = normalize(inter_wo.normal);


  Intersection inter_ws{};
  float pdf_ws{};
  this->sampleLight(inter_ws, pdf_ws);


  Vector3f x = inter_ws.coords;
  Vector3f NN = normalize(inter_ws.normal);
  Vector3f emit = inter_ws.emit;


  Vector3f ws = normalize(x - p);
  Ray ray_p_to_x(p, ws);


  Intersection inter_p_to_x = this->intersect(ray_p_to_x);
  // if (inter_p_to_x.happened && inter_p_to_x.obj->hasEmit()) { // assume
  if (inter_p_to_x.happened && (inter_p_to_x.coords - x).norm() < 0.01) {
    Vector3f eval_f_r = inter_wo.m->eval(ws, wo, N); // note order
    L_dir = emit * eval_f_r * dotProduct(ws, N) *
            dotProduct(-ws, NN) / // note negate
            ((x - p).norm() * (x - p).norm() * pdf_ws);
  } else {
    // the ray is blocked in the middle
    // do nothing
  }


  // indirect
  if (get_random_float() < this->RussianRoulette) {
    Vector3f wi = normalize(inter_wo.m->sample(wo, N));
    Ray ray_wi(p, wi);
    // Intersection intersection_wi = this->intersect(ray_wi);
    // if (intersection_wi.happened && !intersection_wi.obj->hasEmit()) {
    Vector3f shade = castRay(ray_wi, depth + 1);
    Vector3f eval_f_r = inter_wo.m->eval(wi, wo, N); // note order
    float pdf = inter_wo.m->pdf(wi, wo, N);
    L_indir =
        shade * eval_f_r * dotProduct(wi, N) / (pdf * this->RussianRoulette);
    // }
  } else {
    // do nothing
  }


  return L_dir + L_indir;
}

note

修改 Bounds3::IntersectP 中的相交条件

t_enter <= t_exit && t_exit >= 0

多一个等号

示意图如下

73a718fc1bfe443985726f198b079b33.svg

注意光线的方向，对 p 点而言，始终是 outwards

区分 eval 和 pdf 中的参数 wi 和 wo

关于检测光源和着色点之间是否有 block，需要射出额外的光线 ray_p_to_x，并判断交点和 x 点是否一致

关于间接光照，似乎并不需要分支判断

参数 depth 代表递归的次数，不过没有用到

thread

参考 https://github.com/Quanwei1992/GAMES101/blob/master/07/Renderer.cpp

使用多线程加速渲染，按 height 将屏幕划分给多个 worker

并且修改 CMakeLists.txt

find_package(Threads REQUIRED)
target_link_libraries(RayTracing PUBLIC Threads::Threads)

速度提升了约 2~3 倍

pic

128 spp

15b5494e63874ac0a1e47e0d04c99832.png

渲染了一个小时

todo

TODO

图形学对其他学科的要求挺高的……

而且调试完全没有头绪……

于是就这样吧……