TOC

Formal Semantics of Programming Languages

Info

https://hongjin-liang.github.io/teaching/semantics/index.html

Introduction

An overview of Coq

软件基础

A framework for certified software

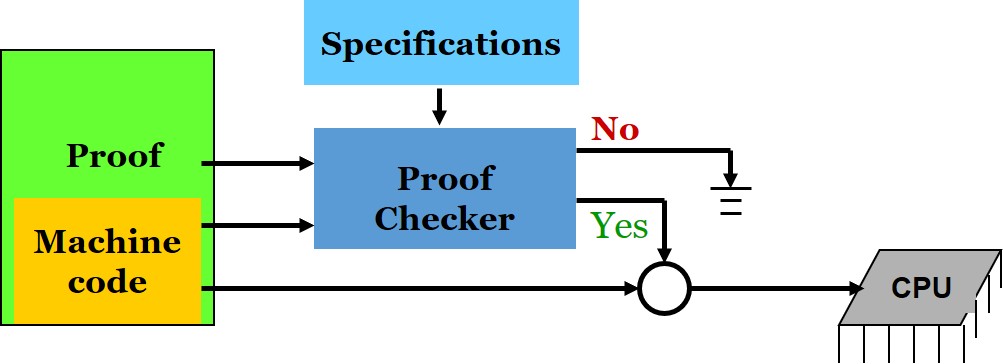
这里的 Proof Checker 便是 Coq

• logic
• proof assistants
• functional programming

lang.v

自然数和列表

• Module：模块

• Inductive：归纳

Inductive nat : Type :=
  | O : nat
  | S : nat -> nat.

Inductive even : nat -> Prop :=
| even_O: even O
| even_S: forall n, even n -> even (S (S n)).

Inductive natlist : Type :=
  | nil : natlist
  | cons : nat -> natlist -> natlist.

• Definition：函数

Definition pred (n : nat) : nat :=
  match n with
    | O => O
    | S n' => n'
  end.

• Fixpoint：递归函数

Fixpoint mult (n m : nat) : nat :=
  match n with
    | O => O
    | S n' => plus m (mult n' m)
  end.

• Proof. ... Qed.：证明

Lemma plus_S:
  forall m n, plus m (S n) = S (plus m n).
Proof.
  induction m.
  - auto.
  - intro n. simpl.
    rewrite -> IHm.
    reflexivity.
Qed.

• Notation：记号

Notation "x :: l" := (cons x l) (at level 60, right associativity).
Notation "[ ]" := nil.
Notation "[ x ; .. ; y ]" := (cons x .. (cons y nil) ..).

• Check：类型检查
• Print：具体信息
• Compute：计算

逻辑

使用 mermaid 画出类型之间的关系

在 Coq 里试试：

Print and.
Check and.
Locate "/\".
Check conj.

Print iff.
Check iff.
Locate "<->".

Print or.
Check or.
Locate "/\".
Check or_introl.
Check or_intror.

Print False.
Print True.

Print not.
Check not.
Locate "~".

Locate "<>".

Print eq.
Check eq.

Maps.v

TODO

Imp.v

TODO

Mathematical Background

• Generalized Products
• Generalized Sums

Lambda Calculus

Syntax

(Terms) M, N ::= x | λx. M | M N

Conventions

• Body of λ extends as far to the right as possible
• Function applications are left-associative

Free and bound variables

The set of free variables of a term $M$ is denoted $FV(M)$​.

α-equivalence

rename

β-reduction

(capture-avoiding) substitution

reduction rules

非确定性

Normal form

• β-redex: a term of the form (λx.M) N
• β-normal form: a term containing no β-redex

Confluence (Church-Rosser Property)

形式化：→*

推论：With α-equivalence, every term has at most one normal form.

Reduction strategies

• Normal-order reduction: choose the left-most, outer-most redex first
• Applicative-order reduction: choose the left-most, inner-most redex first

确定性引入

Evaluation

不化简函数体

• Only evaluate closed terms (i.e. no free variables)
• May not reduce all the way to a normal form
• Terminate as soon as a canonical form (i.e. a lambda abstraction) is obtained

• A closed normal form must be a canonical form
• Not every closed canonical form is a normal form

• Normal-order evaluation rules
• Eager evaluation rules

⇒ / →

Programming in λ-calculus

• Booleans
• Natural numbers
• Pairs
• Lists
• Trees
• Recursive functions

Y = lambda f: (lambda x: x(x))(lambda x: f(lambda z: x(x)(z)))
fib_maker = lambda f: lambda r: 1 if (r == 0) else r * f(r - 1)
number_of_six_maker = lambda f: lambda r: (1 if r[0] == "6" else 0) if len(r) == 1 else (1 if r[0] == "6" else 0) + f(r[1:])

my_fib = Y(fib_maker)
my_number_of_six = Y(number_of_six_maker)

print(my_fib(3))
print(my_number_of_six("666666"))

https://nju-sicp.bitbucket.io/2021/hw/hw03/3_2.html

Simply-Typed Lambda Calculus

Graduate Programming Languages (washington.edu)

Syntax

(Types) τ, σ ::= T | σ -> τ
(Terms) M, N ::= x | λx:τ.M | M N

Typing judgment

Γ ⊢ M:τ

M is of type τ in context Γ

Typing rules

• var
• app
• abs

Soundness and completeness

• Type system cannot be sound and complete.
• Choose soundness, try to reduce false positives in practice.

Type Safety

• Preservation
• Progress

Strong normalization theorem

Well-typed terms in STLC always terminate.

Adding stuff

• Extend the syntax (types & terms)

• Extend the operational semantics (reduction rules)

• Extend the type system (typing rules)

• Extend the soundness proof (new proof cases)

• Product type

• Sum type

• Recursion: strong normalization is eliminated.

Curry-Howard isomorphism

(Prop)  p, q ::= B | p ⇒ q | p ∧ q | p ∨ q
(Types) τ, σ ::= T | σ -> τ | σ × τ | σ + τ

• Propositions are Types

• Proofs are Programs

• can be proved in propositional logic ⇔ have closed terms

• cannot be proved in propositional logic ⇔ no closed terms

• Constructive propositional logic ⇔ STLC with Product and Sum type

• Classical propositional logic has the law of the excluded middle

• STLC with Recursion is inconsistent

But every logic has a corresponding typed system.

Operational Semantics

Syntax of a Simple Imperative Language

• 整数表达式：$e$
• 布尔表达式：$b$
• 命令（语句）：$c$

注意区分语法中的 numerals 和语义中的 natural numbers

• We write $\lfloor x \rfloor$ to denote the meaning of $x$.
• We assume that $\lfloor n \rfloor = n$​.​

Small-step operational semantics

Structural

• syntax oriented
• inductive

State

(State) σ $\in$ Var $\to$ Values

数学基础：单点修改

$\leadsto$

Operational semantics will be defined using configurations of the forms $(e, σ)$.

IntExp

Define $\longrightarrow$ as relation between the pair of IntExp and State

(IntExp) e ::= n | x | e + e | e - e | ...

求值顺序

BoolExp

We overload the symbol $\longrightarrow$.

(BoolExp) b ::= true | false | e = e | e < e | e > e | ¬b | b ^ b | b ∨ b | ...

短路求值

Comm

(Comm) c ::= skip | x := e | c ; c | if b then c else c | while b do c

skip

(skip, σ) -> σ

assignment

(e, σ) -> (e', σ) => (x := e, σ) -> (x := e', σ)
(x := n, σ) -> σ{x ~> [n]}

注意上下两行的箭头类型并不相同

while

(while b do c, σ) -> (if b then (c ; while b do c) else skip; σ)

Zero-or-multiple steps

定义 $\longrightarrow$ ​​的自反传递闭包即可

Some facts about $\longrightarrow$

• Determinism

• Confluence

• Normalization

Every evaluation path eventually reaches a normal form.

Normal forms:

For expressions, the normal forms are (n, σ) for numeral n.

For booleans, the normal forms are (true, σ) and (false, σ).

The transition relations on (e, σ) and (b, σ) are normalizing.

The transition relation on (c, σ) is not normalizing.

(while true do skip, σ) ->* σ'

Variation

1. 由之前的 Normalization 的性质，我们可以对嵌在语句中的表达式进行单独求值，在语句层面上只有一步。进而优化 Comm 中 $\longrightarrow$ ​​的定义
2. 统一箭头类型，如 (x := n, σ) -> (skip, σ{x ~> [n]})

Here skip is overloaded as a flag for termination.

So there is no rule for (skip, σ), do not forget to modify the rules of sequential composition.

优化后完整的 Comm 的 $\longrightarrow$​​ 的定义见讲义

下面的拓展建立在这样的基础上

Going wrong

Take Divide by 0 for exemple.

abort

We distinguish “going wrong” from “getting stuck”.

• In the semantics “Version II”, skip gets stuck at any state.
• Note both notions are language-dependent.

Local variable declaration

c ::= ... | newvar x := e in c

前提：

• 对 e 求值得 n
• (c, σ{x ~> n}) -> (c', σ')
• n' = σ' x

state 可能变化，所以应重新对 n 进行 lookup

转移：

• (newvar x := e in c, σ) -> (newvar x := n' in c', σ'{x ~> σ x})

应保持全局的 x 不变，考虑并发

A simple language with heap manipulation

可以视为引入内存

首先修改 state，增加堆区：

(States) σ ::= (s, h)
(Stores) s ∈ Var -> Values
(Heaps)  h ∈ Loc -> Values (remark: partial mapping)
(Values) v ∈ Int ∪ Bool ∪ Loc

在**语句（指令）**层面增加语法：

c ::= ... | x := alloc(e) | free(x) | y := [x] | [x] := e

从而表达式部分的语义保持不变

区分 [x] 为左值（地址）还是右值（值）

Contextual semantics

Another form of small-step operational semantics

对原始版本而言，而非变体

引入目的：合并相同结构的转换规则 (Global reduction rule)

redex

A redex is a syntactic expression or command that can be reduced (transformed) in one atomic step.

没有子结构的转移条件

For brevity, below we mix expression and command redexes:

(Redex) r ::= x | n + n | x := n | skip ; c | if true then c else c | if false then c else c | while b do c ...

Local reduction rules

evaluation context

An evaluation context is a term with a “hole” in the place of a sub-term.

For example, x := 1 + [] is an evaluation context ε. Filling hole with 2 + 8 yields ε[2 + 8] = (x := 1 + (2 + 8)).

Filling hole with redex.

Location of the hole indicates the next place for evaluation.

(Ctxt) ε ::= [] | ε + e | n + ε | x := ε | ε ; c | if ε then c else c | ...

while -> if, so while $\notin$ Ctxt

decomposition

递归进行分解：

• exist
• unique (based on Determinism)

example

x := 1 ; x := x + 1 in the initial state {x ~> 0}

for boolean expressions

非短路和短路