TOC
Open TOC
info
new
su21
textbook
Introduction to Cryptography
Alice, Bob, Eve, and Mallory
密码学中角色阵容中反复出现的两个成员是 Alice 和 Bob,他们希望安全地进行通信
但是,他们只有一条电话线或互联网连接,可以由窃听对手 Eve 窃听
adversaries
在某些场景中,Eve 可能会被活跃的对手 Mallory 取代,除了窃听他们之外,他还可以篡改通信
目标是设计一个方案来扰乱 Alice 和 Bob 之间的消息,使 Eve 对他们交换的内容一无所知,并且 Mallory 无法在不被发现的情况下篡改他们交换的内容
换句话说,我们希望仅使用可用的不安全通道来模拟理想的通信通道
key
任何加密系统的最基本构建块都是密钥
现代密码学中有两种主要的密钥模型
- 在对称密钥模型中,Alice 和 Bob 都知道密钥的值,并且必须使用此共享密钥值来保护其通信
- 在非对称密钥模型中,每个人都有一个密钥和一个相应的公钥
Confidentiality, Integrity, Authenticity
Confidentiality 是防止对手读取我们的私人数据的属性。如果消息是机密消息,则攻击者不知道其内容
Integrity 是防止对手篡改我们的私人数据的属性。如果消息具有完整性,则攻击者无法在未被检测到的情况下更改其内容
Authenticity 是允许我们确定谁创建了给定消息的属性。如果一条消息具有真实性,那么我们可以确定该消息是由声称撰写它的人写的
两种密钥模型对应的方案如下
| Symmetric-key | Asymmetric-key | |
|---|---|---|
| Confidentiality | Block ciphers with chaining modes (e.g., AES-CBC) | Public-key encryption(e.g., El Gamal, RSA encryption) |
| Integrity and authentication | MACs (e.g., AES-CBC-MAC) | Digital signatures (e.g., RSA signatures) |
其余一些 cryptographic primitives 加密原语
- Cryptographic hashes
如 SHA-256
- pseudo random number generator
伪随机数生成
- Key exchange schemes (e.g. Diffie-Hellman key exchange)
允许 Alice 和 Bob 使用不安全的通信通道就共享的随机密钥达成一致,该密钥随后用于对称密钥加密
Kerckhoff’s Principle
我们将假设攻击者知道加密和解密算法
攻击者唯一缺少的信息是密钥
Threat models
- ciphertext-only attack
Eve 未掌握了明文的任何信息,希望通过密文恢复明文
- known plaintext attack
Eve 已经掌握了一些关于明文的部分信息,希望通过密文恢复明文
- replay attack
Eve 可以捕获从 Alice 到 Bob 的加密消息,然后再次将加密消息重新发送给 Bob
- chosen-plaintext attack
Eve 可以欺骗 Alice 加密 Eve 选择的任意消息,然后 Eve 可以观察得到的密文
本课程将主要关注针对选择明文攻击的安全性
- chosen-ciphertext attack
Eve 可以欺骗 Bob 解密一些给定的密文
- chosen-plaintext/ciphertext attack
chosen-plaintext attack + chosen-ciphertext attack
Symmetric-Key Encryption
IND-CPA Security
我们需要尽可能形式化 Confidentiality
考虑在 chosen-plaintext attack 这个 Threat models 下
我们进行 IND-CPA game
- Eve 选择两个不同的消息 发送给 Alice
- Alice 等概率加密某条消息,并发送给 Eve
- Eve 执行 chosen-plaintext attack
- 若 Eve 能够猜测步骤 2 中的加密消息是 还是 ,则加密方案不是 IND-CPA Security,否则是 IND-CPA Security
简单来说,攻击者不能从密文中得到关于明文的额外信息
联系信息论
有几个要点
- 消息 的长度必须相同
引理:我们允许密文泄漏明文的长度
否则对于任意长度的明文,都需要使用相同长度的密文来加密,这并不实际
而且,如果密文始终为 位长,那么我们将无法加密任何超过 位的明文
由于密文能够泄漏明文的长度,所以 Eve 可以通过密文的长度来辨别消息 ,那么上述游戏就会就会错误地将某些 IND-CPA 安全方案标记为不安全的
- chosen-plaintext attack 的数量有实际的限制
在暴力破解下没有绝对的安全
Eve 在游戏期间使用的任何算法都必须是多项式级别的复杂度
- 只有当 Eve 拥有不可忽视的优势时,她才会获胜
同样是考虑实际,概率太小没有意义
- 注意到任何 IND-CPA 安全方案都是非确定性的
否则在 chosen-plaintext attack 中继续发送消息 就可以轻松辨别
One Time Pad
使用异或操作的一个简单加密方案
- Key generation: Alice and Bob pick a shared random key
- Encryption algorithm:
- Decryption algorithm:
只要 是均匀生成的,该方案便是 IND-CPA 安全方案,证明如下
其中 是消息的下标, 为消息的长度
注意不能使用相同的 加密不同的明文
如果 重用以加密两条消息 和
Eve 可以取两个密文的异或
得到
这提供了有关这两条消息的额外信息
另一个角度看,算法中引入了确定性
Block Ciphers
在大多数对称加密方案中,Alice 和 Bob 共享一个密钥,并使用此单个密钥重复加密和解密消息。
分组密码是实现这种对称加密方案的基本构建块。
The block cipher has different settings for scrambling, so it also takes in a -bit key as input to determine which scrambling setting should be used.
加密函数如下
固定 后,有
解密函数满足
上面定义的分组密码是一类函数,这意味着分组密码有许多不同的实现
如今,最常用的分组密码实现称为高级加密标准 AES
分组密码本身不是 IND-CPA 安全的,因为它们是确定性的
但是,分组密码在计算上与随机排列无法区分
这将有助于我们构建 IND-CPA 安全对称加密方案
为了消除确定性,加密算法可以是随机的,也可以是有状态的
但是,解密算法既不是随机的,也不是有状态的
使用分组密码构建加密算法有几种标准方法
以 CBC Mode (Cipher Block Chaining) 为例
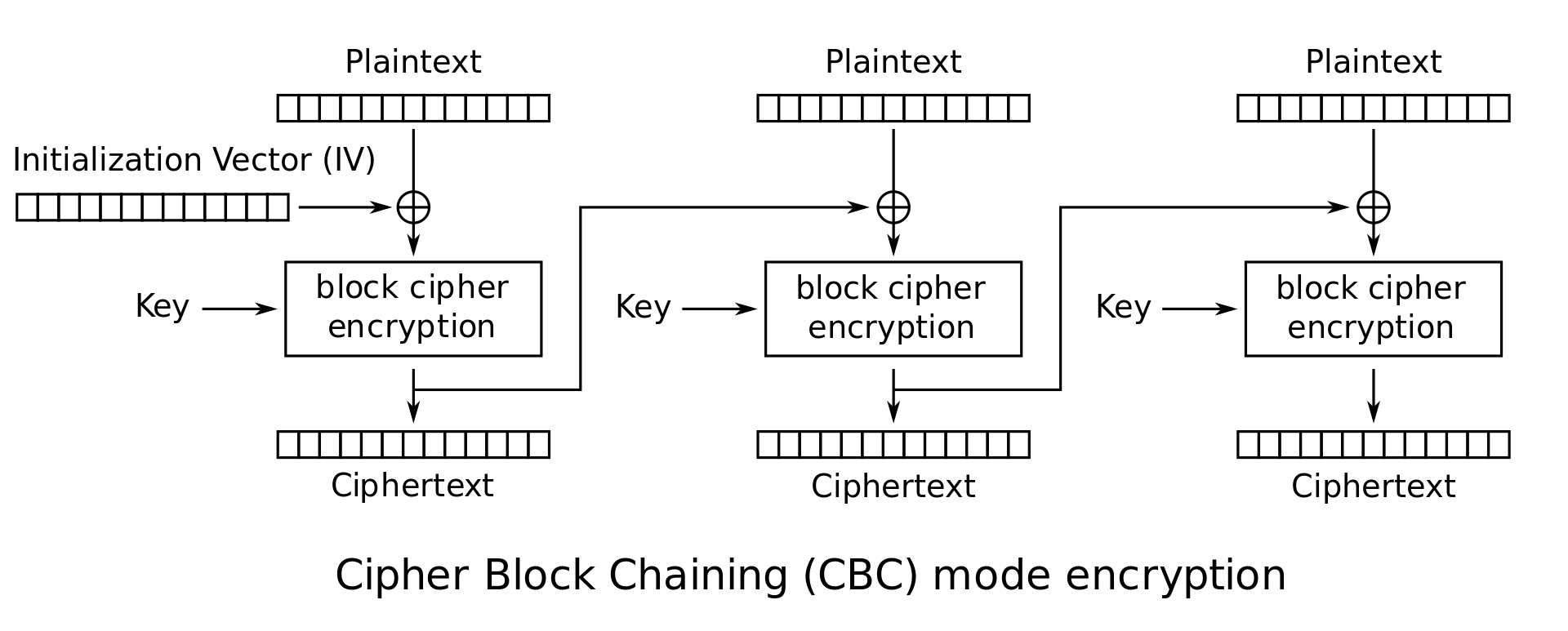
For each message the sender picks a random -bit string, called the initial vector or IV.
加密如下
解密如下
显然,该 CBC Mode 加密无法并行化,但是其他一些 mode 可以并行化
CBC Mode 使用随机的 IV 消除确定性
另外,分组密码允许我们加密长度超过一个区块的消息
如果我们想发送的消息不是块大小的倍数,需要进行填充
Cryptographic Hashes
哈希函数 是确定性的
通常,加密哈希函数的输出是固定大小的
加密哈希函数有几个有用的属性
- One-way / preimage resistant
给定 计算 很容易
给定 求解 不可行 infeasible
- Second preimage resistant
给定 ,寻找 使得 不可行
- Second preimage resistant
寻找 使得 不可行
By infeasible, we mean that there is no known way to accomplish it with any realistic amount of computing power.
今天,有两个主要的哈希算法家族被认为是安全的,即 SHA2 和 SHA3
在每个系列中,都有不同的输出长度
SHA-256、SHA-384 和 SHA-512 都是 SHA2 系列的实例,输出分别为 256b、384b 和 512b
而 SHA3-256、SHA3-384 和 SHA3-512 是 SHA3 系列成员
通过将哈希函数的输出长度与对称加密算法的密钥长度相关联,我们可以确保攻击者同样难以破坏任何一种方案
例如,如果我们使用的是 AES-128,我们应该使用 SHA-256 或 SHA3-256
加密哈希在加密之外还有许多实际应用,比如利用输出的随机性,通过统计方法进行一些验证
详见 https://textbook.cs161.org/crypto/hashes.html#74-lowest-hash-scheme
Message Authentication Codes (MACs)
在构建保证完整性和身份验证的加密方案时,我们担心的威胁是发送伪装来自合法参与者的消息(欺骗)或修改合法参与者发送的消息内容(篡改)的对手
为了应对这些威胁,我们将引入加密方案,使收件人能够检测欺骗和篡改,这便是 MAC
由于 MAC 是对称密钥加密原语,因此在本节中,我们可以假设 Alice 和 Bob 共享一个其他人都不知道的密钥
MAC 接受固定长度的密钥和任意长度的消息,并输出固定长度的校验和
MAC 必须具有确定性才能获得正确性,因为 Bob 需要使用 MAC 计算校验和
安全的 MAC 算法有如下属性
- 攻击者无法为从未见过的消息创建有效的 MAC,即在 chosen-plaintext attack 威胁模型下是安全的
下面考虑构造安全 MAC 的方案,我们介绍一种称为 AES-EMAC 的算法
计算如图所示
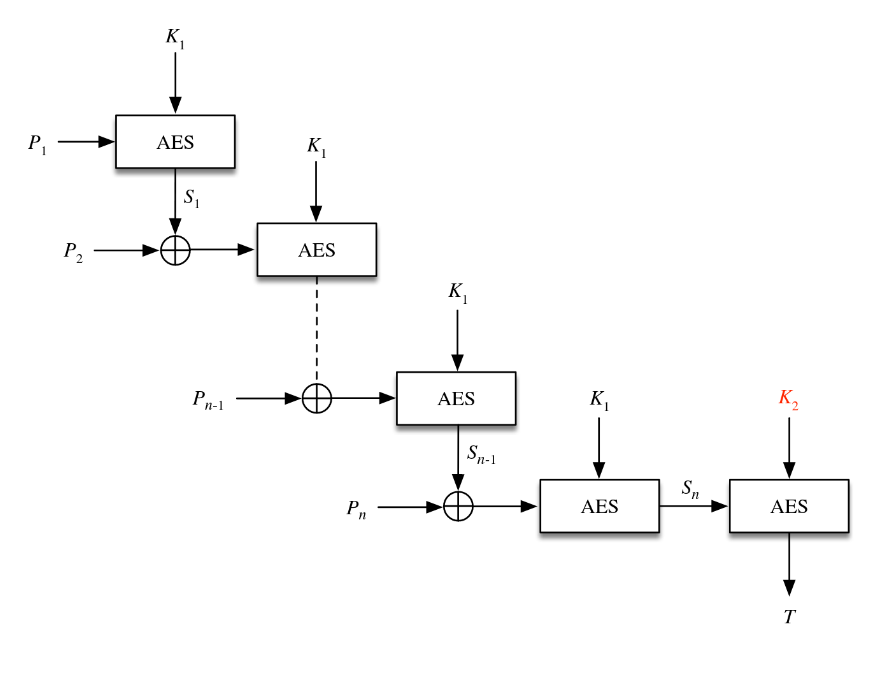
将明文划分为块,使用两个不同的密钥
对于下标形式,请回顾 Block Ciphers
另外,也可以使用加密哈希函数的加密属性来构造安全的 MAC 算法
HMAC 是一个出色的结构,因为它结合了 MAC 和底层哈希的优点
- 如果没有密钥,标记不会泄漏有关消息的信息
- 即使使用密钥,从哈希输出重建消息在计算上也是棘手的
其计算如下
注意 通过填充或者哈希的方式变成 位
HMAC 算法使用两个硬编码的 opad 和 ipad 从单个密钥生成两个不相关的密钥
别忘了 为连接操作
需要注意的是,MAC 并不能保证 confidential
所以需要一种方案,同时保证消息的 Confidentiality, Integrity, Authenticity
以 authenticated encryption 为例
Suppose we have an IND-CPA secure encryption scheme Enc that guarantees confidentiality, and an unforgeable MAC scheme MAC that guarantees integrity and authenticity.
There are two main approaches to authenticated encryption
- encrypt-then-MAC
发送二元组
- MAC-then-encrypt
发送一个值
在这两种方法中,Enc 和 MAC 应使用不同的密钥
There are also some special block cipher operation modes, known as AEAD (Authenticated Encryption with Additional Data).
The additional data component means that the integrity is provided not just over the encrypted portions of the message but some additional unencrypted data.
Pseudorandom Number Generators
正如我们在前面的章节中看到的那样,密码学通常需要随机性
在密码学中,我们通常希望随机性具有最多的熵
一个好的伪随机数算法生成的位在计算上与真随机生成的位无法区分
伪随机数生成器 pRNG 是一种算法,它采用少量真正的随机位作为输入,并输出一长串伪随机位
初始的真正随机输入称为种子
pRNG 算法是确定性的,所以,我们并不想每一次生成随机数都提供一个新的种子
理想情况下,我们希望 pRNG 接收初始种子,然后根据需要生成任意数量的伪随机位
为此,pRNG 需要维护一些内部状态,并在 pRNG 生成新随机数或接收种子作为输入时更新状态
正式地说,pRNG 由以下三个函数定义
Seed(entropy)
接收一些初始的真正随机熵并初始化 pRNG 的内部状态
Reseed(entropy)
吸收一些额外的真正随机熵,根据需要更新 pRNG 的内部状态
Generate(n)
生成 位伪随机数,根据需要更新内部状态
某些 pRNG 还支持在此步骤中直接添加额外的熵
对于安全的 pRNG 而言,如果攻击者不知道种子和内部状态,则其输出在计算上与随机无法区分
我们还希望安全的 pRNG 具有 rollback resistance,即使攻击者在某一时刻获取了 pRNG 的内部状态,攻击者也无法推断出有关任何先前生成的随机数的任何内容
pRNG 有许多实现,但实践中常用的 pRNG 之一是 HMAC-DRBG,它使用 HMAC 的安全属性来构建 pRNG
HMAC-DRBG 的内部状态为
对应的函数如下
- generate

- seed

在 seed 算法中使用加密哈希函数意味着 HMAC-DRBG 可以接受任意长的初始种子
注意到加密哈希函数的 preimage resistant 性质,HMAC-DRBG 也具有 rollback resistance
另外,pRNG 配合 one-time pad 也是一种加密方案,被称为 Stream ciphers
Diffie-Hellman key exchange
在之前的讨论中,我们假设 Alice 和 Bob 都共享一个其他人不知道的密钥
但是,如果他们只能通过不安全的渠道进行通信,他们如何能够交换密钥呢
Diffie-Hellman 方案实际上是双方在面对窃听者时就随机值达成一致的一种方式
启发 -> 混合两种颜色很容易,但分离两种颜色的混合物几乎是不可能的
其数学对应就是 one-way functions
给定 求解 不可行
一些 one-way functions 的例子
- exponentiation modulo a prime (discrete log modulo)
where is a large prime and is a specially-chosen generator
- elliptic-curve
我们以 exponentiation modulo a prime 为例
参数 是公开的标准
Alice 随机选取 ,发送
Bob 随机选取 ,发送
Alice 接收到 后,计算
Bob 接收到 后,计算
于是得到共享密钥
然而 Eve 仅通过 计算 是不可行的
下面是破解的难度比较
In practice, it is generally believed that computing the discrete log modulo a 2048b prime, computing the elliptic curve discrete log on a 256b curve, and brute forcing a 128b symmetric key algorithm are all roughly the same difficulty.
需要注意,如果允许攻击者篡改消息,比如对手 Mallory,那么 Diffie-Hellman 方案就可能会崩溃
具体如图所示
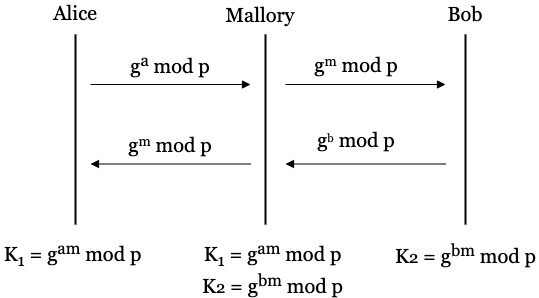
所以加密方案需要同时具有 Confidentiality, integrity and authenticity
Public-Key (Asymmetric) Encryption
在某些情形下,对称密钥加密可能不方便使用,因为它需要 Alice 和 Bob 以某种方式进行协调并建立共享密钥
非对称加密,也称为公钥加密,旨在解决此问题
在公钥密码系统中,接收者 Bob 有一个公开可用的密钥,即他的公钥,每个人都可以访问
当 Alice 希望向他发送消息时,她使用他的公钥来加密她的消息
Bob 还有一个密钥,他的私钥,可以让他解密这些消息
trapdoor one-way function
公钥加密的数学基础是 one-way functions 的一个变体 trapdoor one-way function
也就是为求解 开了后门
这个后门便是 Bob 的私钥
一些 trapdoor functions 的例子
- RSA Hardness
STFW
- Discrete log problem
已知 ,只要知道了 或 ,就可以计算出
El Gamal encryption
注意到 Diffie-Hellman 方案只能让双方就随机值达成一致
一种基于此方案的 El Gamal 加密允许 Alice 和 Bob 交换加密消息
假定系统参数 ,Bob 有私钥 ,公钥
Alice 有消息 ,Alice 随机选择 ,并发送
然后 Bob 就可以解密得到明文
类似 Diffie-Hellman 方案,这里对应的达成一致的随机值为
Alice 通过发送 加密明文
注意到 的随机性,联系 one-time pad 的 Confidentiality,可以认为这种加密算法是 Confidentiality 的
另一个分析的角度是 discrete log problem
攻击者已知 ,但计算 是不可行的
然而 Bob 有后门 ,所以计算 是可行的
Public Key Distribution
一切看起来都很棒,但问题是,如果 Alice 和 Bob 想要使用这些公钥方法安全地进行通信,他们需要某种方法来安全地学习彼此的公钥
这里介绍的算法并不能帮助 Alice 公钥是否是 Bob 的
也就是说,攻击者可以假装是 Bob 广播自己的公钥
即算法不具备 Authenticity
Session Keys
需要注意,公钥方案成本高昂且难以满足 IND-CPA 安全的要求
因此我们倾向于仅使用公钥加密来分发一个或多个会话密钥
会话密钥是用于实际加密和验证消息的密钥
Digital Signatures
在本节中,我们将定义数字签名,这些数字签名本质上是 MAC 的公钥版本,并展示它们如何帮助保证 integrity 和 authenticity
在数字签名方案中,Bob 生成公钥(也称为验证密钥)和私钥(也称为签名密钥)
Bob 将其验证密钥分发给所有人,但对签名密钥保密
当 Bob 想要发送消息时,他使用其签名密钥在消息上生成签名
当 Alice 收到邮件时,她可以使用 Bob 的验证密钥来检查签名是否有效
抽象成三个算法
- Key generation
- Signing
- Verification
High-level Outline
先做如下记号
- a trapdoor one-way function
- a one-way function
- verification key
- signing key
则
如果有 signing key ,则给定 ,可以这样计算
相当于 给计算 开了后门
Number Theory Background
直接截图了

RSA Signatures
下面描述 RSA 签名方案
使用 Theorem 1 中的 作为 a trapdoor one-way function
因为很容易发现 为计算 开了后门呢
于是有
Certificates
鉴于密码学的成功,可以说其有效使用的最大挑战恰恰与这些密钥以及如何管理它们有关
假设 Alice 想通过不安全的通信通道与 Bob 安全地通信,但她不知道他的公钥
一个天真的策略是,她可以给 Bob 发一条消息,要求他发送他的公钥
然而,Mallory 可以篡改 Bob 的响应,将 Bob 响应中的公钥替换为 Mallory 的公钥
并且,在解密 Alice 发送的密文并得知 Alice 想要发送的秘密消息后,Mallory 可以用 Bob 的公钥重新加密 Alice 的消息
Mallory 可以在两个方向上发起类似的攻击,于是 Alice 和 Bob 向对方发送的所有秘密信息都会被泄露,但 Alice 和 Bob 却一无所知
这被称为中间人攻击 man-in-the-middle (MITM)
防止 MITM 攻击的一般策略是确保每个参与者都可以验证其他人公钥的真实性,有如下几种方案
Trusted Directory Service
使用受信任的目录服务,某些组织维护每个参与者的名称与其公钥之间的关联
另外,Alice 需要知道目录服务的公钥,一种方案是在依赖于目录服务的所有应用程序的源代码中硬编码目录服务的公钥
但是,这种方案有许多限制,具体见 https://textbook.cs161.org/crypto/certificates.html#132-trusted-directory-service
Digital Certificates
这种方案的基础是上一节中的数字签名
一个受信任的人拥有
- verification key
- signing key
他为 Bob 签署了一份公钥的声明,即数字证书
如果 Alice 想要安全地与 Bob 通信,她可以获得此证书的副本,然后使用 进行解密
在实际应用中,通常是由 Certificate Authority (CA) 来颁发证书
这种方案还可以用于保护 Web 安全
希望通过 SSL (https:) 提供访问权限的网站可以从 CA 购买数字证书,CA 检查网站的身份并颁发将网站的域名链接到其公钥的证书
世界上每个浏览器都附带一个受信任的 CA 列表。当您在 Web 浏览器中键入 URL 时,它将连接到网站,要求提供站点数字证书的副本,使用颁发证书的 CA 的公钥验证证书,检查证书中的域名是否与您要求访问的站点匹配,然后使用数字证书中的公钥与该站点建立安全通信
另外,这种证书的颁发还可以形成层次结构,即证书链
每个证书都对链中下一个证书签名的一方的公钥进行身份验证
对于证书的撤销,有如下两种方案
- Validity periods
- Revocation lists
Web of Trust
Another approach is the so-called web of trust, which was pioneered by PGP, a software package for email encryption. The idea is to democratize the process of public key verification so that it does not rely upon any single central trusted authority. In this approach, each person can issue certificates for their friends, colleagues, and others whom they know.
Leap-of-Faith Authentication
首次使用时的信任
如 SSH 连接
Passwords
从安全角度来看,我们可以识别与密码身份验证相关的许多安全风险
- Eavesdropping
- Client-side malware
- Online guessing attacks
- Server compromise
- …
我们将在下面介绍每种风险的防御和缓解措施
Mitigations for eavesdropping
使用 SSL (https:) 连接
这将确保用户名和密码通过加密通道发送,因此窃听者无法了解用户的密码
Mitigations for client-side malware
防范客户端恶意软件非常困难
主要的防御措施是双因素身份验证,我们将密码与其他形式的身份验证相结合
Mitigations for online guessing attacks
首先需要了解密码的分布
- 大约 1% 的用户从前 10 个最常用的密码中选择密码
- 尝试 个最常用的密码,就可以期望猜出大约 50% 的用户密码
需要区分针对性攻击和非针对性攻击
下面是一些措施
- 对可以做出的连续错误猜测的数量施加限制
- 验证码
- 密码强度
Mitigations for server compromise
当服务器被入侵后,其数据库中的内容将会泄漏
所以以明文形式存储密码不是一个好主意
一种简单的方法是使用加密哈希函数对每个密码进行哈希处理,并将哈希值存储在数据库中
不幸的是,这个简单的想法有一些缺陷
- Offline password guessing
考虑非针对性攻击,对每个用户,攻击者对 个最常用的密码进行哈希处理,然后进行比对
由于计算加密哈希函数非常快。这让攻击者可以快速测试许多猜测
- Amortized guessing attacks
甚至不需要对每个用户分别处理,攻击者对 个最常用的密码进行哈希处理,然后二分查找每个用户对应的哈希值
为此,需要有一种更好的方法来存储服务器上的密码
例如,为每个用户选定一个随机值 ,对于密码 ,存储哈希值
这样可以规避 Amortized guessing attacks
另一方面,我们需要使用 slow hash,例如对于加密哈希函数 ,我们使用
综合两方面,对每个用户,在数据库中存储二元组
go
command
go help
RTFM
go run xxx.go
直接编译运行
go build
在项目目录下生成可执行文件
go install
将编译后的包文件放到 pkg 目录下
将可执行文件放到 bin 目录下
debug
$ go install github.com/go-delve/delve/cmd/dlv@master可执行文件在 GOBIN 中
$ dlv debug a.gomodule
https://juejin.cn/post/6844903808942735368
$ go mod init main$ go get golang.org/x/tour/picdeclaration
https://blog.go-zh.org/gos-declaration-syntax
control flow
https://blog.go-zh.org/defer-panic-and-recover
defer
在函数返回后保证解锁
package main
import ( "fmt" "sync" "time")
// SafeCounter 的并发使用是安全的。type SafeCounter struct { v map[string]int mux sync.Mutex}
// Inc 增加给定 key 的计数器的值。func (c *SafeCounter) Inc(key string) { c.mux.Lock() // Lock 之后同一时刻只有一个 goroutine 能访问 c.v c.v[key]++ c.mux.Unlock()}
// Value 返回给定 key 的计数器的当前值。func (c *SafeCounter) Value(key string) int { c.mux.Lock() // Lock 之后同一时刻只有一个 goroutine 能访问 c.v defer c.mux.Unlock() return c.v[key]}
func main() { c := SafeCounter{v: make(map[string]int)} for i := 0; i < 1000; i++ { go c.Inc("somekey") }
time.Sleep(time.Second) fmt.Println(c.Value("somekey"))}while - for
package main
import ( "fmt" "math" "time")
func Sqrt(x float64) float64 { z := 1.0 for { z -= (z*z - x) / (2 * z) fmt.Println(z) time.Sleep(100000000) }}
func main() { fmt.Println(math.Sqrt(2)) Sqrt(2)}slice
https://blog.go-zh.org/go-slices-usage-and-internals
package main
import "golang.org/x/tour/pic"
func Pic(dx, dy int) [][]uint8 { res := make([][]uint8, dy) for i := 0; i < dy; i++ { res[i] = make([]uint8, dx) for j := 0; j < dx; j++ { res[i][i] = (uint8)(i * j) } } return res}
func main() { pic.Show(Pic)}不过本地打印出来是字符串
map
package main
import ( "golang.org/x/tour/wc" "strings")
func WordCount(s string) map[string]int { res := make(map[string]int) fields := strings.Fields(s) for _, v := range fields { _, ok := res[v] if !ok { res[v] = 1 } else { res[v] += 1 } } return res}
func main() { wc.Test(WordCount)}closure
package main
import "fmt"
func fibonacci() func() int { curr, next := 0, 1 return func() int { res := curr curr = next next = curr + res return res; }}
func main() { f := fibonacci() for i := 0; i < 10; i++ { fmt.Println(f()) }}interface
Stringers
package main
import ( "fmt" "strconv" "strings")
type IPAddr [4]byte
// TODO: 给 IPAddr 添加一个 "String() string" 方法func (ipaddr IPAddr) String() string { ipaddrstr := make([]string, 4) for index, elem := range ipaddr { ipaddrstr[index] = strconv.Itoa(int(elem)) } return strings.Join(ipaddrstr, ".")}
func main() { hosts := map[string]IPAddr{ "loopback": {127, 0, 0, 1}, "googleDNS": {8, 8, 8, 8}, } for name, ip := range hosts { fmt.Printf("%v: %v\n", name, ip) }}实现的接口为
type Stringer interface { String() string}Errors
package main
import ( "fmt" "math")
type ErrNegativeSqrt float64
func (e ErrNegativeSqrt) Error() string { return "cannot Sqrt negative number: " + fmt.Sprint(float64(e))}
func Sqrt(x float64) (float64, error) { if x < 0 { return 0, ErrNegativeSqrt(x) } return math.Sqrt(x), nil}
func main() { fmt.Println(Sqrt(2)) fmt.Println(Sqrt(-2))}实现的接口为
type error interface { Error() string}注意将实现了接口的类型的值赋给接口值
还有 float64 强制类型转换,否则会死循环
Readers
package main
import "golang.org/x/tour/reader"
type MyReader struct{}
// TODO: 给 MyReader 添加一个 Read([]byte) (int, error) 方法func (r MyReader) Read(b []byte) (int, error) { sum := 0 for i := range b { b[i] = 'A' sum++ } return sum, nil}
func main() { reader.Validate(MyReader{})}模仿了 io.Reader 接口的 Read 方法
func (T) Read(b []byte) (n int, err error)rot13Reader
一个 io.Reader 包装另一个 io.Reader,然后通过某种方式修改其数据流
package main
import ( "io" "os" "strings")
type rot13Reader struct { r io.Reader}
func rot13(b byte) byte { // ASCII 65 is A and 90 is Z if b > 64 && b < 91 { b = ((b - 65 + 13) % 26) + 65 } // ASCII 97 is a and 122 is z if b > 96 && b < 123 { b = ((b - 97 + 13) % 26) + 97 } return b}
func (rot *rot13Reader) Read(b []byte) (int, error) { buffer, index := make([]byte, 1), 0 for { _, err := rot.r.Read(buffer) if err == io.EOF { break } b[index] = rot13(buffer[0]) index++ } return index, nil}
func main() { s := strings.NewReader("Lbh penpxrq gur pbqr!") r := rot13Reader{s} io.Copy(os.Stdout, &r)}程序无法终止
Images
package main
import ( "golang.org/x/tour/pic" "image" "image/color")
type Image struct { dx, dy int pic [][]uint8}
func Pic(dx, dy int) [][]uint8 { res := make([][]uint8, dy) for i := 0; i < dy; i++ { res[i] = make([]uint8, dx) for j := 0; j < dx; j++ { res[i][i] = (uint8)(i * j) } } return res}
func (i Image) At(x, y int) color.Color { v := i.pic[x][y] return color.RGBA{v, v, 255, 255}}
func (i Image) Bounds() image.Rectangle { return image.Rect(0, 0, i.dx, i.dy)}
func (i Image) ColorModel() color.Model { return color.RGBAModel}
func main() { const ( dx = 256 dy = 256 ) m := Image{dx, dy, Pic(dx, dy)} pic.ShowImage(m)}实现的接口如下
type Image interface { // ColorModel returns the Image's color model. ColorModel() color.Model // Bounds returns the domain for which At can return non-zero color. // The bounds do not necessarily contain the point (0, 0). Bounds() Rectangle // At returns the color of the pixel at (x, y). // At(Bounds().Min.X, Bounds().Min.Y) returns the upper-left pixel of the grid. // At(Bounds().Max.X-1, Bounds().Max.Y-1) returns the lower-right one. At(x, y int) color.Color}generics
泛型类型
实现一个单链表
package main
import "fmt"
// List represents a singly-linked list that holds// values of any type.type List[T any] struct { next *List[T] val T}
func (list List[T]) push_front(x T) List[T] { new := &List[T]{&list, x} return *new}
func (list *List[T]) pop_front() T { res := list.val *list = *list.next return res}
func (list *List[T]) print() { curr := list for { if curr == nil { break } fmt.Println(curr.val) curr = curr.next }}
func main() { list := List[int]{nil, 1} list = list.push_front(2).push_front(3) list.print() fmt.Println(list.pop_front()) list.print()}存在问题
push_front需要显示返回新的链表pop_front错误处理
当然也有泛型函数
package main
import "fmt"
// Index returns the index of x in s, or -1 if not found.func Index[T comparable](s []T, x T) int { for i, v := range s { // v and x are type T, which has the comparable // constraint, so we can use == here. if v == x { return i } } return -1}
func main() { // Index works on a slice of ints si := []int{10, 20, 15, -10} fmt.Println(Index(si, 15))
// Index also works on a slice of strings ss := []string{"foo", "bar", "baz"} fmt.Println(Index(ss, "hello"))}concurrency
producer - consumer
package main
import "fmt"
var ch = make(chan int, 1)
func producer() { for { ch <- 1 fmt.Print("(") }}
func consumer() { for { <-ch fmt.Print(")") }}
func main() { const n = 2 for i := 0; i < n; i++ { go producer() } consumer()}似乎没有阻塞啊
小心 fatal error: all goroutines are asleep - deadlock!
Equivalent Binary Trees
就是一个中序遍历
package main
import ( "fmt" "golang.org/x/tour/tree")
const N = 10
// Walk 步进 tree t 将所有的值从 tree 发送到 channel ch。func Walk(t *tree.Tree, ch chan int) { if t.Left != nil { Walk(t.Left, ch) }
ch <- t.Value
if t.Right != nil { Walk(t.Right, ch) }}
// Same 检测树 t1 和 t2 是否含有相同的值。func Same(t1, t2 *tree.Tree) bool { ch1 := make(chan int, N) ch2 := make(chan int, N)
go Walk(t1, ch1) go Walk(t2, ch2)
for i := 0; i < N; i++ { if <-ch1 != <-ch2 { return false } }
return true}
func main() { fmt.Println(Same(tree.New(1), tree.New(1))) fmt.Println(Same(tree.New(1), tree.New(2)))}Web Crawler
虚假的爬虫
package main
import ( "fmt" "sync")
type Fetcher interface { // Fetch 返回 URL 的 body 内容,并且将在这个页面上找到的 URL 放到一个 slice 中。 Fetch(url string) (body string, urls []string, err error)}
var mux = sync.Mutex{}var res = make(map[string]string)
func thread(url string, depth int, fetcher Fetcher) { if depth <= 0 { return }
body, urls, err := fetcher.Fetch(url) if err != nil { return }
mux.Lock() if res[url] == "" { res[url] = body } mux.Unlock()
for _, u := range urls { thread(u, depth-1, fetcher) }
return}
// Crawl 使用 fetcher 从某个 URL 开始递归的爬取页面,直到达到最大深度。func Crawl(url string, depth int, fetcher Fetcher) { // TODO: 并行的抓取 URL。 // TODO: 不重复抓取页面。 for i := 0; i < 10; i++ { thread(url, depth, fetcher) }}
func main() { defer func() { for _, elem := range res { fmt.Println(elem) } }() Crawl("https://golang.org/", 4, fetcher)}
// fakeFetcher 是返回若干结果的 Fetcher。type fakeFetcher map[string]*fakeResult
type fakeResult struct { body string urls []string}
func (f fakeFetcher) Fetch(url string) (string, []string, error) { if res, ok := f[url]; ok { return res.body, res.urls, nil } return "", nil, fmt.Errorf("not found: %s", url)}
// fetcher 是填充后的 fakeFetcher。var fetcher = fakeFetcher{ "https://golang.org/": &fakeResult{ "The Go Programming Language", []string{ "https://golang.org/pkg/", "https://golang.org/cmd/", }, }, "https://golang.org/pkg/": &fakeResult{ "Packages", []string{ "https://golang.org/", "https://golang.org/cmd/", "https://golang.org/pkg/fmt/", "https://golang.org/pkg/os/", }, }, "https://golang.org/pkg/fmt/": &fakeResult{ "Package fmt", []string{ "https://golang.org/", "https://golang.org/pkg/", }, }, "https://golang.org/pkg/os/": &fakeResult{ "Package os", []string{ "https://golang.org/", "https://golang.org/pkg/", }, },}注意需要使用 defer 中打印结果
也许并没有并行
doc
Requirements
==do==
- Your client application must implement the eight functions defined in the Client Application API. Your implementation of these 8 functions should satisfy all of the Design Requirements.
- All of your code must be contained in client.go.
==do not==
- Import additional libraries.
- Spawn other processes.
- Read/write to the file system.
- Create network connections.
Revocation
- After revocation, the client MUST return an error if the revoked user attempts to take action through the Client API on the file, with one exception: the case in which a user calls StoreFile on a file that has been revoked is undefined behavior and will not be tested.
- The revoked user should not be able to learn ANYTHING about the file after their access is revoked (a.k.a. they shouldn’t be able to detect when file contents are updated!)
- The client MUST enforce that the file owner is able to revoke access from users who they directly shared the file with. Any other revocation (i.e. owners revoking users who they did not directly share with, or revocations by non-owners) is undefined behavior and will not be tested.
- Re-sharing a file with a revoked user is undefined behavior and will not be tested.
- …
Cryptographic Functions
小心对 bytes 的要求
非对称加密
- Public Key Encryption
- Digital Signatures -> 256 Bytes
哈希函数
- Hash Function
密钥生成
- Hash-Based Key Derivation Function (HashKDF)
- Password-Based Key Derivation Function (PBKDF)
对称加密
- Symmetric Encryption
- Hash-Based Message Authentication Code (HMAC) -> 64 Bytes
随机数生成
- Random Byte Generator
design
Data Structures
主要的数据结构如下
参考了 [highSparrow/UCB-CS161](https://github.com/highSparrow/UCB-CS161/blob/main/Project 2/proj2/proj2.go)
type User struct { Username string Password string
FileMapping map[string]File
PrivateKey userlib.PKEDecKey // for AcceptInvitation SignKey userlib.DSSignKey // for userdata and CreateInvitation}
type File struct { FileInfoID uuid.UUID SourceKey []byte}
type FileInfo struct { Owner string SharedMapping map[string][]string TotalParts int}
type Invitation struct { FileInfoID uuid.UUID SourceKeyWithSig []byte}Server
Keystore
存储 User 的 verifyKey 和 publicKey
Datastore
- 存储 userdata
其 uuid 如下
uuid.FromBytes( userlib.Argon2Key( []byte(userdata.Password), []byte(salt), // username 16) // uuid must be 16 bytes )利用了 Argon2Key 的慢哈希性质,使得攻击者无法在短时间内通过枚举密码,避免 Offline password guessing
同时引入确定性和唯一性的 salt = username,避免攻击者发起 Amortized guessing attacks
需要强调的是,只要密码泄漏,所有的信息都会泄漏,这无法避免
- 存储 FileInfoID -> fileInfoByteME
具体的,fileInfoByte 的前 64 字节为 fileInfoByteM,并使用 macKey 对剩余部分 fileInfoByteE 进行完整性检查
fileInfoByteE 对 fileInfoByte 使用 encKey 进行加密
macKey 和 encKey 通过 SourceKey 派生
- 存储 FileDataID -> FileDataByteME
对于文件数据的第 部分,其 uuid 为
uuid.FromBytes([]byte(fmt.Sprint(i) + file.FileInfoID.String())[:16])其加密和完整性检查与 fileInfo 一致
- 存储 invitationID -> invitationByte
具体细节见 CreateInvitation 部分
User Authentication
InitUser
生成基本信息填充 User 结构体
填充完后将 userdata 存入 Datastore 中
使用 Digital Signatures 对序列化后的 userdataByte 进行签名
userdataByte 则不加密,主要考虑到攻击者获取 uuid 的难度已经很大了
如果攻击者可以遍历 datastore,就需要考虑加密,因为攻击者可以直接获取 value
GetUser
获取 uuid 并得到 userdataByte 和 userdataSig,验证签名并返回即可
Sync
golang 的指针不太好用
试图让每个 session 的 *User 能够指向同一个对象
然而经过序列化之后似乎做不到
下面是一段示例代码,使用了二级指针也无济于事
package main
import ( "encoding/json" "fmt" "github.com/google/uuid")
var data map[uuid.UUID][]byte = make(map[uuid.UUID][]byte)var fooID uuid.UUID = uuid.New()
type Foo struct { X int Y []byte}
func makeFoo() (res *Foo) { var foo Foo foo.X = 1 foo.Y = append(foo.Y, []byte("hello")...)
fooByte, _ := json.Marshal(&foo) data[fooID] = fooByte
return &foo}
type FooPtr *Foo
func main() { var foo1 FooPtr = makeFoo() foo1ptr := &foo1 fmt.Printf("%p %v\n", *foo1ptr, *foo1ptr)
foo2Byte := data[fooID] var foo2 FooPtr
json.Unmarshal(foo2Byte, &foo2) var foo2ptr *FooPtr = &foo2
fmt.Printf("%p %v\n", *foo2ptr, *foo2ptr)
(*foo1ptr).X = 2 fmt.Printf("%p %v\n", *foo1ptr, *foo1ptr) fmt.Printf("%p %v\n", *foo2ptr, *foo2ptr)}于是考虑显式的进行同步
具体而言,在每个成员函数的开头
// sync userdata userdata, err = GetUser(userdata.Username, userdata.Password) if err != nil { return err }在修改了 userdata 如 FileMapping 后
// update and restore userdata userdata.FileMapping[filename] = file
err = storeUserdata(*userdata) if err != nil { return err }虽然 staff 给出了提示
One final note about sessions: if you do everything cleanly/correctly, multiple user sessions should be supported without any additional work.
但是没有什么思路,只能小心的对用户信息进行同步
更复杂的同步情形见 RevokeAccess 部分
File Storage and Retrieval
StoreFile
需要判断 filename 在 local 的 mapping 中是否存在
如果存在,基本保持 file 和 fileInfo 不变,除了置 TotalParts 为
file.FileInfoID = fileExisted.FileInfoID file.SourceKey = fileExisted.SourceKey
fileInfo.Owner = fileInfoExisted.Owner fileInfo.SharedMapping = fileInfoExisted.SharedMapping fileInfo.TotalParts = 1 // reset to one如果不存在,全部重置
file.FileInfoID = uuid.New() file.SourceKey = userlib.RandomBytes(16)
fileInfo.Owner = userdata.Username fileInfo.SharedMapping = make(map[string][]string) fileInfo.TotalParts = 1然后在 Datastore 中存储 fileData 和 storeFileInfo
具体的加密和完整性检查见 Data Structures 部分
别忘了更新 userdata
AppendToFile
由于文件的各个部分之间是单独存储的
所以只要简单的将 TotalParts 加 ,然后存储 fileData 和 storeFileInfo 即可
这种方案可以保证 AppendToFile 的效率要求
LoadFile
对文件的各个部分 parseFileData 然后拼起来就可以了
parse 部分就是 store 部分的逆过程
File Sharing and Revocation
设计的核心部分
具体的细节参考网站
doc 中的 Revocation 部分对一些内容进行了摘录
CreateInvitation
首先需要明确,分享的内容包括 FileInfoID 和加密后的 SourceKey
通过这两个东西就可以构造 File 对象,并获取 FileInfo 和 FileData
其次,不同分享者之间的 File 对象也并非指向同一个对象,这为 Revocation 提供了后门
这意味着需要对授权的分享者之间同步 File 信息,具体细节见 RevokeAccess 等函数
CreateInvitation 首先使用受邀请者的 publicKey,将对应文件的 SourceKey 加密
然后,使用邀请者的 signKey,对加密信息签名
生成 invitation 结构体并存储在 Datastore 中
最后,更新 SharedMapping
fileInfo.SharedMapping[userdata.Username] = append(fileInfo.SharedMapping[userdata.Username], recipientUsername)注意 SharedMapping 实际上是一个树状结构,只不过使用了 mapping 数据结构进行描述
文件所有者和分享者都可以进行 CreateInvitation
AcceptInvitation
CreateInvitation 的逆过程
使用邀请者的 verifyKey 检查 SourceKey 完整性
然后使用自己的 privateKey 解密 SourceKey
构造 File 对象,更新并存储 userdata 信息
RevokeAccess
最复杂的一个函数
注意只有文件所有者才能发起 RevokeAccess,所有者信息就存储在 FileInfo 中
进行 RevokeAccess 有两个关键步骤
- 更换 FileInfoID 和 SourceKey
- 对仍被授权的用户分发这些信息
先看第一步,需要通过 LoadFile 获取文件内容
并记录过时的 FileInfoID 和 SharedMapping
在 Datastore 中删除 FileData,以便于仍被授权的用户意识到需要同步 File 信息
在 userdata 中删除相应的映射,以便于调用 StoreFile 生成新的文件信息
要注意 userdata 的同步
注意到 Revocation 的级联效应,使用 BFS 重新构造 SharedMapping
再看第二步,为了记录这些信息,需要在 Datastore 存储一个全局数据结构 foo
bad design
其描述如下
old uuid.UUID for fileInfo -> (sharers -> new uuid.UUID for invitation)关键在于,文件所有者需要假借真正邀请者的名义进行 createInvitation,并得到 invitationID
仍被授权的用户只要 Accept 文件所有者的 Invitation 即可完成 File 信息的同步
因为 SharedMapping 已经构造好了,所以 AcceptInvitation 中就不需要更新 SharedMapping 了
golang 不支持函数重载,需要 repeat myself…
Sync
只要检查 FileData 就能够判断文件是否遭遇了 RevokeAccess
在 File Storage and Retrieval 的函数中添加如下代码即可
ok = isFileDataExist(file) if !ok { file, err = userdata.syncFile(filename) if err != nil { return err } }注意到在 sync 之前文件可能遭遇了多次 RevokeAccess
所以仍被授权的用户可能需要多次 AcceptInvitation
为此设计辅助函数 revokeUpdateOnce,解析全局数据结构 foo,试图完成一次同步
直到 revokeUpdateOnce 同步失败,此时有两种可能
- 此时 FileData 存在
代表完成了整个同步过程
- 此时 FileData 不存在
代表没有访问权限
test
command
To test your implementation, run go test -v inside of the client_test directory.
To measure and visualize local test coverage (e.g. how many lines of your implementation your test file hits), you can run these commands in the root folder of your repository:
go test -v -coverpkg ./... ./... -coverprofile cover.outgo tool cover -html=cover.outframework
层次化的测试框架
- Pending -
PSpecify - Skipped -
Skip
note
由于没有 autograder,大部分的测试用例都是自己写的
主要分类如下
- Basic Tests
框架提供的测试用例
- API Tests
根据 Design Requirements,对基本的 API 功能和边界情形进行测试
- Sharing Tests
对 File Sharing and Revocation 部分进行更细致的测试
- Efficiency Test
测试 AppendToFile 的性能
- Malicious Actions
大部分未完成,测试系统是否能够检测出入侵行为
可能与实现高度相关