Info
正则表达式
HW 1
词法分析
HW 2
语法分析
HW 3
- Basic
- Listener & Visitor
  - Listener
  - Visitor
HW 4
- LL(1)
- Climbing
语义分析
HW 5
- struct
- listener
HW 6
- SDT
- Altering the Parse with Semantic Predicates
  - Java enum keyword
  - C++ ambiguous phrases
LLVM IR
中间代码生成
- 控制流语句
- 布尔表达式
HW 7
exam
- 语法制导定义与翻译
- 中间代码生成

Info

正则表达式

字母表 $\Sigma$ 是一个有限的符号集合

字母表 $\Sigma$ 上的串是由 $\Sigma$ 中符号构成的一个有穷序列

串的连接和指数运算

语言是给定字母表 $\Sigma$ 上一个任意的可数的串集合。

语言（集合）的并、连接和闭包（指数）运算

给定字母表 $\Sigma$ ， $\Sigma$ 上的正则表达式由且仅由以下规则定义

空串 $\epsilon$
$\forall a \in \Sigma$
括号
并、连接和闭包

每个正则表达式 $r$ 对应一个正则语言 $L(r)$

举个例子

Σ = {a, b}
L(a|b) = {a, b}
L((a|b)(a|b)) = {aa, ab, ba, bb}
L(a∗) = {ϵ, a, aa, aaa, ...}

正则表达式是语法，正则语言是语义

通过扩展 Metacharacter 和 Character classes，便有了现代的正则表达式

HW 1

Crash Course Computer Science

视频前的总结不错

手写浮点数词法分析器

C Floating-Point Constants

Floating Point Constants

grammar Floating;

floats : float* EOF ;
float : digit suffix? ;

digit : (DIGITS '.' DIGITS exp)
      | (DIGITS '.' DIGITS)
      | ('.' DIGITS exp)
      | ('.' DIGITS)
      | (DIGITS '.' exp)
      | (DIGITS '.')
      | (DIGITS exp)
      ;

suffix : 'f'|'F'|'l'|'L' ;

exp : ('e'|'E') ('+'|'-')? DIGITS ;

DIGITS : [0-9]+ ;
WS : [ \t\r\n]+ -> skip ;

区分大写的 TOKEN 和小写的 rule

不考虑字面量的一元运算符

一些测试

1.2f
1.f
.1f
1e-2f
1.2e+2f
.2e2f
2.e2f

识别所有二进制表示的 3 的倍数

^(0|(1(01*0)*1))*$

可以参考

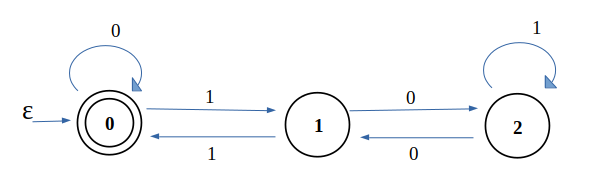
其中状态表示除以 3 的余数，例如除以 3 余 2 时，x = 3y + 2，此时在二进制低位添加一个 1，相当于 x = 2x + 1 = 6y + 5，仍然是除以 3 余 2，同理可以推出其他状态转换关系

将上述 DFA 转换为正则表达式即可

还有一个十进制的，参考正则表达式如何匹配 3 的倍数

词法分析

Automata theory

https://en.wikipedia.org/wiki/Automata_theory

Overview

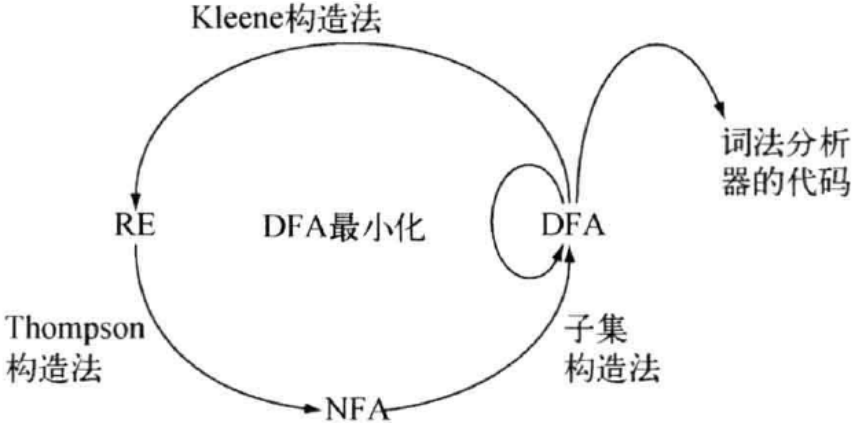
NFA 简洁易于理解，便于描述语言 $L(A)$

DFA 易于判断 $x ∈ L(A)$ , 适合产生词法分析器

RE -> NFA

Thompson 构造法

按结构归纳

NFA -> DFA

子集构造法

DFA minimization

https://en.wikipedia.org/wiki/DFA_minimization

DFA -> 词法分析器

最前优先匹配
最长优先匹配
消除死状态
回溯

DFA -> RE

https://cs.stackexchange.com/questions/2016/how-to-convert-finite-automata-to-regular-expressions

Floyd–Warshall algorithm

HW 2

考虑正则表达式

r = (1|01)^{∗}0^{∗}

使用 $\text{Thompson}$ 构造法构造等价的 $\text{NFA}$

使用子集构造法构造等价的 $\text{DFA}$

NFA State	DFA State	0	1
{1,2,3,6,9,10,12}	A	B	C
{7,10,11,12}	B	D	E
{2,3,4,5,6,9,10,12}	C	B	C
{10,11,12}	D	D	DEAD STATE
{2,3,5,6,8,9,10,12}	E	B	C

将上一步构造的 $\text{DFA}$ 最小化

初始 -> {{A,B,C,D,E},{F}}
考虑 0 -> {{A,C,E},{B,D},{F}}
考虑 1 -> {{A,C,E},{B},{D},{F}}

合并状态 $A,C,E$

语法分析

二义性

if statement

stat : 'if' expr 'then' stat
     | 'if' expr 'then' stat 'else' stat
     | expr
     ;

提取左公因子无助于消除文法二义性

ANTLR 4 可以处理有左公因子的文法，预测分析法则无法处理

一种消除文法二义性的方案如下

stat : matched_stat | open_stat ;

matched_stat : 'if' expr 'then' matched_stat 'else' matched_stat
             | expr
             ;

open_stat: 'if' expr 'then' stat
         | 'if' expr 'then' matched_stat 'else' open_stat
         ;

else 与最近的 if 匹配

结合性与优先级

expr :
  | expr '*' expr
  | expr '-' expr
  | DIGIT
  ;

左递归 (左结合)

// expr : term ('-' term)* ;
expr : expr '-' term
     | term
     ;

// term: factor ('*' factor)* ;
term : term '*' factor
     | factor
     ;

factor : DIGIT ;

右递归 (右结合)

// term - term - term ...
expr : term expr_prime ;
expr_prime : '-' term expr_prime
     |
     ;

// factor * factor * factor ...
term : factor term_prime ;
term_prime : '*' factor term_prime
     |
     ;

factor : DIGIT ;

ANTLR 4 可以处理 (直接) 左递归

expr: ID '(' exprList? ')'    # Call // function call
    | expr '[' expr ']'       # Index // array subscripts
    | op = '-' expr                # Negate // right association
    | op = '!' expr                # Not // right association
    | <assoc = right> expr '^' expr # Power
    | lhs = expr (op = '*'| op = '/') rhs = expr     # MultDiv
    | lhs = expr (op = '+'| op = '-') rhs = expr     # AddSub
    | lhs = expr (op = '==' | op = '!=') rhs = expr  # EQNE
    | '(' expr ')'            # Parens
    | ID                      # Id
    | INT                     # Int
    ;

靠前的产生式优先级越高
默认为左结合，可以指定为右结合
可以为产生式右侧成员命名
可以为产生式命名，用于 visitor 或 listener

上下文无关文法

语法

上下文无关文法 $G$ 是一个四元组 $G = (T, N, P, S)$

$T$ 是终结符号 (Terminal) 集合，对应于词法分析器产生的词法单元
$N$ 是非终结符号 (Non-terminal) 集合
$P$ 是产生式 (Production) 集合

A ∈ N \to α ∈ (T ∪ N)^{∗}

$S$ 为开始 (Start) 符号，要求 $S \in N$ 且唯一

语义

推导 (Derivation) 将某个产生式的左边替换成它的右边

如果 $S \stackrel{*}{\Rightarrow} α$ , 且 $α ∈ (T ∪ N)^{∗}$ , 则称 $α$ 是文法 $G$ 的一个句型

如果 $S \stackrel{*}{\Rightarrow} w$ , 且 $w ∈ T^{∗}$ , 则称 $w$ 是文法 $G$ 的一个句子

上下文无关文法 $G$ 的语言 $L(G)$ 是它能推导出的所有句子构成的集合

LL(1)

first & follow
预测分析表

ANTLR

ANTLR 4 是如何处理直接左递归与优先级的

优先级上升算法

ANTLR 4 是如何进行错误报告与恢复的

参考 ANTLR 4 权威指南 CHAPTER 9 Error Reporting and Recovery

ANTLR 4 使用了一种名为 Adaptive LL(∗) 的新技术

三篇论文

例如，对于如下文法

P = \{S \to Ac \vert Ad, A \to aA \vert b \}

不是 LL(*) 文法，因为不知道需要向前看多少个 $a$

Adaptive LL(∗) 的核心思想是利用 ATN (Augmented Transition Network)，动态构建 lookahead DFA

例如对于上述文法，其对应的 ATN 如下

在 $P_S$ 状态以及输出 $bc$ 和 $bd$ 下，其动态构建的 lookahead DFA 如下

这里的三元组含义为 (状态, 选择的产生式编号, 栈)

当 ATN 的边为非终结符时，就会递归搜索对应的 ATN，同时递归返回时的状态压入栈中

当 DFA 的 state 中所有的三元组选择的产生式编号相同时，例如 $f_1$ 和 $f_2$ ，就可以确定使用哪一条产生式

更多细节可参考第三篇论文

HW 3

Basic

考虑上下文无关文法

S \to SS+ | SS∗ | a

以及串 $aa + a∗$

一棵语法分析树如下

graph TB A["S"] --> B["S"] A["S"] --> C["S"] A["S"] --> D["*"] B["S"] --> E["S"] B["S"] --> F["S"] B["S"] --> G["+"] E["S"] --> H["a"] F["S"] --> I["a"] C["S"] --> J["a"]

该文法不是二义性文法

可以证明该文法为 $\text{SLR}$ 文法，因而不是二义性文法

或者

\begin{array}{l} L(SS+) \cap L(SS*) = \varnothing \newline L(SS+) \cap L(a) = \varnothing \newline L(SS*) \cap L(a) = \varnothing \newline \end{array}

该文法生成的语言为

只含有 $a$ 及加法和乘法的后缀表达式

Listener & Visitor

The biggest difference between the listener and visitor mechanisms is that listener methods are called independently by an ANTLR-provided walker object, whereas visitor methods must walk their children with explicit visit calls. Forgetting to invoke visitor methods on a node’s children, means those subtrees don’t get visited.

考虑如下的文法文件，命名为 SysYParser.g4

program : compUnit;
compUnit : EOF;

Listener

ANTLR library 中定义了下述接口

public interface ParseTreeListener {
    void visitTerminal(TerminalNode var1);
    void visitErrorNode(ErrorNode var1);
    void enterEveryRule(ParserRuleContext var1);
    void exitEveryRule(ParserRuleContext var1);
}

ANTLR 会根据文法文件生成如下三个文件

SysYParserListener

生成一个新的接口，该接口继承了 ParseTreeListener，并对每一个非终结符生成 enterXXX 和 exitXXX 方法

public interface SysYParserListener extends ParseTreeListener {
  void enterProgram(SysYParser.ProgramContext ctx);
  void exitProgram(SysYParser.ProgramContext ctx);
  void enterCompUnit(SysYParser.CompUnitContext ctx);
  void exitCompUnit(SysYParser.CompUnitContext ctx);
}

SysYParserBaseListener

SysYParserListener 接口的默认实现，其方法均为空

SysYParser

其中会为每一个非终结符定义静态类 XXXContext，其中的 enterRule 和 exitRule 会调用上述对应的接口方法

public static class ProgramContext extends ParserRuleContext {
    @Override
    public void enterRule(ParseTreeListener listener) {
      if ( listener instanceof SysYParserListener ) ((SysYParserListener)listener).enterProgram(this);
    }
    @Override
    public void exitRule(ParseTreeListener listener) {
      if ( listener instanceof SysYParserListener ) ((SysYParserListener)listener).exitProgram(this);
    }
}

对应的类关系如下

ProgramContext -> ParserRuleContext -> RuleContext -> RuleNode -> ParseTree -> SyntaxTree -> Tree

listener 的驱动类为 ParseTreeWalker

public void walk(ParseTreeListener listener, ParseTree t) {
    if (t instanceof ErrorNode) {
      listener.visitErrorNode((ErrorNode)t);
    } else if (t instanceof TerminalNode) {
      listener.visitTerminal((TerminalNode)t);
    } else {
        RuleNode r = (RuleNode)t;
        this.enterRule(listener, r);
        int n = r.getChildCount();
        for (int i = 0; i < n; ++i) {
          this.walk(listener, r.getChild(i));
        }
        this.exitRule(listener, r);
    }
}

其中的 walk 方法会根据给定的 listener 以 DFS 的顺序调用 enterRule 和 exitRule

protected void enterRule(ParseTreeListener listener, RuleNode r) {
    ParserRuleContext ctx = (ParserRuleContext)r.getRuleContext();
    listener.enterEveryRule(ctx);
    ctx.enterRule(listener);
}

最终调用到 XXXContext 类定义的 enterRule 和 exitRule

Visitor

ANTLR library 中定义了下述接口

public interface ParseTreeVisitor<T> {
    T visit(ParseTree var1);
    T visitChildren(RuleNode var1);
    T visitTerminal(TerminalNode var1);
    T visitErrorNode(ErrorNode var1);
}

ANTLR 会根据文法文件生成如下三个文件

SysYParserVisitor

生成一个新的接口，该接口继承了 ParseTreeVisitor，并对每一个非终结符生成 visitXXX 方法

public interface SysYParserVisitor<T> extends ParseTreeVisitor<T> {
  T visitProgram(SysYParser.ProgramContext ctx);
  T visitCompUnit(SysYParser.CompUnitContext ctx);
}

SysYParserBaseVisitor

SysYParserListener 接口的默认实现，仅调用 visitChildren 方法

public class SysYParserBaseVisitor<T> extends AbstractParseTreeVisitor<T> implements SysYParserVisitor<T> {
  @Override public T visitProgram(SysYParser.ProgramContext ctx) { return visitChildren(ctx); }
  @Override public T visitCompUnit(SysYParser.CompUnitContext ctx) { return visitChildren(ctx); }
}

其中 AbstractParseTreeVisitor 实现了 ParseTreeVisitor 接口中的方法，visitChildren 实现如下

public T visitChildren(RuleNode node) {
    T result = this.defaultResult();
    int n = node.getChildCount();
    for (int i = 0; i < n && this.shouldVisitNextChild(node, result); ++i) {
        ParseTree c = node.getChild(i);
        T childResult = c.accept(this);
        result = this.aggregateResult(result, childResult);
    }
    return result;
}

注意到其实现中的 accept 调用，该接口定义在 ParseTree 中

<T> T accept(ParseTreeVisitor<? extends T> var1);

其默认实现在 RuleContext 中

public <T> T accept(ParseTreeVisitor<? extends T> visitor) {
  return visitor.visitChildren(this);
}

SysYParser

其中会为每一个非终结符定义静态类 XXXContext，并 override 掉 accept 的实现

public static class ProgramContext extends ParserRuleContext {
    @Override
    public <T> T accept(ParseTreeVisitor<? extends T> visitor) {
        if ( visitor instanceof SysYParserVisitor ) return ((SysYParserVisitor<? extends T>)visitor).visitProgram(this);
        else return visitor.visitChildren(this);
    }
}

于是可以通过继承 SysYParserBaseVisitor 的方式来 override visitProgram 的默认实现，从而改变 accept 时的行为

listener 的驱动类为 AbstractParseTreeVisitor

public T visit(ParseTree tree) {
  return tree.accept(this);
}

其中的 visit 方法会在树根处调用 accept 方法，配合 visitChildren 的默认语义，实现以 DFS 的顺序调用各非终结符的 visitXXX 方法

HW 4

LL(1)

\begin{array}{l} S \to BAS \newline S \to cA \newline A \to aA \newline A \to e \newline B \to bB \newline B \to \epsilon \newline \end{array}

给出各非终结符的 $first$ 和 $follow$ 集合

\begin{array}{l} first(S) = \{b,a,e,c\} \newline first(A) = \{a,e\} \newline first(B) = \{b,\epsilon\} \newline follow(S) = \{\$\} \newline follow(A) = \{\$,b,a,e,c\} \newline follow(B) = \{a,e\} \newline \end{array}

预测分析表如下

	$a$	$b$	$c$	$e$
$S$	$S \to BAS$	$S \to BAS$	$S \to cA$	$S \to BAS$
$A$	$A \to aA$			$A \to e$
$B$	$B \to \epsilon$	$B \to bB$		$B \to \epsilon$

无冲突，为 $\text{LL(1)}$ 文法

参考工具推荐 https://www.jflap.org/

Climbing

stat : expr[0] ';' EOF;

expr[int _p]
    : (  INT
       | ID
      )
      (  {4 >= $_p}? '*' expr[5]
       | {3 >= $_p}? '+' expr[4]
      )*
    ;

给出 $1 ∗ 2 + 3 + 4 ∗ 5$ 在该文法下对应的语法分析树

graph TB A["stat"] --> B["expr[0]"] A --> C[";"] A --> D["EOF"] B --> E["ID"] E --> F["1"] B --> G["*"] B --> H["expr[5]"] H --> I["ID"] I --> J["2"] B --> K["+"] B --> L["expr[4]"] L --> M["ID"] M --> N["3"] B --> O["+"] B --> P["expr[4]"] P --> Q["ID"] Q --> R["4"] P --> S["*"] P --> T["expr[5]"] T --> U["ID"] U --> V["5"]

在 ANTLR 中，其原始文法为

stat : expr ';' EOF;

expr : expr '*' expr
     | expr '+' expr
     | INT
     | ID
     ;

对于 expr 规则，越往上的产生式其优先级越高，可以为每一条产生式赋予一个优先级

expr : expr '*' expr (4)
     | expr '+' expr (3)
     | INT           (2)
     | ID            (1)
     ;

对于直接左递归，即前两条产生式，会将其重写为有条件的迭代形式，其条件便于其优先级相关

对于右递归，例如下述文法 expr 规则的第一条产生式

stat : expr ';' EOF;

expr : '-' expr       (4)
     | expr '!'       (3)
     | expr '+' expr  (2)
     | ID             (1)
     ;

ANTLR 会改写为如下形式

stat : expr[0] ';' EOF;

expr[int _p]
    : (   ID
        | '-' expr[4]
      )
      (   {3 >= $_p}? '!'
        | {2 >= $_p}? '+' expr[3]
      )*
     ;

对于指定了结合性的递归规则，例如下述文法 expr 规则的第一条产生式

stat : expr ';' EOF ;
expr : <assoc = right> expr '^' expr
     | expr '+' expr
     | INT
     ;

ANTLR 会改写为如下形式

stat : expr[0] ';' EOF;

expr[int _p]
    : ( INT )
      (   {3 >= $_p}? '^' expr[3]
        | {2 >= $_p}? '+' expr[3]
      )*
     ;

总结如下

For left-associative operators, the right operand gets one more precedence level than the operator itself.
For right-associative operators, the right operand gets the same precedence level as the current operand.

更多内容可以参考论文 Adaptive LL(*) Parsing: The Power of Dynamic Analysis 的 Appendix C: Left-recursion Elimination

语义分析

符号表

struct 和 function 既是 symbol 又是 scope

参考实现 https://github.com/antlr/symtab

类型系统

类型检查
类型转换
类型综合

根据子表达式的类型确定表达式的类型

类型推导

根据某语言结构的使用方式确定表达式的类型

C++ 中的 auto 关键字

https://www.youtube.com/watch?v=SWTWkYbcWU0

属性文法 (Attribute Grammar)

为上下文无关文法赋予语义

实践

Offline

按照从左到右的深度优先顺序遍历语法分析树，在合适的时机执行合适的动作，计算相应的属性值

Listener & Visitor

Online

一个动作在它左边的所有文法符号都处理过之后立刻执行

B → X\{a\}Y

可以参考 The Definitive ANTLR 4 Reference 的 chapter 10

尽管提升了效率，但牺牲了可读性，文法和语义形成了耦合，故不推荐

https://github.com/antlr/antlr4/blob/master/doc/faq/general.md#what-is-the-difference-between-antlr-3-and-4

理论

语法制导定义 (Syntax-Directed Definition; SDD)

SDD 是一个上下文无关文法和属性及规则的结合

注释 (annotated) 语法分析树

显示了各个属性值的语法分析树

在 ANTLR 中可以使用 ParseTreeProperty

综合属性 (Synthesized Attribute)

节点 N 上的综合属性只能通过 N 的子节点或 N 本身的属性来定义

S 属性定义 (S-Attributed Definition)

如果一个 SDD 的每个属性都是综合属性，则它是 S 属性定义

S 属性定义的依赖图描述了属性实例之间自底向上的信息流

此类属性值的计算可以在自顶向下的 LL 语法分析过程中实现

继承属性 (Inherited Attribute)

节点 N 上的继承属性只能通过 N 的父节点、N 本身和 N 的兄弟节点上的属性来定义

L 属性定义 (L-Attributed Definition)

如果一个 SDD 的每个属性要么是综合属性，要么是继承属性，但是它的规则满足某些限制 (left)，则它是 L 属性定义

语法制导的翻译方案 (Syntax-Directed Translation Scheme; SDT)

SDT 是在其产生式体中嵌入语义动作的上下文无关文法

如何将带有语义规则的 SDD 转换为带有语义动作的 SDT

S 属性定义

后缀翻译方案：所有动作都在产生式的最后

L 属性定义

A \to X_1 \cdots X_i \cdots X_n

原则：从左到右处理各个 $X_i$ 符号，对每个 $X_i$ , 先计算继承属性，后计算综合属性

(左递归) S 属性定义 -> (右递归) L 属性定义

略

HW 5

struct

略微修改程序，以符合 C 语言语义

struct A {
    int x;
    struct B { int y; };
    struct B b;
    struct C { int z; };
    struct C c;
};

struct A a;

void f() {
    struct D {
        int i;
    };
    struct D d;
    d.i = a.b.y;
}

在 Cymbol 文法基础上，struct 结构的文法描述如下

prog : (varDecl | functionDecl | structDecl)* EOF ;

varDecl : type ID ('=' expr)? ';' ;

type : 'int' | 'double' | 'void' | structType ;

structDecl : 'struct' ID '{' (varDecl | structDecl)* '}' ';' ;
structType : 'struct' ID ;

stat : structDecl | ... ;
expr : expr '.' ID | ... ;

其中 stat 和 expr 规则仅给出了增量的部分，注意结构体成员访问运算符的优先级介于数组下标运算符和一元运算符之间

参考 C Operator Precedence

上述程序在新的文法下，语法树结构为

此处忽略了匿名结构体的的语法定义，例如下述程序

struct {
  int x;
} a;

下面考虑构建 struct 作用域

enterStructDecl 开始新的 struct 作用域
exitStructDecl 退出 struct 作用域
struct 对应的 symbol 应置入其作用域的 enclosing 作用域中
解析结构体成员访问运算符时，应先在符号表中 resolve 结构体变量对应的 symbol 和 scope，然后在这个 scope 中 resolve 结构体成员，该过程可递归进行

listener

将产生式改写为如下文法文件

program : type dec
        ;

type : 'int'      # TypeInt
     | 'float'    # TypeFloat
     ;

dec : dec ',' ID  # DecMore
    | ID          # DecOne
    ;

对应的 listener 实现如下

package org.example.hw5;

import org.antlr.v4.runtime.tree.ParseTreeProperty;

public class HW5DerivedListener extends HW5BaseListener {
    private final ParseTreeProperty<String> typeProperty = new ParseTreeProperty<>();

    @Override
    public void enterTypeInt(HW5Parser.TypeIntContext ctx) {
        typeProperty.put(ctx.getParent(), "int");
    }

    @Override
    public void enterTypeFloat(HW5Parser.TypeFloatContext ctx) {
        typeProperty.put(ctx.getParent(), "float");
    }

    @Override
    public void enterDecMore(HW5Parser.DecMoreContext ctx) {
        System.err.printf("+ %s %s%n", typeProperty.get(ctx.getParent()), ctx.ID().getSymbol().getText());
        typeProperty.put(ctx, typeProperty.get(ctx.getParent()));
    }

    @Override
    public void enterDecOne(HW5Parser.DecOneContext ctx) {
        System.err.printf("+ %s %s%n", typeProperty.get(ctx.getParent()), ctx.ID().getSymbol().getText());
    }
}

简单起见，使用字符串表示类型

对于输入 int a, b, c，对应的输出为

+ int c
+ int b
+ int a

尝试使用 Gradle 构建 ANTLR，发现似乎不支持分开写 lexer grammar 和 parser grammar

使用 lexer grammar 和 parser grammar 时，有些语法似乎不再支持，例如对比

https://github.com/lukekras/def-antlr4-ref-code/blob/c21fc72811e29da7438bdcecfed7807391f41bc8/code/lexmagic/Cymbol.g4#L6

https://github.com/lukekras/def-antlr4-ref-code/blob/master/code/lexmagic/CymbolLexer.g4#L3

HW 6

SDT

将产生式改写为如下文法文件

program : dec
        ;

dec : dec ';' dec
    | type ID
    | 'func' ID '{' dec '}'
    ;

type : 'int'
     ;

打印程序 P 一共声明了多少个 id

翻译方案如下

program : dec { System.err.println($dec.out); }
        ;

dec returns [int out]
@init {
    $out = 0;
}
: left = dec ';' right = dec { $out += $left.out + $right.out; }
    | type ID { $out += 1; }
    | 'func' ID '{' dec '}' { $out += 1 + $dec.out; }
    ;

type : 'int'
     ;

测试输入

int id ; func id {int id ; func id {int id}}

测试输出

打印程序 P 中每个变量 id (不考虑函数名 id) (在 {} 中) 的嵌套深度

由于 ANTLR 不支持为立即左递归的非终结符提供参数，所以考虑消除立即左递归，消除后的文法如下

program : dec
        ;

dec : type ID dec1?
    | 'func' ID '{' dec '}' dec1?
    ;

dec1 : ';' dec
     ;

type : 'int'
     ;

此时，翻译方案如下

program : dec[0]
        ;

dec[int depth]
: type ID { System.err.printf("%d %d%n", $ID.getTokenIndex(), depth); } dec1[depth]?
    | 'func' ID '{' dec[depth + 1] '}' dec1[depth]?
    ;

dec1[int depth]
: ';' dec[depth]
     ;

type : 'int'
     ;

测试输入

int id ; func id {int id ; func id {int id} ; int id}

测试输出

其中每一行的第一个分量代表 token index，第二个分量代表嵌套深度

Altering the Parse with Semantic Predicates

The Definitive ANTLR 4 Reference chapter 11

这一节用了两个例子介绍 semantic predicates

Java enum keyword
C++ ambiguous phrases

Java `enum` keyword

在 Java 5 之前 enum 并不是 keyword，为了解析不同版本的 Java 代码，需要使用 semantic predicates

有两种方案

在词法分析阶段处理

@lexer::members { public static boolean java5 = false ;}

ENUM : 'enum' {java5}? ; // must be before ID
ID   : [a-zA-Z]+ ;

此处 java5 作为词法分析阶段的 public 成员变量，若为 false，则 'enum' 被识别为 ID，反之被识别为 ENUM

另一种可行的方案是利用 actions

tokens { ENUM }

ID : [a-zA-Z]+ { if (java5 && getText().equals("enum")) setType(Enum2Parser.ENUM); } ;

该方案可在 Lab 1 中使用

DECIMAL_INT_CONST : NON_ZERO_DIGIT DIGIT* { setType(INTEGR_CONST); } ;
OCTAL_INT_CONST : '0' OCTAL_DIGIT* { setText(NumberUtils.octToDec(getText())); setType(INTEGR_CONST); } ;
HEXADECIMAL_INT_CONST : HEXADECIMAL_PREFIX HEXADECIMAL_DIGIT+ { setText(NumberUtils.hexToDec(getText())); setType(INTEGR_CONST); } ;

INTEGR_CONST : DECIMAL_INT_CONST | OCTAL_INT_CONST | HEXADECIMAL_INT_CONST ;

在语法分析阶段处理

@parser::members { public static boolean java5; }

enumDecl
    :   {java5}? 'enum' id '{' id (',' id)* '}'
    ;

id  :   ID
    |   {!java5}? 'enum'
    ;

此处 java5 作为语法分析阶段的 public 成员变量，若为 false，则相当于抑制了 enumDecl 这条规则

C++ ambiguous phrases

C++ 中存在着大量的二义性文法，为了消除二义性，需要一些额外的上下文信息，甚至一些硬性的规定

下面举一个例子，对于表达式 T(i)

若 T 为函数名，则为函数调用
若 T 为类型名，则可能为显式类型转换
- 或者变量声明，等同于 T i，此时 i 为变量名

可以通过使用 semantic predicates，区分 T 为函数名和类型名这条分支，这需要利用上下文信息

由于 C++ 允许 forward references，所以可能当解析到 T(i) 时，T 的类型信息并不完整，这就需要 multiple passes

但即使了解到 T 为类型名，该表达式仍然存在二义性，为此 C++ 在标准中规定 declarations 优先于 expressions

LLVM IR

带有类型的、介于高级程序设计语言与汇编语言之间

intro

示例程序如下

int factorial(int val);

int main(int argc, char **argv) {
  return factorial(2) * 7 == 42;
}

使用 clang 显示抽象语法树

> clang -Xclang -ast-dump -c a.c
TranslationUnitDecl 0x555ad2030c38 <<invalid sloc>> <invalid sloc>
|-TypedefDecl 0x555ad2031460 <<invalid sloc>> <invalid sloc> implicit __int128_t '__int128'
| `-BuiltinType 0x555ad2031200 '__int128'
|-TypedefDecl 0x555ad20314d0 <<invalid sloc>> <invalid sloc> implicit __uint128_t 'unsigned __int128'
| `-BuiltinType 0x555ad2031220 'unsigned __int128'
|-TypedefDecl 0x555ad20317d8 <<invalid sloc>> <invalid sloc> implicit __NSConstantString 'struct __NSConstantString_tag'
| `-RecordType 0x555ad20315b0 'struct __NSConstantString_tag'
|   `-Record 0x555ad2031528 '__NSConstantString_tag'
|-TypedefDecl 0x555ad2031870 <<invalid sloc>> <invalid sloc> implicit __builtin_ms_va_list 'char *'
| `-PointerType 0x555ad2031830 'char *'
|   `-BuiltinType 0x555ad2030ce0 'char'
|-TypedefDecl 0x555ad2031b68 <<invalid sloc>> <invalid sloc> implicit __builtin_va_list 'struct __va_list_tag[1]'
| `-ConstantArrayType 0x555ad2031b10 'struct __va_list_tag[1]' 1
|   `-RecordType 0x555ad2031950 'struct __va_list_tag'
|     `-Record 0x555ad20318c8 '__va_list_tag'
|-FunctionDecl 0x555ad2087160 <a.c:1:1, col:22> col:5 used factorial 'int (int)'
| `-ParmVarDecl 0x555ad2087090 <col:15, col:19> col:19 val 'int'
`-FunctionDecl 0x555ad20873f0 <line:3:1, line:5:1> line:3:5 main 'int (int, char **)'
  |-ParmVarDecl 0x555ad2087268 <col:10, col:14> col:14 argc 'int'
  |-ParmVarDecl 0x555ad2087310 <col:20, col:27> col:27 argv 'char **'
  `-CompoundStmt 0x555ad20875d8 <col:33, line:5:1>
    `-ReturnStmt 0x555ad20875c8 <line:4:3, col:30>
      `-BinaryOperator 0x555ad20875a8 <col:10, col:30> 'int' '=='
        |-BinaryOperator 0x555ad2087568 <col:10, col:25> 'int' '*'
        | |-CallExpr 0x555ad2087520 <col:10, col:21> 'int'
        | | |-ImplicitCastExpr 0x555ad2087508 <col:10> 'int (*)(int)' <FunctionToPointerDecay>
        | | | `-DeclRefExpr 0x555ad20874a0 <col:10> 'int (int)' Function 0x555ad2087160 'factorial' 'int (int)'
        | | `-IntegerLiteral 0x555ad20874c0 <col:20> 'int' 2
        | `-IntegerLiteral 0x555ad2087548 <col:25> 'int' 7
        `-IntegerLiteral 0x555ad2087588 <col:30> 'int' 42

生成 LLVM IR (无优化)

> clang -S -emit-llvm a.c -O0

a.ll 文件的部分内容如下

define dso_local i32 @main(i32 noundef %0, i8** noundef %1) #0 {
  %3 = alloca i32, align 4
  %4 = alloca i32, align 4
  %5 = alloca i8**, align 8
  store i32 0, i32* %3, align 4
  store i32 %0, i32* %4, align 4
  store i8** %1, i8*** %5, align 8
  %6 = call i32 @factorial(i32 noundef 2)
  %7 = mul nsw i32 %6, 7
  %8 = icmp eq i32 %7, 42
  %9 = zext i1 %8 to i32
  ret i32 %9
}

declare i32 @factorial(i32 noundef) #1

几个要点

@ 开头的符号为全局符号，% 开头的符号为局部符号
LLVM IR 为静态单赋值 (SSA) 形式，即要求每个变量只分配一次，并且每个变量在使用之前定义
- 例如 %7 = mul nsw i32 %6, 7 的左侧不可以复用 %6
注意 i32 等类型标识，i8** 表示 char**，布尔值类型为 i1
main 函数的前六行指令操作内存，由于未被使用，在更高的优化等级下会被优化掉

branch and phi

示例程序如下

int factorial(int val) {
  if (val == 0) {
    return 1;
  }

  return val * factorial(val - 1);
}

int main(int argc, char **argv) {
  return factorial(2) * 7 == 42;
}

生成 LLVM IR，无优化并抑制 optnone 属性

> clang -Xclang -disable-O0-optnone -S -emit-llvm a.c

参考 https://stackoverflow.com/questions/67393329/llvm-doesnt-generate-cfg

根据 .ll 文件生成 .dot 文件

> opt -dot-cfg a.ll -disable-output

对应的 cfg 如下

由于 SSA 形式的限制，对于不同分支下的相同变量，例如 return 的返回值，考虑将其存储在相同的内存位置，然后在 return 的时候读取即可

在更高的优化等级下，会将分支转换为带有 phi 函数的 IR，例如

> clang -S -emit-llvm a.c -O1

对应的 cfg 如下

注意 %8 = phi i32 [ %6, %3 ], [ 1, %1 ] 这一行，代表若为 %3 分支，则取值为 %6，若为 %1 分支，则取值为 1

关于 phi 函数的内部实现，可以参考 https://mapping-high-level-constructs-to-llvm-ir.readthedocs.io/en/latest/control-structures/ssa-phi.html

kaleidoscope

https://llvm.org/docs/tutorial/

https://github.com/ghaiklor/llvm-kaleidoscope

https://github.com/courses-at-nju-by-hfwei/kaleidoscope-in-java

中间代码生成

综合属性 E.code 中间代码
继承属性 B.true, B.false, S.next 指明了控制流跳转目标

控制流语句

布尔表达式

可能的上下文

布尔值
控制流跳转

建议在语法阶段区别上述两种上下文，这里仅考虑控制流跳转

注意这里的短路求值特性

or B1.true = B.true
and B1.false = B.false

HW 7

将如下代码片段翻译成中间代码

while (x > 1) {
    if (x < 3) {
        x = 5;
    } else {
        if (x < 5) {
            x = 7;
        }
    }
}

中间代码如下

L1:  if x > 1 goto L2
     goto L3
L2:  if x < 3 goto L4
     goto L5
L4:  X = 5
     goto L7
L5:  if x < 5 goto L6
     goto L7
L6:  x = 7
L7:  goto L1
L3:

exam

语法制导定义与翻译

考虑如下文法 G

S → (L) | a
L → L, S | S

请设计语法制导的翻译方案，完成下列任务

你需要自行定义合适的属性

计算每个 a 的嵌套深度。例如，在句子 (a, (a, a)) 中，每个 a 的嵌套深度分别为 1, 2, 2

定义 .D 为嵌套深度

S → { L.D = S.D + 1 } (L)
S → a { print(S.D) }
L → { L1.D = L.D } L1, { S.D = L.D } S
L → { S.D = L.D } S

计算每个 a 的位置。例如，在句子 (a, (a, (a, a), (a))) 中，每个 a 的位置分别为 2, 5, 8, 10, 14

定义 .O 为起始位置偏移，.L 为长度

S → { L.O = S.O + 1 } (L) { S.L = L.L + 2 }
S → a { print(S.O); S.L = 1 }
L → { L1.O = L.O } L1, { S.O = L1.O + L1.L + 1 } S { L.L = L1.L + S.L + 1 }
L → { S.O = L.O } S { L.L = S.L }

中间代码生成

考虑循环语句

S → do S1 while B

请基于控制流语句与布尔表达式语法制导定义，为上述语句添加语义规则

Production                  Syntax Rule

S -> do S1 while B          S1.next = newlabel()
                            B.true = newlabel()
                            B.false = S.next
                            S.code = label(B.true) || S1.code || label(S1.next) || B.code || gen('goto', B.true)

补充 for 循环

Production                  Syntax Rule

S -> for (S1; B; S2) S3     S1.next = newlabel()
                            B.true = newlabel()
                            B.false = S.next
                            S2.next = S1.next
                            S3.next = newlabel()
                            S.code = S1.code
                                || lable(S1.next) || B.code
                                || lable(B.true) || S3.code
                                || label(S3.next) || S2.code
                                || gen('goto', S1.next)

参考 https://github.com/fool2fish/dragon-book-exercise-answers/blob/master/ch06/6.6/6.6.md

请为以下代码片段生成中间代码

do {
    if (i == 2021) {
        print('hello');
    }
    i = i + 1;
} while (i > 2000 && i < 3000);

中间代码如下

L1:  if i == 2021 goto L5
     goto L6
L5:  print
L6:  i = i + 1
L2:  if i > 2000 goto L4
     goto L3
L4:  if i < 3000 goto L1
     goto L3
L3:

编译原理 whf

TOC

Info

正则表达式

HW 1

Crash Course Computer Science

手写浮点数词法分析器

识别所有二进制表示的 3 的倍数

词法分析

Automata theory

Overview

RE -> NFA

NFA -> DFA

DFA minimization

DFA -> 词法分析器

DFA -> RE

HW 2

语法分析

二义性

结合性与优先级

上下文无关文法

语法

语义

LL(1)

ANTLR

HW 3

Basic

Listener & Visitor

Listener

Visitor

HW 4

LL(1)

Climbing

语义分析

符号表

类型系统

属性文法 (Attribute Grammar)

实践

理论

HW 5

struct

listener

HW 6

SDT

Altering the Parse with Semantic Predicates

Java enum keyword

C++ ambiguous phrases

LLVM IR

intro

branch and phi

kaleidoscope

中间代码生成

控制流语句

布尔表达式

HW 7

exam

语法制导定义与翻译

中间代码生成

Java `enum` keyword