TOC
Open TOC
大纲
计算机系统概述
W 1 / 2
Y 1
- 概念
- 计算机,组织,结构
- 计算机发展历史
- 冯 · 诺伊曼结构,摩尔定律
- 计算机发展
- 基本功能,运算速度
- 计算机性能
- CPU 性能评价
计算机
通用电子数字计算机:
- 通用:不是一种专用设备
- 电子:采用电子元器件
- 数字:信息采用数字化的形式表示
组织与结构
- 组织(Organization):对编程人员不可见
操作单元及其相互连接
包括:控制信号,存储技术,……
例如:实现乘法是通过硬件单元还是重复加法?
- 结构(Architecture):对编程人员可见
直接影响程序逻辑执行的属性
包括:指令集,表示数据类型的位数,…
例如:是否有乘法指令?
冯 · 诺伊曼结构
-
二进制
-
存储程序
-
五个组成部分:
- 主存储器:地址和存储的内容
- 算术逻辑单元 / 处理单元:执行信息的实际处理
- 程序控制单元 / 控制单元:指挥信息的处理
- 输入设备:将信息送入计算机中
- 输出设备:将处理结果以某种形式显示在计算机外

CPU 性能
- Instructions per cycle (IPC)
- Cycles per instruction (CPI)
- Instructions per second (IPS)
- 每秒百万指令 (MIPS)
计算机的顶层视图
W 3
Y 1
计算机的功能视图

计算机的顶层视图

计算机体系结构遇到的问题及解决方案
- CPU 的频率不能无限提高 → 改进 CPU 芯片结构
- 内存墙的存在 → 采用高速缓存
- CPU 等待 I/O 传输数据 → 采用中断机制
- 兼顾存储容量、速度和成本 → 层次式存储结构
- I/O 设备传输速率差异大 → 采用缓冲区和改进 I/O 操作技术
- 计算机部件互连复杂 → 采用总线
数据的机器级表示
W 9
Y 2
- 信息的二进制编码
- 整数的二进制表示
- 补码表示的优势,表示方法,真值计算
- 不同的整数二进制表示
- 浮点数的二进制表示
- 浮点数表示方法,规格化数,非规格化数,IEEE 754 标准
- 二进制编码的十进制数表示
- NBCD 码表示方法
编码
用少量简单的基本符号对复杂多样的信息进行一定规律的组合

整数的二进制表示
- 无符号整数
- 有符号整数
- 原码:符号位 + 数值位
- 反码:负数直接各位求反
- 移码:真值 + 偏移量
- 主要用于表示浮点数的指数
- 补码
浮点数的二进制表示
IEEE 754

二进制编码的十进制数表示
自然 BCD 码
NBCD 码
8421 码
- 0 ~ 9 → 0000 ~ 1001
- 符号:使用四个最高有效位
- 正 → 1100
- 负 → 1101
Transformer
- intToBinary
- binaryToInt
- decimalToNBCD
- NBCDToDecimal
- floatToBinary
- binaryToFloat
主要讲一讲 floatToBinary
- 第一步,对无穷大进行判断,并取绝对值:
public String floatToBinary(String floatStr) { Float num = Float.parseFloat(floatStr); if (num > Float.MAX_VALUE) return "+Inf"; else if (num < -Float.MAX_VALUE) return "-Inf"; else { StringBuilder builder = new StringBuilder(); if (num < 0) { builder.append("1"); num = -num; } else { builder.append("0"); }- 第二步,处理非规格化数:
if (num < Float.MIN_NORMAL) { // 非规格化数 builder.append("00000000"); for (int i = 0; i < 149; ++i) { num *= 2; } int frac = Math.round(num); for (int i = 22; i >= 0; --i) { if (Math.pow(2, i) <= frac) { builder.append("1"); frac -= Math.pow(2, i); } else { builder.append("0"); } } return builder.toString();由于非规格化数的最大值为
所以我们安全的将浮点数真值乘上 ,其最大值仅为 ,且必为整数
接着我们将这个整数转换为二进制,即得 frac 部分
- 第三步,处理规格化数:
} else { // 规格化数 int exp = 0; for (int i = 127; i >= -126; --i) { if (num >= Math.pow(2, i)) { exp = i; break; } }
num = num / (float) Math.pow(2, exp) - 1;
for (int i = 7; i >= 0; --i) { if (Math.pow(2, i) <= exp + 127) { builder.append("1"); exp -= Math.pow(2, i); } else { builder.append("0"); } }
for (int i = 0; i < 23; ++i) { num *= 2; }
long frac = Math.round(num); for (int i = 22; i >= 0; --i) { if (Math.pow(2, i) <= frac) { builder.append("1"); frac -= Math.pow(2, i); } else { builder.append("0"); } } return builder.toString(); } } }由于规格化数的范围为
我们首先需要提取 exp 和 frac 部分,即将浮点数真值转化为 的形式
此时的 ,需要加上偏置常数 127
而此时的 ,我们需要乘上 ,使其化为一个整数,再转换为二进制即可
数据校验码
W 5
Y 2
- 纠错
- 数据出错的原因,纠错的原理和处理过程
- 常用的数据校验码
- 奇偶校验码
- 海明码
- 循环冗余校验码
纠错

注意图中的符号有略微不同:
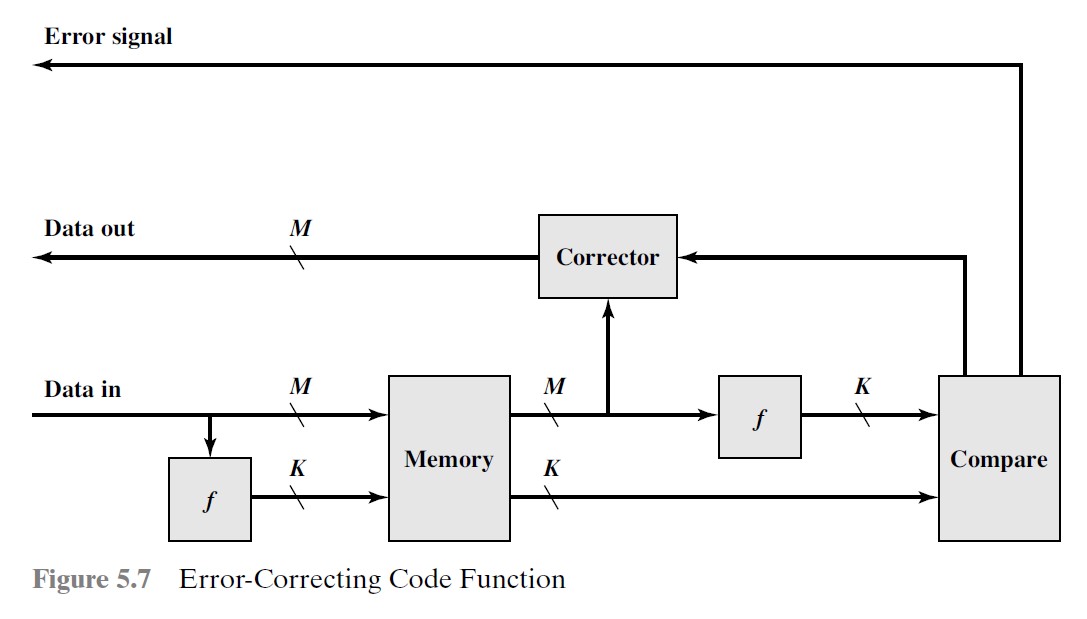
奇偶校验码
- 奇校验
- 0 → 奇数个 1
- 偶校验
- 0 → 偶数个 1
海明码
- 思想:二分查找,缩小范围
- 实现:异或操作
数据位 和校验位 的关系:
拓展:SEC-DED
Single-error correction, double-error detection
循环冗余校验
奇偶校验 → 将数据分为字节
循环冗余校验 → 流格式的数据
模 2 除法
1111000 对除数 1101 做模 2 除法:
1 0 1 1 // 商---------------1 1 1 1 0 0 0 // 被除数1 1 0 1 // 被除数首位为 1,上除数 1101--------------- 0 1 0 0 // 按位异或 0 0 0 0 // 被除数首位为 0,上 0000--------------- 1 0 0 0 // 按位异或 1 1 0 1 // 被除数首位为 1,上除数 1101--------------- 1 0 1 0 // 按位异或 1 1 0 1 // 被除数首位为 1,上除数 1101--------------- 1 1 1 // 按位异或,得到余数请与算术除法区分
编程实现
public static char[] Calculate(char[] data, String polynomial) { String trans = ""; for (int i = 0; i < data.length; ++i) { trans += data[i]; }
for (int i = 0; i < polynomial.length() - 1; ++i) { trans += "0"; } int[] tmp = new int[polynomial.length()]; for (int i = polynomial.length() - 1; i < trans.length(); ++i) { if (i == polynomial.length() - 1) { String sub = trans.substring(0, i + 1); assert sub.startsWith("1"); for (int j = 1; j < polynomial.length(); ++j) { tmp[j] = sub.charAt(j) - '0' ^ polynomial.charAt(j) - '0'; } } else { String sub = ""; for (int j = 1; j < tmp.length; ++j) { sub += tmp[j]; } sub += trans.charAt(i); if (sub.startsWith("1")) { for (int j = 1; j < polynomial.length(); ++j) { tmp[j] = sub.charAt(j) - '0' ^ polynomial.charAt(j) - '0'; } } else { for (int j = 1; j < polynomial.length(); ++j) { tmp[j] = sub.charAt(j) - '0' ^ 0; } } } }
String res = ""; for (int i = 1; i < tmp.length; ++i) { res += tmp[i]; } return res.toCharArray(); }基本思想是使用 tmp 数组存放中间 polynomial 长度的运算结果
整数运算
W 9
Y 3
- 算术逻辑单元 (ALU)
- 全加器
- 串行进位加法器,全先行进位加法器,部分先行进位加法器
- 补码表示的整数运算
- 加法
- 减法
- 乘法:布斯算法
- 除法
全加器
注意这里加法代表按位或,乘法代表按位与
拓展:半加器

使用半加器实现全加器:

请自行验证等价性
设:
- 与门延迟 → 1 ty
- 或门延迟 → 1 ty
- 异或门延迟 → 3 ty
则:
- 进位的延迟为 2 ty(朴素的实现,而非使用半加器的实现)
- 结果的延迟为 6 ty
串行进位加法器

沿用上述的延迟,有:
- 的延迟为
- 的延迟为
全先行进位加法器
由
记
则
将所有的 展开即可

沿用上述的延迟,有:
- 的延迟为
- 计算 和 → 1ty
- 计算 → 2ty
- 的延迟为
- 在计算 的同时计算
- 再计算 → 3ty
部分先行进位加法器
模块内先行进位,模块间串行进位

沿用上述的延迟,有:
- 计算所有的 和 → 1ty
- 的延迟为
- 的延迟为
- 的延迟为
- 的延迟为
- 的延迟最大为
拓展:延迟优化
成功说服 rtw 使其加入下一届课件
我们的想法是让块间的进位信号也能快速传递
由上述推导可知 ,其中:
类似的有 ,其中:
于是我们可以使用 和 ,在电路复杂性和延迟之间进行进一步优化

沿用上述的延迟,有:
- 和 的延迟为
- 的延迟为 或
- 为
- 其余为
- 的延迟为
- 计算 → 3ty
加法与减法
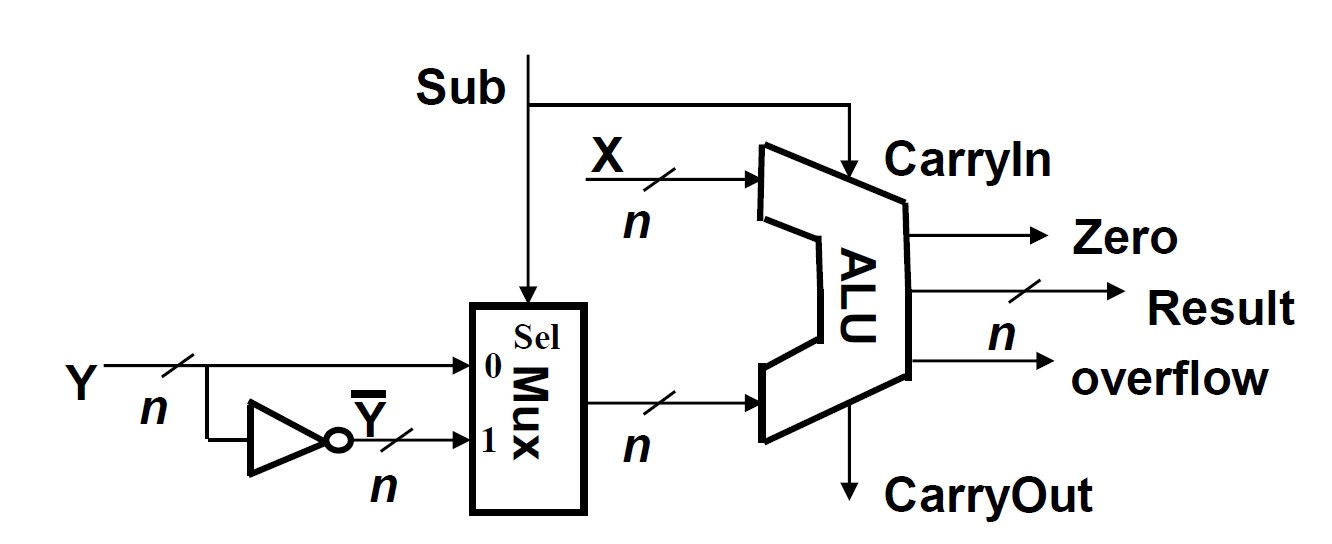
一些标志信息:
| ZF | SF | CF | OF | |
|---|---|---|---|---|
| 有符号运算 | 是否为零 | 最高位符号位 | 无意义 | |
| 无符号运算 | 是否为零 | 无意义 | 无意义 |
注意减法是将减数按位取反,并置 (即 ) 为 1
这里的 即
乘法
无符号数
手工演算——硬件优化

初始置全
有符号数
布斯算法

注意 多了一位
右移时为算术右移
除法
无符号数
手工演算——硬件优化

余数 寄存器和 余数 / 商 寄存器初始置被除数的扩展(有符号数,符号扩展;无符号数,零扩展)
有符号数
关于补码除法的余数:
- 余数与被除数同号
- 余数的绝对值尽量小
- 恢复余数
如果余数和除数的符号相同,做减法;如果余数和除数的符号不同,做加法
观察运算后余数是否变号,来判断够不够减
运算后,如果除数和被除数不同号,则将商替换为其相反数
- 不恢复余数
==Talk is cheap. Show me the code. ——Linus Torvalds==
符号约定:
- 被除数
- 除数
- 余数
- 商
- 补码位数
示例算术为 ,使用 4 位补码表示:
X - 1001Y - 0011首先判断除数是否为 0,接下来置 和 为被除数的符号扩展:
R - 1111Q - 1001对应代码:
String destStr = dest.toString(); StringBuilder R = new StringBuilder(); for (int i = 31; i >= 0; --i) R.append(destStr.charAt(0)); // 符号扩展 StringBuilder Q = new StringBuilder(destStr);第一步,需要判断除数和被除数符号是否相同,此处不相同:
sign(X) != sign(Y)
R = R + YR1 = 0010对应代码:
// initial if (src.toString().charAt(0) - '0' == dest.toString().charAt(0) - '0') { // 如果除数和被除数符号相同,则做减法;否则,做加法 DataType res = sub(src, new DataType(R.toString())); R = new StringBuilder(res.toString()); } else { DataType res = add(src, new DataType(R.toString())); R = new StringBuilder(res.toString()); }
boolean flag = R.toString().charAt(0) - '0' == src.toString().charAt(0) - '0';得到 ,并设置 flag 判断余数和除数符号是否相同
第二步,迭代 次,根据余数和除数符号进行运算:
---------| R | Q |---------
R1 = 0010sign(R1) == sign(Y) →┐ |0010 1001 |0101 0011 ←┤ // 左移,上商 1 |R2 = 2R1 - Y = 0010 ←┘sign(R2) == sign(Y)
0010 00110100 0111
R3 = 2R2 - Y = 0001sign(R3) == sign(Y)
0001 01110010 1111
R4 = 2R3 - Y = 1111sign(R4) != sign(Y)
1111 11111111 1111
R5 = 2R4 + Y = 0010sign(R5) == sign(Y) →┐ |0010 1110 | 1101 ←┘注意最后一次只需要左移 。
对应代码如下,请注意 flag 的更新和左移操作的位置:
if (flag) { // 如果余数和除数符号相同,则商𝑄𝑛=1;否则商𝑄𝑛=0 // 同时左移商和余数 R.append(Q.charAt(0)); R.deleteCharAt(0); Q.deleteCharAt(0); Q.append("1"); } else { R.append(Q.charAt(0)); R.deleteCharAt(0); Q.deleteCharAt(0); Q.append("0"); }
// iterate for (int i = 31; i >= 0; --i) { if (flag) { // 如果余数和除数符号相同,𝑅𝑖+1=2𝑅𝑖−𝑌;否则𝑅𝑖+1=2𝑅𝑖+𝑌 // 第一次循环,在之前已经移位了 DataType res = sub(src, new DataType(R.toString())); R = new StringBuilder(res.toString()); } else { DataType res = add(src, new DataType(R.toString())); R = new StringBuilder(res.toString()); }
// update flag flag = R.toString().charAt(0) - '0' == src.toString().charAt(0) - '0';
if (flag) { // 如果余数和除数符号相同,则商𝑄𝑛=1;否则商𝑄𝑛=0 // 同时左移商和余数 if (i != 0) { R.append(Q.charAt(0)); R.deleteCharAt(0); }
Q.deleteCharAt(0); Q.append("1"); } else { if (i != 0) { R.append(Q.charAt(0)); R.deleteCharAt(0); } Q.deleteCharAt(0); Q.append("0"); } }第三步,一些结果上的调整:
sign(X) != sign(Y)Q = 1101Q = Q + 1 = 1110
sign(X) != sign(R)sign(X) != sign(Y)R = 0010R = R - Y = 0010 + 1101 = 1111对应代码:
// final // 如果除数和被除数符号不同,商加 1 if (src.toString().charAt(0) - '0' != dest.toString().charAt(0) - '0') { DataType res = add(new DataType("00000000000000000000000000000001"), new DataType(Q.toString())); Q = new StringBuilder(res.toString()); }
// 若被除数和余数符号不同: // 若被除数和除数符号不同,余数减除数,反之加除数 if (R.toString().charAt(0) - '0' != dest.toString().charAt(0) - '0') { if (src.toString().charAt(0) - '0' != dest.toString().charAt(0) - '0') { DataType res = sub(src, new DataType(R.toString())); R = new StringBuilder(res.toString()); } else { DataType res = add(src, new DataType(R.toString())); R = new StringBuilder(res.toString()); } }
remainderReg = new DataType(R.toString());
// bug fix if (R.toString().equals(src.toString())) { // 若除数和余数相同,商加 1,余数置 0 remainderReg = new DataType("00000000000000000000000000000000"); DataType res = add(new DataType("00000000000000000000000000000001"), new DataType(Q.toString())); Q = new StringBuilder(res.toString()); } else if (sub(new DataType(src.toString()), new DataType("00000000000000000000000000000000")).toString().equals(R.toString())) { // 若除数的相反数和余数相同,商减 1,余数置 0 remainderReg = new DataType("00000000000000000000000000000000"); DataType res = sub(new DataType("00000000000000000000000000000001"), new DataType(Q.toString())); Q = new StringBuilder(res.toString()); }
return new DataType(Q.toString());Bug Fix:
浮点数运算
==Talk is cheap. Show me the code. ——Linus Torvalds==
W 9
Y 3
加法和减法
基本思想
- 将减法化归为加法
- 为了避免原码加法运算,需要填充一些位并转换为补码表示,计算后再将结果转换为原码表示
- 基于 GRS 保护位标准
实现
- 处理边界情况
// 处理边界情况 if (cornerCheck(addCorner, destStr, srcStr) != null) return new DataType(cornerCheck(addCorner, destStr, srcStr)); if (destStr.matches(IEEE754Float.NaN_Regular) || srcStr.matches(IEEE754Float.NaN_Regular)) return new DataType(IEEE754Float.NaN);- 提取符号、阶码、尾数
// 提取符号、阶码、尾数 String destSym = destStr.substring(0, 1); String srcSym = srcStr.substring(0, 1);
String destExp = destStr.substring(1, 9); String srcExp = srcStr.substring(1, 9);
String destFrac = destStr.substring(9); String srcFrac = srcStr.substring(9);
// 非规格化 → 规格化 if (destExp.equals("00000000")) { destExp = "00000001"; destFrac = "0".concat(destFrac).concat("000"); } else { destFrac = "1".concat(destFrac).concat("000"); }
if (srcExp.equals("00000000")) { srcExp = "00000001"; srcFrac = "0".concat(srcFrac).concat("000"); } else { srcFrac = "1".concat(srcFrac).concat("000"); }提取结束后尾数的位数应该等于 1 + 23 + 3 = 27。
- 对阶
采用小阶向大阶看齐的方式,小阶增加至大阶,同时尾数右移,保证对应真值不变:
// 对阶 int destExpNum = Integer.parseInt(transformer.binaryToInt(destExp)); int srcExpNum = Integer.parseInt(transformer.binaryToInt(srcExp)); int resExpNum; if (destExpNum <= srcExpNum) { destFrac = rightShift(destFrac, srcExpNum - destExpNum); resExpNum = srcExpNum; } else { srcFrac = rightShift(srcFrac, destExpNum - srcExpNum); resExpNum = destExpNum; }尾数右移时不能直接将最低位去掉,使用 rightShift 对尾数进行右移。
- 尾数相加或相减
if (destSym.equals("1")) { StringBuilder builder = new StringBuilder(); builder.append("1");
// padding builder.append("1"); builder.append("1"); builder.append("1"); builder.append("1");
int index = destFrac.lastIndexOf("1"); if (index != -1) { for (int i = 0; i < index; ++i) builder.append(destFrac.charAt(i) == '0' ? '1' : '0'); for (int i = index; i < destFrac.length(); ++i) builder.append(destFrac.charAt(i)); } else { for (int i = 0; i < destFrac.length(); ++i) builder.append(destFrac.charAt(i) == '0' ? '1' : '0'); } destFracSym = builder.toString(); } else { StringBuilder builder = new StringBuilder(); builder.append("0");
// padding builder.append("0"); builder.append("0"); builder.append("0"); builder.append("0");
for (int i = 0; i < destFrac.length(); ++i) builder.append(destFrac.charAt(i)); destFracSym = builder.toString(); }
...
resFracSym = alu.add(new DataType(srcFracSym), new DataType(destFracSym)).toString();
if (resFracSym.startsWith("1")) { resSymNum = 1; resFrac = resFracSym.substring(4); StringBuilder builder = new StringBuilder(); int index = resFrac.lastIndexOf("1"); if (index != -1) { for (int i = 0; i < index; ++i) builder.append(resFrac.charAt(i) == '0' ? '1' : '0'); for (int i = index; i < resFrac.length(); ++i) builder.append(resFrac.charAt(i)); } else { for (int i = 0; i < resFrac.length(); ++i) builder.append(resFrac.charAt(i) == '0' ? '1' : '0'); } resFrac = builder.toString(); } else { resSymNum = 0; resFrac = resFracSym.substring(4); }填充一些位至 32 位,并转换为补码表示,从而调用 alu 类的 add 方法,最后还要将结果转换为原码表示。
此时的 resFrac 有 28 位。
- 左规和右规
// 右规 if (resFrac.startsWith("1")) { if (resExpNum == 254) { return resSymNum == 0 ? new DataType(IEEE754Float.P_INF) : new DataType(IEEE754Float.N_INF); } else { resExpNum++; resFrac = rightShift(resFrac, 1); } }
// 左规 while (!resFrac.substring(1).startsWith("1")) { if (resExpNum > 1) { resFrac = alu.leftShift(resFrac, 1); resExpNum--; } else if (resExpNum == 1){ resExpNum--; break; } }
resFrac = resFrac.substring(1);右规:当运算后尾数大于 27 位时(检查 resFrac 最高位),此时应该将尾数右移 1 位并将阶码加 1
左规:当运算后尾数小于 27 位时(检查 resFrac 次高位,由于是规格化表示,次高位为 1 表示尾数为 27 位),此时应该不断将尾数左移并将阶码减少,直至尾数达到 27 位或阶码已经减为 0
最后别忘了去掉 resFrac 最高位。
- 舍入并返回
String res = round(resSymNum == 1 ? '1' : '0', transformer.intToBinary(String.valueOf(resExpNum)).substring(24), resFrac);
return new DataType(res);使用 round 进行舍入,传入的参数为 1 位符号位、8 位阶码、27 位尾数。
补充:原码加法
我们只考虑加法,因为容易发现减法是可以化归为加法的
- 两个操作数有相同的符号:直接相加
- 如果最高位有进位,则溢出
- 符号和第一个操作数相同
- 否则:加第二个操作数的补数
- 如果最高位有进位,正确,符号和第一个操作数相同
- 否则,计算它的补码,符号和第一个操作数相反
例子:
- 加法,最高位有进位,溢出
0.8125 + 0.625 = 1.4375
1101+ 1010------ 10111 ↓ 0111
0.4375- 减法,最高位有进位
0.8125 + (-0.625) = 0.1875
1101+ 0110------ 10011
0.1875- 减法,最高位无进位
0.625 + (-0.8125) = -0.1875
1010+ 0011------ 1101 ↓ 0011
-0.1875注意这里的符号只用于判断,不参与计算
乘法和除法
- 处理边界情况
类似加减法,略去。
- 提取符号、阶码、尾数
类似加减法,略去。
- 计算阶码
对于阶码的计算,与加减法运算不同的是,乘除法运算不再需要对阶操作,而是直接计算结果阶码。其计算过程分别为:
- 乘法:尾数相乘,阶码相加后减去偏置常数
- 除法:尾数相除,阶码相减后加上偏置常数
- 计算尾数并规格化
对于乘法而言,为 27 位无符号数乘法,返回 54 位结果:
// 27 位无符号数乘法 // 返回 54 位结果 private String multiply_27(String a, String b) { assert a.length() == 27 && b.length() == 27;
StringBuilder res = new StringBuilder(); for (int i = 0; i < 27; ++i) res.append("0"); for (int i = 0; i < 27; ++i) res.append(b.charAt(i));
StringBuilder temp = new StringBuilder(); for (int i = 0; i < 27; ++i) { if (res.charAt(53) == '1') { temp.delete(0, 27); temp.append(a); } else { temp.delete(0, 27); for (int j = 0; j < 27; ++j) temp.append("0"); }
int carry = 0; for (int j = 26; j >= 0; --j) { int p = res.charAt(j) - '0'; int q = temp.charAt(j) - '0'; int ans = p ^ q ^ carry; carry = (p & carry) | (q & carry) | (p & q); res.replace(j, j + 1, String.valueOf(ans)); }
res.deleteCharAt(53); res.insert(0, String.valueOf(carry)); }
return res.toString(); }其调用上下文如下:
// 尾数相乘 String resFrac = multiply_27(srcFrac, destFrac); // System.out.println(resFrac); resExpNum += 1;
// 尾数左移,阶码减 1 while (resFrac.charAt(0) == '0' && resExpNum > 0) { StringBuilder temp = new StringBuilder(resFrac); resFrac = temp.deleteCharAt(0).append(0).toString(); resExpNum--; }
// 尾数右移,阶码加 1 while (!resFrac.startsWith("000000000000000000000000000") && resExpNum < 0) { resFrac = rightShift(resFrac, 1); resExpNum++; }
if (resExpNum > 254) { // 阶码上溢 return new DataType(resSymNum == 0 ? IEEE754Float.P_INF : IEEE754Float.N_INF); } else if (resExpNum < 0) { // 阶码下溢 return new DataType(resSymNum == 0 ? IEEE754Float.P_ZERO : IEEE754Float.N_ZERO); } else if (resExpNum == 0) { // 尾数右移一次化为非规格化数 resFrac = rightShift(resFrac, 1); } else { // 此时阶码正常,无需任何操作 }由于乘积的隐藏位为 2 位,所以需要通过阶码加 1 的方式来保证尾数的隐藏位均为 1 位。
对于除法而言,为 27 位无符号数除法,要求被除数为 54 位,除数为 27 位,返回商的低 27 位:
// 27 位无符号数除法 // 要求被除数为 54 位,除数为 27 位 // 返回 27 位结果 public String divide_27(String a, String b) { assert a.length() == 54 && b.length() == 27; assert !b.equals("000000000000000000000000000");
// --- 54-bit --- --- 54-bit --- StringBuilder res = new StringBuilder(); for (int i = 0; i < 54; ++i) res.append(0); for (int i = 0; i < 54; ++i) res.append(a.charAt(i));
StringBuilder pos_b = new StringBuilder(); for (int i = 0; i < 27; ++i) pos_b.append(0); for (int i = 0; i < 27; ++i) pos_b.append(b.charAt(i));
StringBuilder neg_b = new StringBuilder(); int index = pos_b.lastIndexOf("1");
for (int i = 0; i < index; ++i) neg_b.append(pos_b.charAt(i) == '1' ? '0' : '1'); for (int i = index; i < 54; ++i) neg_b.append(pos_b.charAt(i));
for (int i = 0; i < 54; ++i) { if (compare_54(res.substring(0, 54), pos_b.toString())) { int carry = 0; for (int j = 53; j >= 0; --j) { int p = res.charAt(j) - '0'; int q = neg_b.charAt(j) - '0'; int ans = p ^ q ^ carry; carry = (p & carry) | (q & carry) | (p & q); res.replace(j, j + 1, String.valueOf(ans)); } res.deleteCharAt(0); res.append(1); } else { res.deleteCharAt(0); res.append(0); } }
StringBuilder ans = new StringBuilder(res.substring(54 + 27)); // 商的低 27 位
return ans.toString(); }关于位数的考量:
- 为了尽可能的保持运算的精度,我们刻意的将被除数左移了 27 位
- 假设被除数为 ,除数为 ,均为 27 位无符号数,有结果
- 然而一般的 27 位无符号数除法只能提供 的整数部分,而损失了小数部分的信息
- 为此,我们将 左移 27 位,此时有
- 相当于将结果的小数点右移了 27 位
- 举个例子,置 ,
- 一般的 27 位无符号数除法的结果为
- 优化精度的结果则为
- 而在浮点数尾数的上下文中,这恰好正是我们想要的结果
- 除法将 的偏移归一化了,而我们正好提前乘上了
- 所以这实际上是 54 位无符号数除法
- 由于此处的数据均为规格化数,首位为 ,可以保证余数和商可以通过 27 位表示
所以在调用上下文中需要将被除数末尾加上 27 个零:
destFrac += "000000000000000000000000000"; String resFrac = divide_27(destFrac, srcFrac); // System.out.println(resFrac);
if (resExpNum > 254) { return new DataType(resSymNum == 0 ? IEEE754Float.P_INF : IEEE754Float.N_INF); } else if (resExpNum < 0) { return new DataType(resSymNum == 0 ? IEEE754Float.P_ZERO : IEEE754Float.N_ZERO); } else if (resExpNum == 0) { // 尾数右移一次化为非规格化数 resFrac = rightShift(resFrac, 1); } else { // 此时阶码正常,无需任何操作 }目前只考虑规格化数的情况,所以可以省略左规和右规的步骤。
二进制编码的十进制数运算
- 加法
- 结果调整:进位引起加
0110 - 硬件实现
- 结果调整:进位引起加
- 减法
- 思路:参照补码进行数字反转,以避免借位
- 反转数字
- 结果调整
加法
两处观察:
- 当值落入 ,需要将值减去 ,并人为制造一个进位(或加上 ,自动生成一个进位)
- 当出现进位,需要将值加上
减法
需要对减数进行预处理:
0000 → 10010001 → 10000010 → 0111...1001 → 0000记该操作为反转
最后一位需要加 1,然后同加法运算之后,需要调整结果
- 如果有进位,舍弃进位
- 如果没有进位,对结果反转后加 1,并将结果符号设为负
编程实现
核心思想还是化归,我们只需处理如下两种情形:
- ,其中
- ,其中
内部存储器
W 5
Y 7
- 半导体存储器
- 读写存储器:RAM
- DRAM vs. SRAM
- DRAM → SDRAM, DDR
- 只读存储器:ROM, PROM
- 主要进行读操作的存储器:EPROM, EEPROM, flash memory
- 读写存储器:RAM
- 从位元到主存
- 位元 → 寻址单元 → 存储阵列 → 芯片 → 模块组织 → 主存
存储器
存储器由一定数量的单元构成,每个单元可以被唯一标识,每个单元都有存储一个数值的能力:
- 地址:单元的唯一标识符(采用二进制)
- 地址空间(寻址空间):可唯一标识的单元总数
- 寻址能力:存储在每个单元中的信息的位数
存储器层次结构

半导体存储器类型

RAM
- 快速读写
- 易失,需要维持供电

DRAM
在电容器上用电容充电的方式存储数据,电容器中有无电荷在分别代表二进制的 1 与 0
需要周期地充电刷新以维护数据存储
SRAM
使用传统触发器、逻辑门配置来存储二进制值
比较
DRAM 比相应的 SRAM 密度更高,价格更低,速度更慢
SRAM 一般用于高速缓存,DRAM 用于主存
高级的 DRAM 架构
SDRAM
Synchronous DRAM
SDRAM 与处理器的数据交互同步与外部的时钟信号,并且以处理器 / 存储器总线的最高速度运行,而不需要插入等待状态
DDR SDRAM
每个时钟周期发送两次数据,一次在时钟脉冲的上升沿,一次在下降沿
DDR → DDR2 → DDR3 → DDR4
增加操作频率
增加预取缓冲区
ROM
- 非易失
- 只读
PROM
芯片出厂时内容为全 0,只能写入一次,电写入
可擦除存储器
EPROM
光擦除,电写入
芯片级
EEPROM
电擦除,电写入
字节级
快闪存储器
电擦除,电写入
块级
比较
EPROM < 快闪 < EEPROM
价格和功能 ↑
从位元到主存
位元
半导体存储器的基本元件,用于存储 1 位数据
特性:
- 呈现两种稳态(或半稳态):分别表示二进制的 0 和 1
- 它们能够至少被写入数据一次:用来设置状态
- 它们能够被读取来获得状态信息
寻址单元
由若干相同地址的位元组成
寻址模式:
- 字节
- 字
存储阵列
由大量寻址单元组成
以 DRAM 为例:

寻址
地址译码器
减少地址引脚线:
- 行列复用
- 方阵
刷新
按行刷新
集中式刷新,Centralized refresh
- 停止读写操作,并刷新每一行
- 刷新时无法操作内存
分散式刷新,Decentralized refresh
- 在每个存储周期中,当读写操作完成时进行刷新
- 会增加每个存储周期的时间
异步刷新,Asynchronous refresh
- 每一行各自以 64ms 间隔刷新
- 效率高
芯片
以 DRAM 为例,其芯片引脚可能如下:

模块组织
- 位扩展:地址线不变,数据线增加
- 字扩展:地址线增加,数据线不变
- 字、位同时扩展:地址线增加,数据线增加
主存
使用插槽组合多个存储模块
Cache
W 4
Y 7
-
Cache 的目的、基本思路、工作流程
-
Cache 的若干问题
- 命中 vs. 未命中
- 未命中时将数据块传送到 Cache 中
- 平均访问时间
-
Cache 的设计要素
- Cache 容量
- 映射功能:直接映射,关联映射,组关联映射
- 替换算法:LRU,FIFO,LFU,随机
- 写策略:写直达,写回法
- 行大小
- Cache 数目:一级 vs. 多级,统一 vs. 分立
局部性原理
时间局部性
int factorial = 1;for (int i = 2; i <= n; i++) { factorial = factorial * i;}空间局部性
for (int i = 0; i < num; i++) { score[i] = final[i] * 0.4 + midterm[i] * 0.3 + assign[i] * 0.2 + activity[i] * 0.1;}平均访问时间
设命中率为
为访问 Cache 的时间
为访问主存的时间
则总时间为
可以推出,若 ,则
Cache 容量
容量 ↑
命中率 ↑
访问 Cache 的时间 ↑
映射功能
- 直接映射
- 简单,搜索代价小
- 容易抖动
- 适合大容量的 cache
- 关联映射
- 复杂,搜索代价大
- 不易抖动
- 适合小容量的 cache
- 组关联映射
- 折中

关联度
一个主存块映射到 cache 中可能存放的位置个数
- 直接映射:
- 关联映射:𝐶
- 组关联映射:𝐾
影响因素:
- 关联度越低,命中率越低
- 直接映射的命中率最低,关联映射的命中率最高
- 关联度越低,判断是否命中的时间越短
- 直接映射的命中时间最短,关联映射的命中时间最长
- 关联度越低,标记所占额外空间开销越小
- 直接映射的标记最短,关联映射的标记最长
替换算法
对于关联度 而言:
- 最近最少使用算法 (Least Recently Used, LRU)
- 先进先出算法 (First In First Out, FIFO)
- 最不经常使用算法 (Least Frequently Used, LFU)
- 随机替换算法 (Random)
写策略
主存和 cache 的一致性:当 cache 中的某个数据块被替换时,需要考虑该数据块是否被修改
- 写直达:所有写操作都同时对 cache 和主存进行
- 写回法:先更新 cache 中的数据,当 cache 中某个数据块被替换时,如果它被修改了,才被写回主存
行大小
行大小 ↑
- 前期:利用空间局部性,命中率提高
- 后期:容量固定的情况下,行数减少,命中率降低
Cache 数目
一级 vs. 多级
- 一级:减少处理器在外部总线上的活动
- 多级:减少处理器对总线上 DRAM 或 ROM 的访问
统一 vs. 分立
- 统一:更高的命中率,在获取指令和数据的负载之间自动进行平衡
- 分立:消除 cache 在流水线单元中的竞争(结构冒险)
编程实现
差点把 coa2021-programming08 搞没了,Git 是个危险的东西……
单独将 src 目录拷贝到一个新的文件夹中,在其中创建项目,初始化 Git,并创建 revised 分支书写标程的思路
基本内容
Cache 容量:
- 总大小 1MB
- 行大小 1KB
- 1024 个行
虚拟地址与 Cache 信息的互相转换:
- 虚拟地址 → Cache 信息
VA (32 位) = 标记和组号 (22 位) + 块内地址 (10 位)标记和组号即 blockNO
注意区分组号 (setNO) 和行号 (rowNO)
标记的占位长度为 位,若关联度为 ,则有效长度为
- Cache 信息 → 虚拟地址
考虑 1KB 对齐的情形,可以通过行号反推标记和组号,即 calculatePAddr 方法:
public String calculatePAddr(int rowNO) { // TODO
char[] tag = cache.get(rowNO).tag; int setLength = (int) (Math.log(SETS) / Math.log(2)); String setNOStr = transformer.intToBinary(String.valueOf(rowNO / setSize)).substring(32 - setLength); int tagLength = 22 - setLength; StringBuilder builder = new StringBuilder(); for (int i = 0; i < tagLength; ++i) builder.append(tag[i]); builder.append(setNOStr).append("0000000000"); return builder.toString(); }通过 rowNO / setSize 得到组号
映射策略
为简单期间,考虑 VA 为 1KB 对齐的情形,Cache 类的 read 和 write 函数都会通过 fetch 函数得到行号。并进行读写操作:
private int fetch(String pAddr) { // TODO
int blockNO = getBlockNO(pAddr); int rowNO = map(blockNO);
if (rowNO == -1) { rowNO = loadBlock(blockNO); }
assert rowNO != -1;
return rowNO; }fetch 函数将功能分解,首先取标记和组号,即 VA 的前 22 位,然后调用 map 方法:
private int map(int blockNO) { // TODO
int setNO = blockNO % SETS; char[] addrTag = calculateTag(blockNO); int st = setNO * setSize; int ed = (setNO + 1) * setSize; for (int rowNO = st; rowNO < ed; ++rowNO) { if (isTagMatch(rowNO, addrTag)) { replacementStrategy.hit(rowNO); return rowNO; } }
return -1; }map 方法根据具体的映射策略,取出 位的标记信息,并与 cache 中对应组的标记进行比对:
- 若命中,根据具体的替换策略更新 CacheLine 的信息
- 否则返回 -1,代表未命中
若未命中,fetch 方法调用 loadBlock 方法,传递标记和组号:
private int loadBlock(int blockNO) { // TODO
int setNO = blockNO % SETS; char[] addrTag = calculateTag(blockNO); int st = setNO * setSize; int ed = (setNO + 1) * setSize; char[] data = Memory.getMemory().read(transformer.intToBinary(String.valueOf(blockNO * LINE_SIZE_B)), LINE_SIZE_B);
if (SETS == 1024) { // 直接映射,无替换策略而言 int rowNO = setNO; update(rowNO, addrTag, data); return rowNO; } else { for (int rowNO = st; rowNO < ed; ++rowNO) { if (cache.get(rowNO).validBit == false) { update(rowNO, addrTag, data); return rowNO; } } return replacementStrategy.replace(st, ed, addrTag, data); } }这里需要注意根据标记和组号,得到数据在内存中的起始地址为 blockNO * LINE_SIZE_B
loadBlock 方法会根据具体的映射策略,进行 cache 的替换与更新:
- 关联度为 :直接替换
- 关联度 :先在组中找是否有无效的行,若没有再根据替换策略进行替换
public void update(int rowNO, char[] tag, char[] input) { // TODO
CacheLine line = cache.get(rowNO); line.update(tag, input); }update 方法将具体的更新信息转发给 CacheLine 内部类中:
private static class CacheLine {
...
void update(char[] tag, char[] data) { // TODO validBit = true;
visited = 1; timeStamp = System.currentTimeMillis();
System.arraycopy(tag, 0, this.tag, 0, tag.length); System.arraycopy(data, 0, this.data, 0, data.length); }
}需要注意对替换策略相关字段的初始化。
替换策略
- 最近最少使用算法 (Least Recently Used, LRU)
- 先进先出算法 (First In First Out, FIFO)
- 最不经常使用算法 (Least Frequently Used, LFU)
其中,LFU 通过 visited 字段标记最近的使用频数,而 LRU 通过 timeStamp 时间戳标记最近的使用时间,FIFO 也使用时间戳,不过其 hit 方法的实现中不需要更新时间戳。
写策略
主要修改 write 方法,测试用例只针对 FIFO 替换策略进行了测试。
- 写直达
// TODO if (isWriteBack) { cache.get(rowNO).dirty = true; } else { Memory.getMemory().write(calculatePAddr(rowNO), LINE_SIZE_B, cache_data); }需要调用上述介绍的 calculatePAddr 方法,写内存注意是 1KB 对齐
- 写回法
在更新 cache 之前,将 dirty 数据写回内存:
if (Cache.isWriteBack) { if (cache.isDirty(index) == true && cache.isValid(index) == true) { Memory.getMemory().write(cache.calculatePAddr(index), Cache.LINE_SIZE_B, cache.getData(index)); } }
cache.update(index, addrTag, input);需要判断有效性。
外部存储器
W 6
Y 8
-
磁盘存储器
- 软盘
- 硬盘:结构,读写机制,数据组织,格式化,I/O 访问时间,磁头寻道
-
光存储器
- CD, CD-ROM, CD-R, CD-RW
- DVD, DVD-R, DVD-RW
- Blu-ray
-
磁带
-
U 盘和固态硬盘
硬盘
材料
磁盘是由涂有可磁化材料的非磁性材料(基材)构成的圆形盘片
玻璃基材 → 支持磁头较低的飞行高度
结构

- 磁头
- 盘片:有上下两面
读写机制
在读或写操作期间,磁头静止,而盘片在其下方旋转
TODO
数据组织
- 磁道:从外到内编号 ↑
- 扇区:默认值为 512B

- 柱面:所有盘片上处于相同的相对位置的一组磁道

扇区划分
-
恒定角速度
- 磁盘能够以恒定的速度扫描信息
- 磁盘存储容量受到了最内层磁道所能实现的最大记录密度的限制
-
多带式记录
- 将盘面划分为多个同心圆区域,每个区域中各磁道的扇区数量是相同的,距离中心较远的分区包含的扇区数多于距离中心较近的分区
- 提升存储容量
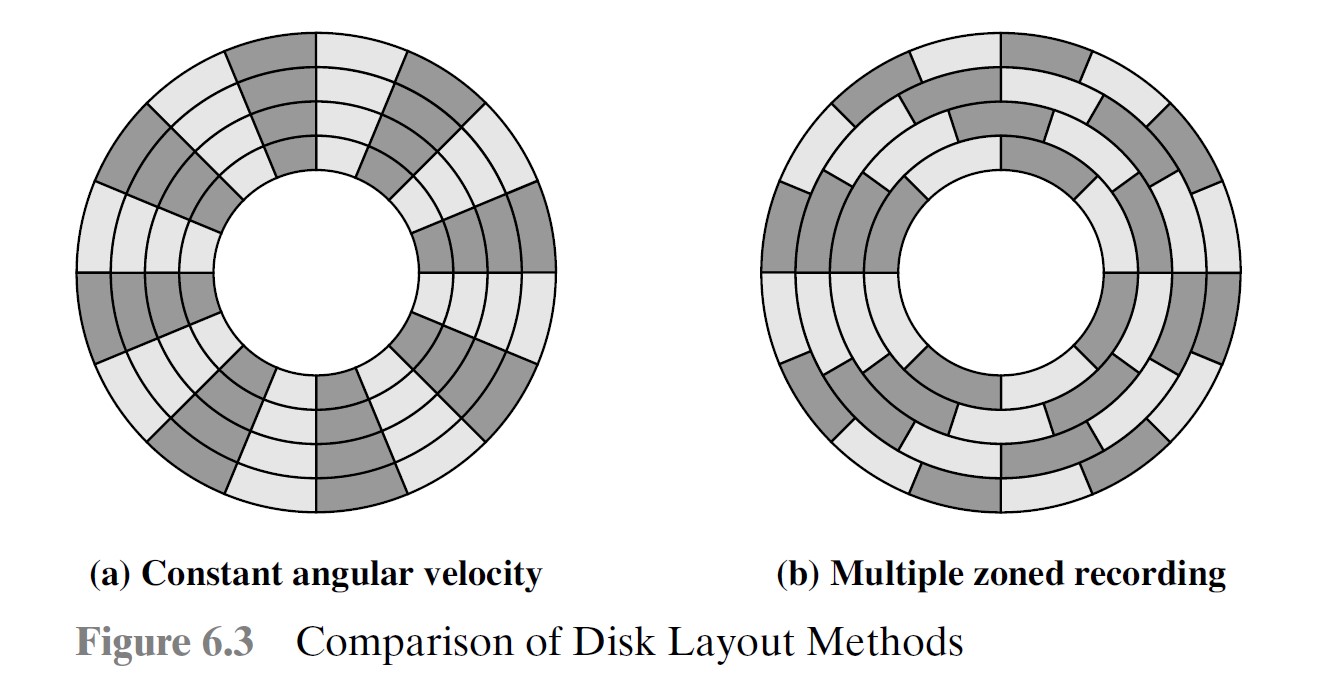
格式化
需要一些额外的控制数据,用来定位具体的扇区,并标注一些信息

I/O 访问时间
寻道时间:磁头定位到所需移动到的磁道所花费的时间,通常取平均时间
旋转延迟:等待响应扇区的起始处到达磁头所需的时间,通常取磁道旋转半周所需的时间
传送时间:数据传输所需的时间
则平均访问时间为:
其中:
- 为平均寻道时间
- 为待传送的字节数
- 为各磁道的字节数
- 为转速
磁头寻道
目标:当有多个访问磁盘任务时,使得平均寻道时间最小
-
先来先服务 (First Come First Service,FCFS)
-
最短寻道时间优先 (Shortest Seek Time First,SSTF)
可能产生饥饿现象,尤其是位于两端的磁道请求
- 扫描/电梯 (SCAN)
总是按照一个方向进行磁盘调度,直到该方向上的边缘,然后改变方向
- 循环扫描 (C-SCAN)
只有磁头朝某个方向移动时才会响应请求,移动到边缘后立即让磁头返回起点,返回途中不做任何处理
- LOOK
SCAN 算法的升级,只要磁头移动方向上不再有请求,就立即改变磁头的方向
- C-LOOK
C-SCAN 算法的改进,只要在磁头移动方向上不再有请求,就立即让磁头返回起点
光存储器

磁带
顺序读取
并行记录 vs. 串行记录(蛇形记录)
U 盘和固态硬盘
U 盘:采用了快闪存储器,属于非易失性半导体存储器
固态硬盘:与 U 盘没有本质区别:容量更大,存储性能更好
RAID
Redundant Arrays of Independent Disks
W 6
Y 8
基本思想:
- 将多个独立操作的磁盘按某种方式组织成磁盘阵列,以增加容量
- 将数据存储在多个盘体上,通过这些盘并行工作来提高数据传输率
- 采用数据冗余来进行错误恢复以提高系统可靠性
特性:
- 由一组物理磁盘驱动器组成,被视为单个的逻辑驱动器
- 数据是分布在多个物理磁盘上
- 冗余磁盘容量用于存储校验信息,保证磁盘万一损坏时能恢复数据

RAID 0
条带化,非冗余:
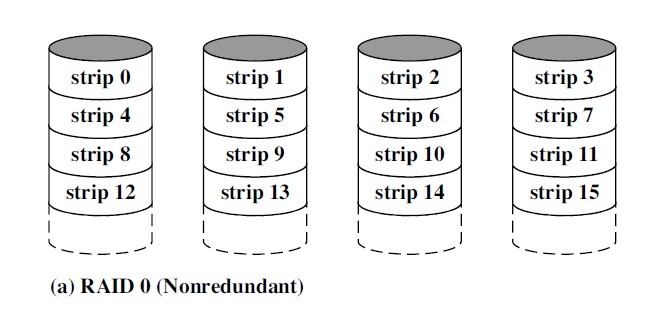
与单个大容量磁盘相比:
- 高数据传输率:请求大量逻辑相邻的数据,通过条带化让多个物理盘并行读写
- 高速响应 I/O 请求:两个 I/O 请求所需要的数据块可能在不同的磁盘上
- 数据可用性降低
RAID 1
条带化,备份所有数据:

与单个大容量磁盘相比:
- 高速响应 I/O 请求:即便是同一个磁盘上的数据块,也可以由两组硬盘分别响应
- 读请求可以由包含请求数据的两个对应磁盘中的某一个提供服务,可以选择寻道时间较小的那个
- 写请求需要更新两个对应的条带:可以并行完成,但受限于写入较慢的磁盘
- 单个磁盘损坏时不会影响数据访问,恢复受损磁盘简单
- 价格昂贵
RAID 01 vs. RAID 10
- RAID 01 = RAID 0 + 1
- 先做 RAID 0,再做 RAID 1
- RAID 10 = RAID 1 + 0
- 先做 RAID 1,再做 RAID 0
RAID 10 的数据可用性较高(先做冗余备份)
RAID 10 Vs RAID 01 (RAID 1+0 Vs RAID 0+1) Explained with Diagram
RAID 2
Deprecated
采用并行存取技术
希望所有磁盘都参与每个 I/O 请求的执行
条带非常小,经常只有一个字节或一个字

使用海明码纠错:
- 读取:获取请求的数据和对应的校验码
- 写入:所有数据盘和校验盘都被访问
适用于多磁盘易出错环境,对于单个磁盘和磁盘驱动器已经具备高可靠性的情况没有意义。
RAID 3
类似 RAID 2,使用奇偶校验码纠错:

当某一磁盘损坏时,可以用于重构数据。
这里已经明确定位到了出错的磁盘,所以奇偶校验码可以实现纠错的功能。
假设磁盘 出错,由:
两边异或 ,立得:
与单个大容量磁盘相比:
- 能够获得非常高的数据传输率,对于大量传送,性能改善特别明显
- 一次只能执行一个 I/O 请求,在面向多个 I/O 请求时,性能将受损
RAID 4
Deprecated
采用独立存取技术
每个磁盘成员的操作是独立的,各个 I/O 请求能够并行处理
采用相对较大的数据条带
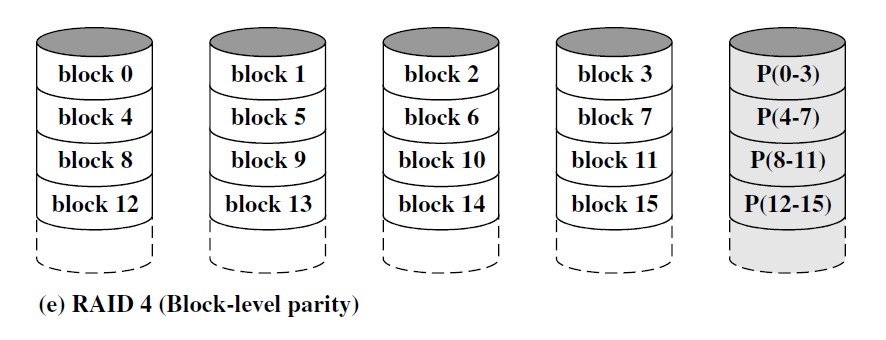
与单个大容量磁盘相比:
- 当执行较小规模的 I/O 写请求时,RAID 4 会遭遇写损失,对于每一次写操作,阵列管理软件不仅要修改用户数据,而且要修改相应的校验位
-
当涉及所有磁盘的数据条带的较大 I/O 写操作时,只要用新的数据位来进行简单的计算即可得到奇偶校验位
-
每一次写操作必须涉及到唯一的校验盘,校验盘会成为瓶颈(冲突,校验位在同一个物理盘上)
RAID 5
类似 RAID 4,将校验盘分解到每个物理盘上:

若修改 block 0,第一行会受影响,校验位所在的列也会受影响。
访问时的两读两写:
最好情形:两读并行,两写并行
最坏情形:无并行
RAID 50
先做 RAID 5,再做 RAID 0
RAID 6
采用两种不同的校验码,并将校验码以分开的块存于不同的磁盘中:

- 提升数据可用性
- 每次写都要影响两个校验块
虚拟存储器
W 8
Y 7
- 存储器管理
- 交换技术
- 分区
- 分页
- 虚拟存储器
- 分页式虚拟存储器
- 页表,虚拟地址和物理地址的转换
- CPU 访存过程
- TLB、页表、Cache 的缺失组合
- 分段式虚拟存储器
- 段页式虚拟存储器
- 分页式虚拟存储器
存储器管理
在多道程序系统中,主存需要进一步划分给多个任务,划分的任务由操作系统动态执行。
如何将更多任务装入主存:
- 增大主存容量
- 使用交换技术
- 当主存中没有处于就绪的任务时,操作系统调入其他任务来执行
- 分区和分页
- 虚拟存储器
- 请求分页:每次访问仅将当前需要的页面调入主存,而其他不活跃的页面放在外存磁盘上
- 虚拟地址
分区
分区方式将主存分为两大区域
- 系统区:固定的地址范围内,存放操作系统
- 用户区:存放所有用户程序
分区方式有如下两种
- 简单固定分区:空间浪费
- 可变长分区:空间碎片
分页
把主存分成固定长且比较小的存储块,称为页框(物理地址),每个任务也被划分成固定长的程序块,称为页(逻辑地址)
将页装入页框中,且无需采用连续的页框来存放一个任务中所有的页
虚拟存储器
请求分页,仅将当前需要的的页面调入主存
通过硬件(页表)将逻辑地址转换为物理地址,未命中时在主存和硬盘之间交换信息
设计的一些问题
以分页为例,指内存
类似 Cache 和主存之间,由于主存和硬盘之间更大的速度鸿沟,考量下述设计要素:
- 页大小
- 4 KB
- 内存容量较大
- 映射算法
- 全相联映射
- 提高命中率
- 写策略
- 写回
- 减少写硬盘的次数
分页式虚拟存储器
主存储器和虚拟地址空间都被划分为大小相等的页面:
- 虚拟页:虚拟地址空间中的页面
- 物理页:主存空间中的页面
页表
- 页表中包含了所有虚拟页的信息,包括虚拟页的存放位置、装入位、修改位、存取权限位等等
- 保存在主存中

存放位置信息:
- 未分配:
PTE 0 / 5 - 已缓存:
PTE 1 / 2 / 4 / 7 - 未缓存:
PTE 3 / 6
一些细节:
- 存放位置的长度固定,无论是未分配、已缓存还是未缓存
- 不需要在页表中记录虚页号,因为页表记录了所有虚拟页的信息
地址转换:
虚拟页号 + 页内偏移量 → 物理页号 + 页内偏移量
VA → PA
TLB
Translation Lookaside Buffer
页表的使用增加了主存的访问次数,为了减少访存次数,把页表中最活跃的几个页表项复制到高速缓存中:
- 映射:关联映射,组关联映射
- 替换:随机替换
CPU 访存过程

TLB、页表、Cache 的缺失组合

替换掉的不在主存中的页,TLE 和 Cache 中一定不会有相应有效的项
访存次数分析:
- 1 → 0
- 2 → 1
- 3 → 1
- 4 → 2
- 5 → 2 + 1 次硬盘
分段式虚拟存储器
将程序和数据分成不同长度的段,将所需的段加载到主存中
虚拟地址:段号 + 段内偏移量
优点:段的分界与程序的自然分界相对应,易于编译、管理、修改和保护
缺点:段的长度不固定
段页式虚拟存储器
将程序和数据分段,段内再进行分页,每个分段都有一个页表
虚拟地址:段号 + 页号 + 页内偏移量
优点:程序按段实现共享与保护
缺点:需要多次查表
编程实现
RTFM:
- INTEL 80386 PROGRAMMER’S REFERENCE MANUAL 1986
- Chapter 5 Memory Management
预备知识
- 逻辑地址:48 位
- 线性地址:32 位
- 物理地址:32 位
| Segment = true | Segment = false | |
|---|---|---|
| Page = true | 段页式 | 不存在 |
| Page = false | 分段式 | 实模式 |
段选择符
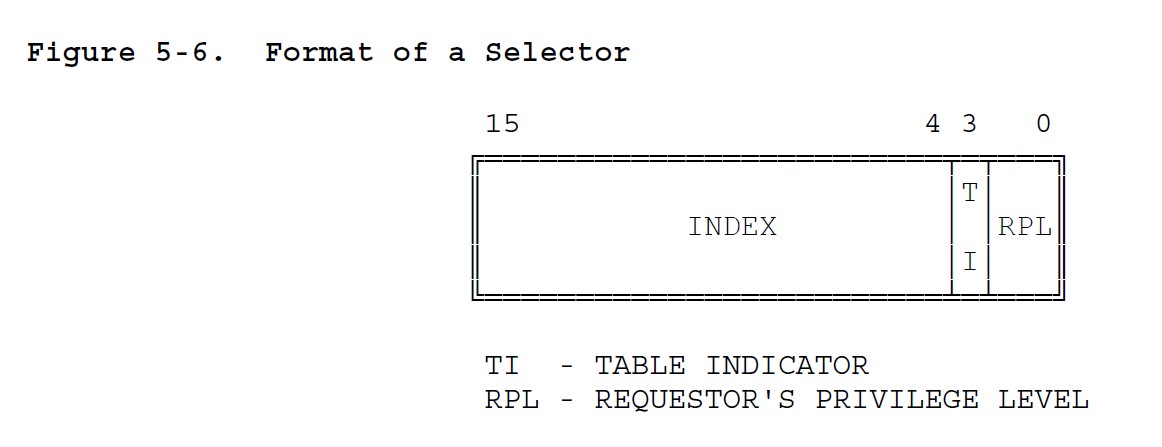
高 13 位的索引值用来确定当前使用的段描述符在段描述符表中的位置,表示是其中的第几个段表项。
段寄存器

段选择符存放在段寄存器中。
不过在编程作业中我们并不关心这一点……
段描述符

段描述符是一种数据结构,实际上就是分段方式下的段表项。
一个段描述符占用 8 个字节,下面是一些字段的含义:
- BASE:
Defines the location of the segment within the 4 gigabyte linear address space. The processor concatenates the three fragments of the base address to form a single 32-bit value.
- LIMIT:
Defines the size of the segment. When the processor concatenates the two parts of the limit field, a 20-bit value results. The processor interprets the limit field in one of two ways, depending on the setting of the granularity bit:
-
In units of one byte, to define a limit of up to 1 megabyte.
-
In units of 4 Kilobytes, to define a limit of up to 4 gigabytes. The limit is shifted left by 12 bits when loaded, and low-order one-bits are inserted.
- Granularity bit:
Specifies the units with which the LIMIT field is interpreted. When thebit is clear, the limit is interpreted in units of one byte; when set, the limit is interpreted in units of 4 Kilobytes.
其模拟如下:
private static class SegDescriptor { private char[] base = new char[32]; private char[] limit = new char[20]; private boolean validBit = false; private boolean granularity = false; }段描述符表
段描述符表实际上就是分段方式下的段表,由若干个段描述符组成:
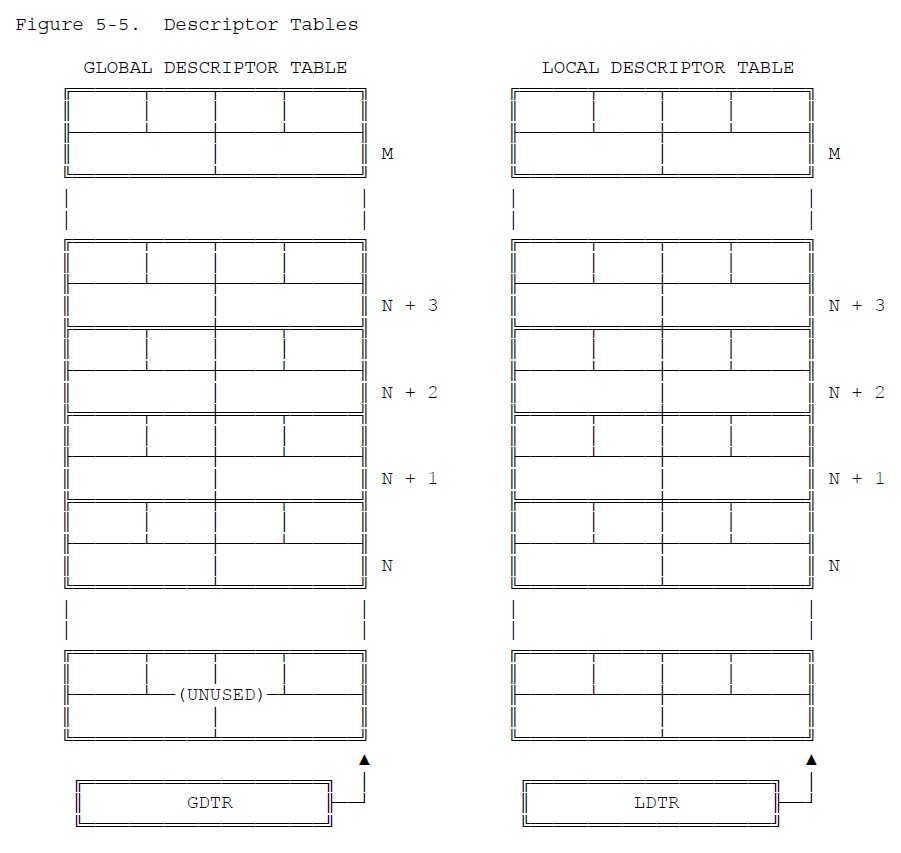
- 全局描述符表 (GDT)
- 局部描述符表 (LDT)
- ……
目前只考虑 GDT,其模拟如下:
private SegDescriptor[] GDT = new SegDescriptor[8 * 1024];页表
页表项模拟如下:
private static class PageItem { private char[] pageFrame; private boolean isInMem = false; }页表模拟如下:
private final PageItem[] pageTbl = new PageItem[Disk.DISK_SIZE_B / Memory.PAGE_SIZE_B];注意页表中包含了所有虚拟页的信息,而我们认为虚拟地址空间的大小为磁盘的大小,所以页表项的个数为Disk.DISK_SIZE_B / Memory.PAGE_SIZE_B
TLB
- 256 行
- 全相联映射
- FIFO 替换策略
TLB 项模拟如下:
private static class TLBLine { boolean valid = false; int vPageNo; char[] pageFrame = new char[20]; Long timeStamp = 0L; }注意 TLB 项在 TLB 中的下标与 vPageNo 不一致,不要和页表项混淆了。
timeStamp 用于 FIFO,所以 TLB hit 不必更新时间戳。
地址转换概述
逻辑地址 → 线性地址
15 0 31 0 LOGICAL +----------------+ +-------------------------------------+ ADDRESS | SELECTOR | | OFFSET | +---+---------+--+ +-------------------+-----------------+ +------+ V | | DESCRIPTOR TABLE | | +------------+ | | | | | | | | | | | | | | | | | | |------------| | | | SEGMENT | BASE +---+ | +->| DESCRIPTOR |-------------->| + |<------+ |------------| ADDRESS +-+-+ | | | +------------+ | V LINEAR +------------+-----------+--------------+ ADDRESS | DIR | PAGE | OFFSET | +------------+-----------+--------------+48 位的逻辑地址包含 16 位的段选择符和 32 位的段内偏移量。
MMU 首先通过段选择符内的 13 位索引值,从段描述符表中找到对应的段描述符,从中取出 32 位的基地址,与逻辑地址中 32 位的段内偏移量相加,就得到 32 位线性地址。
线性地址 → 物理地址
PAGE FRAME +-----------+-----------+----------+ +---------------+ | DIR | PAGE | OFFSET | | | +-----+-----+-----+-----+-----+----+ | | | | | | | +-------------+ | +------------->| PHYSICAL | | | | ADDRESS | | PAGE DIRECTORY | PAGE TABLE | | | +---------------+ | +---------------+ | | | | | | | | +---------------+ | | | | |---------------| ^ | | | +-->| PG TBL ENTRY |--------------+ | |---------------| |---------------| +->| DIR ENTRY |--+ | | |---------------| | | | | | | | | +---------------+ | +---------------+ ^ | ^+-------+ | +---------------+| CR3 |--------++-------+上图为 80386 的地址转换过程,在编程作业中简化为:
虚拟页号 + 页内偏移量 → 物理页号 + 页内偏移量
其中页号 20 位,页内偏移量 12 位。
实现
地址转换全貌
核心方法 addressTranslation:
private String addressTranslation(String logicAddr, int length) { String linearAddr; // 32 位线性地址 String physicalAddr; // 32 位物理地址 if (!Memory.SEGMENT) { // 实模式:线性地址等于物理地址 linearAddr = toRealLinearAddr(logicAddr); memory.real_load(linearAddr, length); // 从磁盘中加载到内存 physicalAddr = linearAddr; } else { // 分段模式 int segIndex = getSegIndex(logicAddr); if (!memory.isValidSegDes(segIndex)) { // 缺段中断,该段不在内存中,内存从磁盘加载该段索引的数据 memory.seg_load(segIndex); } linearAddr = toSegLinearAddr(logicAddr); // 权限检查 int start = Integer.parseInt(transformer.binaryToInt(linearAddr)); int base = chars2int(memory.getBaseOfSegDes(segIndex)); long limit = chars2int(memory.getLimitOfSegDes(segIndex)); if (memory.isGranularitySegDes(segIndex)) { limit = (limit + 1) * Memory.PAGE_SIZE_B - 1; } if ((start < base) || (start + length > base + limit)) { throw new SecurityException("Segmentation Fault"); } if (!Memory.PAGE) { // 分段模式:线性地址等于物理地址 physicalAddr = linearAddr; } else { // 段页式 int startvPageNo = Integer.parseInt(transformer.binaryToInt(linearAddr.substring(0, 20))); // 高 20 位表示虚拟页号 int offset = Integer.parseInt(transformer.binaryToInt(linearAddr.substring(20, 32))); // 低 12 位的页内偏移 int pages = (length - offset + Memory.PAGE_SIZE_B - 1) / Memory.PAGE_SIZE_B; if (offset > 0) pages++; int endvPageNo = startvPageNo + pages - 1; for (int i = startvPageNo; i <= endvPageNo; i++) { if (TLB.isAvailable) { if (tlb.getPageFrameFromTLB(i) == null) { // TLB 缺失 if (!memory.isValidPage(i)) { // TLB 缺失且缺页 memory.page_load(i); // 内存从磁盘加载该页的数据 tlb.write(i); // 填 TLB } else { // TLB 缺失但页表命中 tlb.write(i); // 填 TLB } } else { // do nothing } } else { if (!memory.isValidPage(i)) { // 缺页中断,该页不在内存中,内存从磁盘加载该页的数据 memory.page_load(i); } } } physicalAddr = toPagePhysicalAddr(linearAddr); } } return physicalAddr; }startvPageNo ~ endvPageNo 的遍历是考虑到地址访问跨页的情形。
下面我们需要实现三个地址转换和三个数据加载的方法。
实模式
逻辑地址通过如下变换:
物理地址 = 基址 << 4 + 偏移量转换为物理地址。
得到物理地址直接从磁盘中加载数据到内存。
实现略。
分段式
地址转换如下:
private String toSegLinearAddr(String logicAddr) { int segmentDescriptorIndex = Integer.valueOf(logicAddr.substring(0, 13), 2); int base = chars2int(memory.getBaseOfSegDes(segmentDescriptorIndex)); int offset = Integer.valueOf(logicAddr.substring(16), 2); int linearAddr = base + offset; String linearAddrStr = String.valueOf(linearAddr);
return transformer.intToBinary(linearAddrStr); }数据加载如下:
public void seg_load(int segIndex) { SegDescriptor sd = getSegDescriptor(segIndex); sd.base = "00000000000000000000000000000000".toCharArray(); sd.limit = "11111111111111111111".toCharArray(); sd.validBit = true; sd.granularity = PAGE; if (!PAGE) { String pAddr = String.valueOf(sd.base); int len = Integer.parseInt(transformer.binaryToInt(String.valueOf(sd.limit))); char[] data = disk.read(pAddr, len); write(pAddr, len, data); } }我们约定,每个由 MMU 装载进入 GDT 的段,其段基址均为全 0,其限长均为全 1,未开启分页时粒度为 false,开启分页后粒度为 true
在分段式中,我们会加载硬盘前 1048575 B ≈ 1 MB 的数据到内存。
在段页式下,此处无需加载数据,只需要填写 GDT。
Linux 操作系统为了使它能够移植到绝大多数流行的处理器平台,就是把所有段基址设为全 0 的、段限长设为全 1 的。但即使 Linux 操作系统这么做了,在进行地址转换的时候,它也是需要去查 GDT 的。可以说,查 GDT 是所有系统的必备步骤。因此,我们即使规定了段基址为全 0,我们也需要考察大家是否正确进行了查表操作。
段页式
地址转换如下:
private String toPagePhysicalAddr(String linearAddr) { String vPageNo = linearAddr.substring(0, 20); String offset = linearAddr.substring(20);
char[] page; if (TLB.isAvailable) { page = TLB.getTLB().getPageFrameFromTLB(Integer.valueOf(vPageNo, 2)); } else { page = memory.getFrameOfPage(Integer.valueOf(vPageNo, 2)); } assert page != null;
StringBuilder builder = new StringBuilder(String.valueOf(page)); builder.append(offset); assert builder.length() == 32;
return builder.toString(); }数据加载如下:
public void page_load(int vPageNo) { int pPageNo = -1; for (int i = 0; i < MEM_SIZE_B / PAGE_SIZE_B; ++i) { if (!pageValid[i]) { pPageNo = i; break; } } assert pPageNo >= 0;
PageItem page = getPageItem(vPageNo); page.isInMem = true; pageValid[pPageNo] = true; page.pageFrame = transformer.intToBinary(String.valueOf(pPageNo)).substring(12).toCharArray();
int unit = (int) Math.pow(2, 12); int base = vPageNo * unit; String baseAddr = transformer.intToBinary(String.valueOf(base));
char[] data = disk.read(baseAddr, unit);
StringBuilder builder = new StringBuilder(String.valueOf(page.pageFrame)); builder.append("000000000000"); assert builder.length() == 32;
write(builder.toString(), unit, data); }需要注意的是虚实之间的关系,考虑加载第 个虚页:
- 遍历整个物理页框(不是页表的虚拟地址空间,而是内存的物理地址空间)寻找空闲的物理页框 ,为简单起见,此处使用了
pageValid有效位数组 - 置第 个虚页对应页表项的物理页框号为 ,并设置页表项和物理页框的有效位
- 在内存偏移
y * PAGE_SIZE_B处写入数据,对应数据在磁盘中的偏移为x * PAGE_SIZE_B
再强调一遍,页表中包含了所有虚拟页的信息,物理页对应的是内存:
- pPageNo 为物理页号,范围:
0 ~ MEM_SIZE_B / PAGE_SIZE_B - vPageNo 为虚拟页号,范围:
0 ~ DISK_SIZE_B/ PAGE_SIZE_B
分页机制的基本思想其实就是,为每个进程都提供一个独立的、极大的虚拟地址空间,将主存里放不下的页放到磁盘上去。
在真实的计算机磁盘中,会有专门的地方来存放虚页:在 Windows 下是 pagefile.sys 文件,在 Linux 下是 swap 分区。
因此,无论是在实模式还是分段式还是段页式,当你访问磁盘的时候,请保证你用来访问磁盘的是线性地址。上面所说的用来加载段的时候用的段基址、加载页的时候用的虚页起始地址,都属于线性地址。
总线
W 3
Y 8
- 总线
- 概念,类型,结构
- 设计要素
- 用途:专用总线,复用总线
- 仲裁:集中式,分布式
- 时序:同步,异步,半同步,分离事务
- 带宽和数据传输速率
- 层次结构:单总线,双总线,多总线
总线概念
总线是连接两个或多个设备的通信通路
总线类型
- 芯片内部总线:连接芯片内部的各个部分
- 系统总线:连接 CPU、存储器、I/O 控制器和其他功能设备
- 通信总线:连接主机和 I/O 设备,或连接不同的计算机系统
我们主要研究系统总线
总线结构
- 数据线:数据线的数量决定了一次可以传输的数据的大小
- 地址线:地址线的数量决定了寻址空间的大小
- 控制线
总线上数据传输的特点
- 总线可以被多个设备监听,但同一时刻只能由一个设备发送数据
- 当总线在被使用过程中,其它设备不可以抢占
总线仲裁
当多个设备需要与总线通信时,通过某种策略选择一个设备
平衡因素:
- 优先级:优先级高的设备优先被服务
- 公平性:优先级最低的设备不能一直被延迟
集中式
由仲裁器或总线控制器负责分配总线使用权
链式查询

在总线不忙的前提上,各设备向总线仲裁器发起请求
总线仲裁器 → 设备 1 → 设备 2 → ...对电路故障敏感
限制总线的速度
计数器查询
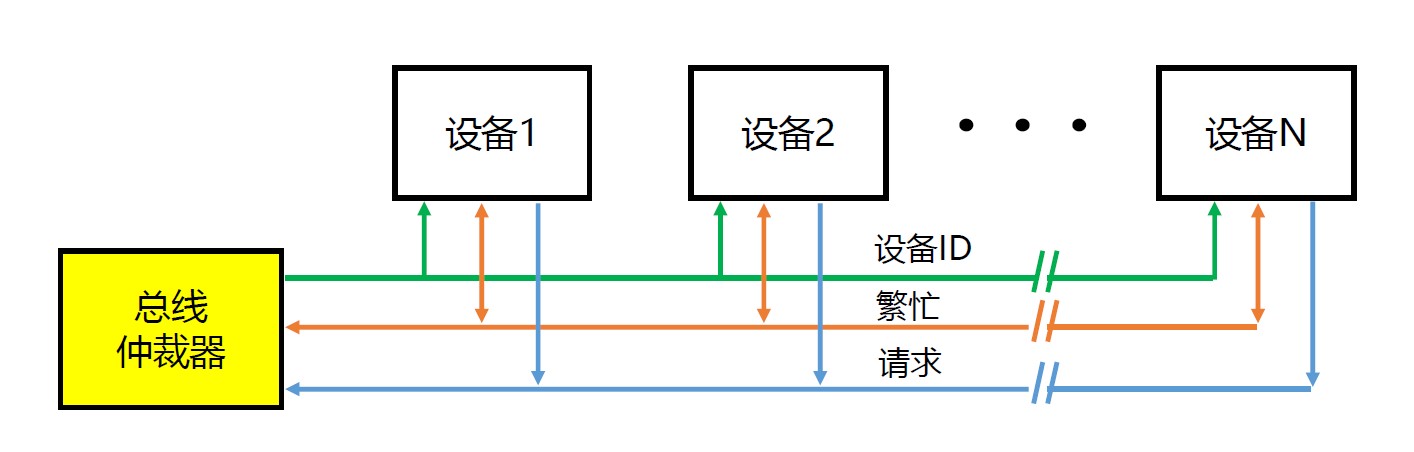
在总线不忙的前提上,各设备向总线仲裁器发起请求
总线仲裁器 → 设备 1总线仲裁器 → 设备 2...通过使用不同的初始计数,可以灵活地确定设备优先级
限制总线的速度
独立请求

在总线不忙的前提上,各设备向总线仲裁器独立发起请求
总线仲裁器决定(策略灵活)哪个设备可以使用总线
快速响应
分布式
每个设备都包含访问控制逻辑,各设备共同作用分享总线
自举式

优先级:
设备 3 > 设备 2 > 设备 1 > 设备 0- 设备 3 只关心总线是否忙,并通过 BR3 表达自己使用总线的意愿
- 设备 2 监听 BR3,并通过 BR2 表达自己使用总线的意愿
- 设备 1 监听 BR3 和 BR2,并通过 BR1 表达自己使用总线的意愿
- 设备 0 监听 BR3 和 BR2 和 BR1,无法表达自己使用总线的意愿
冲突检测
只要总线不忙,就去使用总线
若产生冲突,所有使用总线的设备停止数据传输,并分别在随机间隔时间后再次请求总线
时序
确定每个总线事务的开始和结束时间
总线事务:地址 + 数据 + … + 数据
同步时序
事件的发生由时钟决定
- 所有设备共享同一个时钟
- 总线长度受到时钟偏差的限制
- 总线不能太长,因为时钟也是一种信号
异步时序
一个事件的发生取决于前一个事件的发生
- 可以灵活地协调速度不同的设备
- 对噪声敏感
握手策略

Ready → 请求发起方,以 CPU 为例
Ack → 响应方,以 Memory 为例
非互锁:
- Ready ↑ → Ack ↑
- CPU 需要通知 Memory,Memory 才能读取数据
半互锁:
- Ready ↑ → Ack ↑
- CPU 需要通知 Memory,Memory 才能读取数据
- Ack ↑ → Ready ↓
- Memory 需要通知 CPU,Memory 可以被读取了
- 否则若 CPU 在 Memory 响应前撤去了信号,Memory 便会一直等待
全互锁:
- Ready ↑ → Ack ↑
- CPU 需要通知 Memory,Memory 才能读取数据
- Ack ↑ → Ready ↓
- Memory 需要通知 CPU,Memory 可以被读取了
- Ready ↓ → Ack ↓
- CPU 需要通知 Memory 请求结束,Memory 才能响应其他的请求
- 否则若 Memory 提前读取完撤去了信号,CPU 便会一直等待
异步数据传输
这里将地址线和数据线复用:
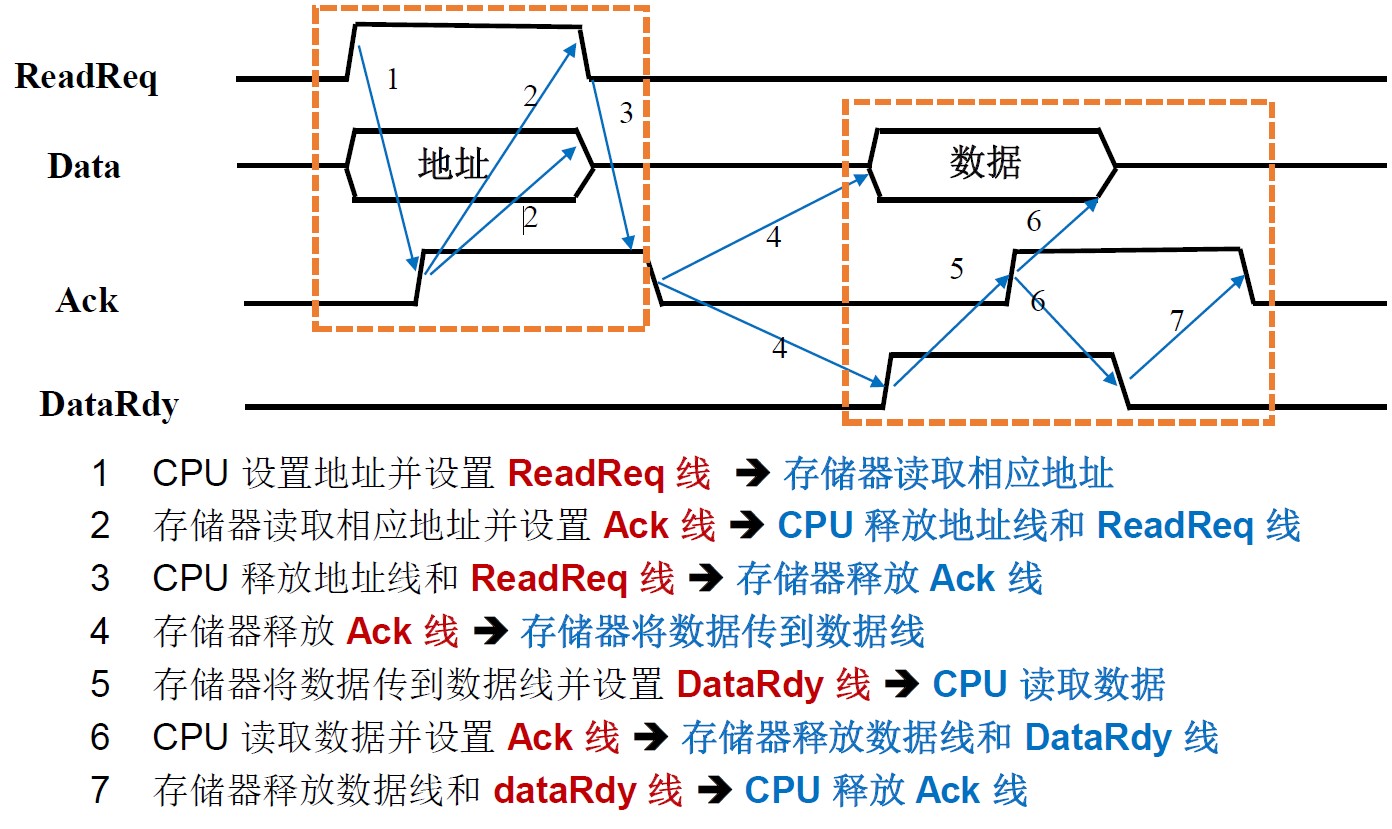
半同步
同步时序和异步时序相结合
准备和响应信号在时钟上升沿有效,从而减少了噪声的影响
分离事务
将一个总线事件分离为两个过程
设备准备数据期间释放总线
总线带宽和数据传输速率
- 总线带宽
- 总线的最大数据传输速率
- 不要考虑总线仲裁、地址传输等因素
- 数据传输速率
- 考虑地址传输、握手等因素
区分总线带宽与总线宽度
如何提高
- 提高时钟频率
- 增加数据总线宽度
- 每次传输更多的数据(成本:更多的总线线路)
- 块传输
- 传输一次地址就传输一块数据(成本:高复杂性)
- 分离总线事务
- 减少总线空闲时间(成本:复杂性高,增加每个事务的持续时间)
- 分离地址线和数据线
- 同时传输地址和数据(成本:更多的总线线路)
层次结构
单总线
一条系统总线
双总线
- 结构Ⅰ:在 CPU 和存储器中间增加一个存储器总线
- 结构Ⅱ:将系统总线分为存储器总线(不同于结构Ⅰ)、I/O 总线和 IOP (Input-Output Processor)
多总线
- 本地总线,连接 CPU 和 Cache
- DMA 总线,连接存储器和高速 I/O
- 高速 I/O 总线
指令系统
W 10 / 11
Y 4
- 指令
- 操作码
- 操作数
- 寻址方式:立即寻址,直接寻址,间接寻址,寄存器寻址,寄存器间接寻址,偏移寻址,栈寻址
- 指令格式:指令长度,位分配,变长指令
- 指令集设计
指令集
CPU 能执行的各种不同指令的集合
指令要素
- 操作码
- 源操作数引用
- 结果操作数引用
- 下一指令引用
操作码
- 数据传送
- 算术运算
- 逻辑运算
- 转换
- 输入输出
- 系统控制
- 控制转移
主要是控制转移指令:
- 分支 / 跳转指令:显式给出地址
- 跳步指令:包含一个隐含地址
- 过程调用指令:程序计数器的保存问题
- 使用寄存器:不允许嵌套调用
- 返回地址存于过程开始处:不允许递归调用,即对某个函数的调用只有同时存在一个,不可重入
- 使用栈
操作数
- 地址
- 数值
- 字符
- 逻辑数据
- 大端序和小端序
一个指令需要有 4 个地址引用:
- 两个源操作数
- 一个目的操作数
- 下一指令地址(通常是隐含的)

所以可以分为:
- 三地址指令
- 两地址指令
- 单地址指令:隐含累加器 AC
操作数引用
记号:
A: 指令中地址字段的内容R: 指向寄存器的指令字段的内容EA: 被访问未知的有效地址(X): 存储器位置 X 或者寄存器 X 的内容
寻址方式:
- 立即寻址
- 直接寻址:在当代计算机体系结构中不多见
- 间接寻址
- 寄存器寻址
- 寄存器间接寻址
- 偏移寻址
- 相对寻址:隐含引用的寄存器是程序计数器
- 基址寄存器寻址:
- 被引用的寄存器含有一个存储器地址
- 变址寻址:
- 与基址寄存器寻址的区别:存放基址的位置不同
- 后变址
- 间接寻址之后变址
- 前变址
- 变址之后间接寻址
- 栈寻址
一图胜千言:

指令格式
不是现在应该深究的内容
- 指令长度
- 位分配
- 变长指令
指令集设计
不是现在应该深究的内容
指令周期和指令流水线
W 12
Y 5 / 6
- 指令周期
- 取指周期、间址周期、执行周期、中断周期
- 数据流
- 流水线
- 两阶段,六阶段
- 流水线性能
- 冒险
- 结构冒险,数据冒险,控制冒险
指令周期
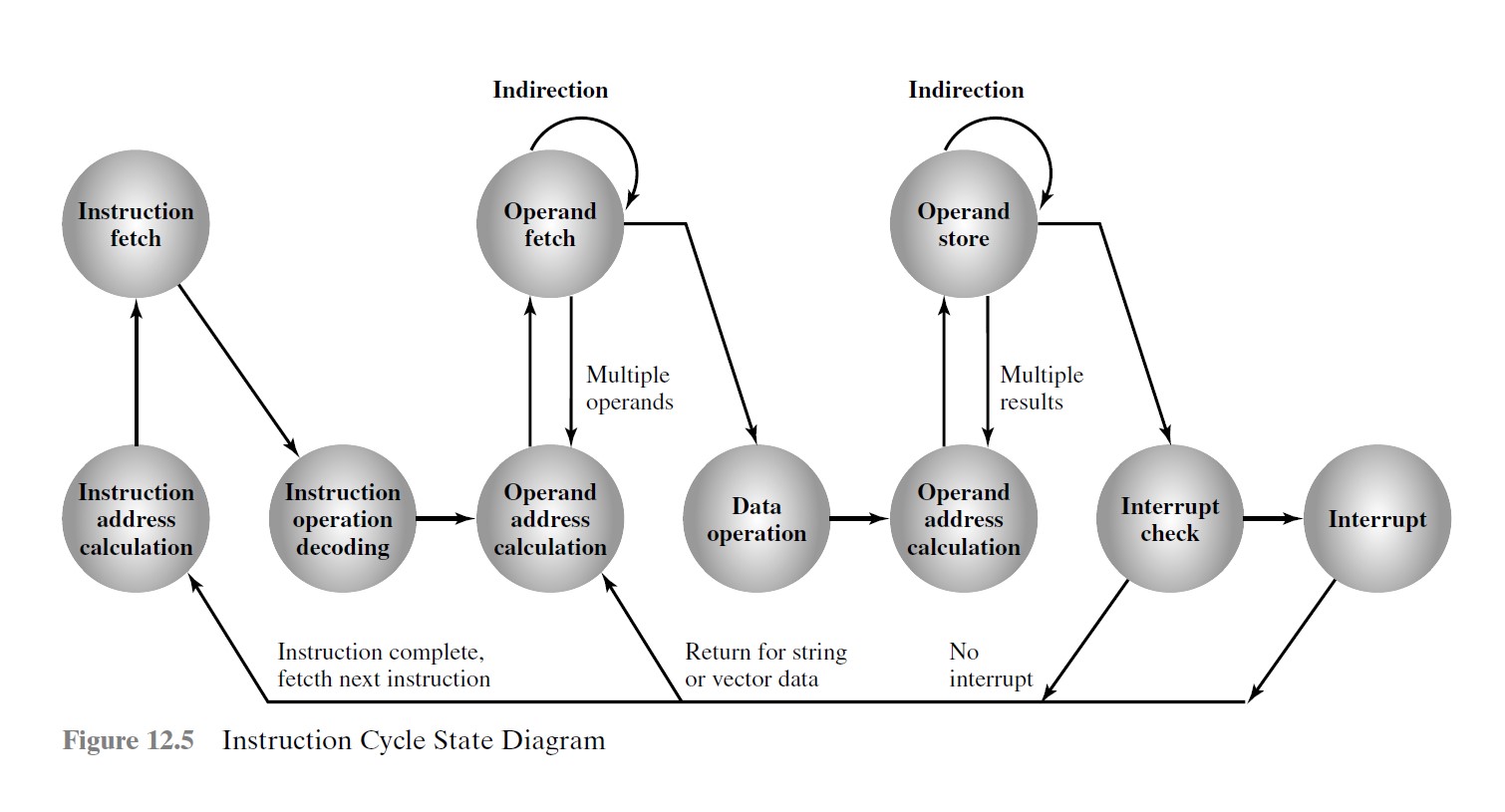
注意间接周期是取操作数的有效地址,而非操作数,操作数在执行阶段取
数据流
取指周期
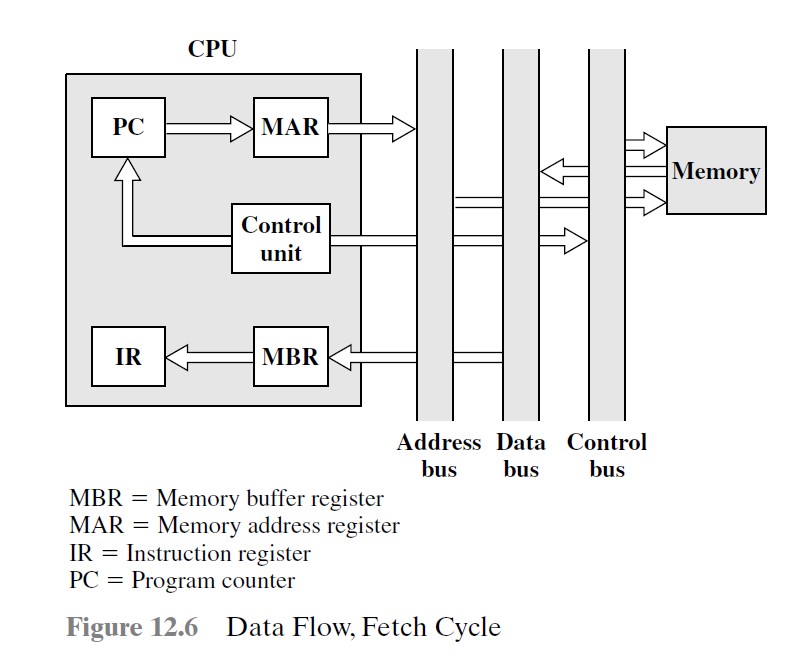
PC → MAR → 指令地址在地址总线
存储器读 → 指令数据在数据总线
指令数据 → MBR → IR
间接(间址)周期

控制器检查 IR 中是否有使用间接寻址的操作数
MBR → MAR → 操作数引用在地址总线
存储器读 → 操作数的有效地址在数据总线
中断周期
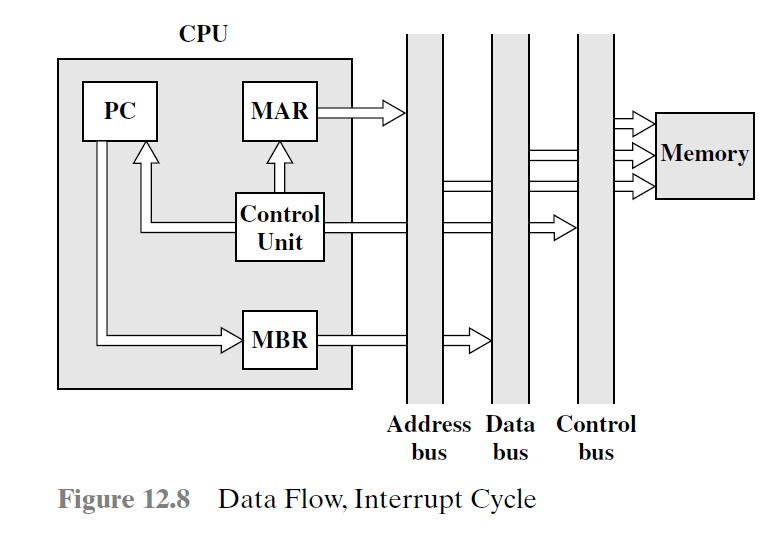
PC → MBR → 数据总线
一个存储器位置 → MAR → 地址总线
存储器写 → 保存 PC 在某个位置
中断子程序的地址 → PC
流水线
两阶段
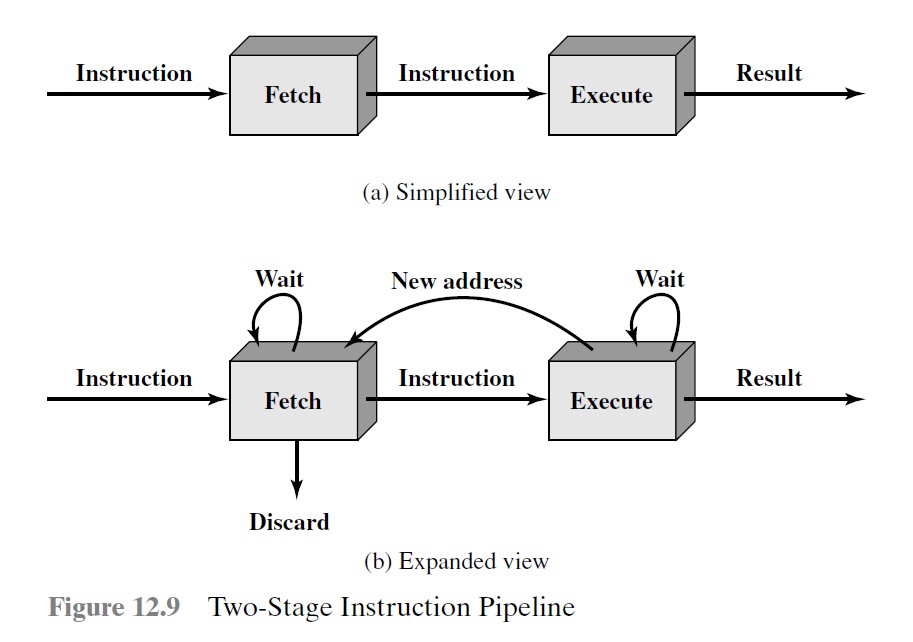
取指和执行
限制:
- 时间分配不均匀
- 主存访问冲突
- 分支指令使得待取的下一条指令的地址是未知的
六阶段
- 取指令(FI)
读下一个预期的指令到缓冲器
- 译码指令(DI)
确定操作码和操作数指定器
- 计算操作数(CO)
计算每个源操作数的有效地址,这可能涉及到偏移、寄存器间接、间接或其他形式的地址计算
- 取操作数(FO)
由存储器取每个操作数。寄存器中的操作数不需要取
- 执行指令(EI)
完成指定的操作。若有指定的目标操作数位置,则将结果写入此位置
- 写操作数(WO)
将结果存入存储器
限制:
- 不是所有指令都包含 6 个阶段 → 假定每条指令都是 6 个阶段
- 主存访问冲突,不是所有的阶段都能并行完成
- 条件转移指令能使若干指令的读取变为无效
- 中断
流水线性能

条指令:
- 阶段流水线:
- 无流水线:
冒险
结构冒险

存储器 → 指令存储器、数据存储器
寄存器 → 上升沿写、下降沿读
数据冒险
Read After Write
add $1, $2, $3xor $4, $1, $2- 插入空操作(软件指令)
- 插入气泡(硬件阻塞)
- 转发
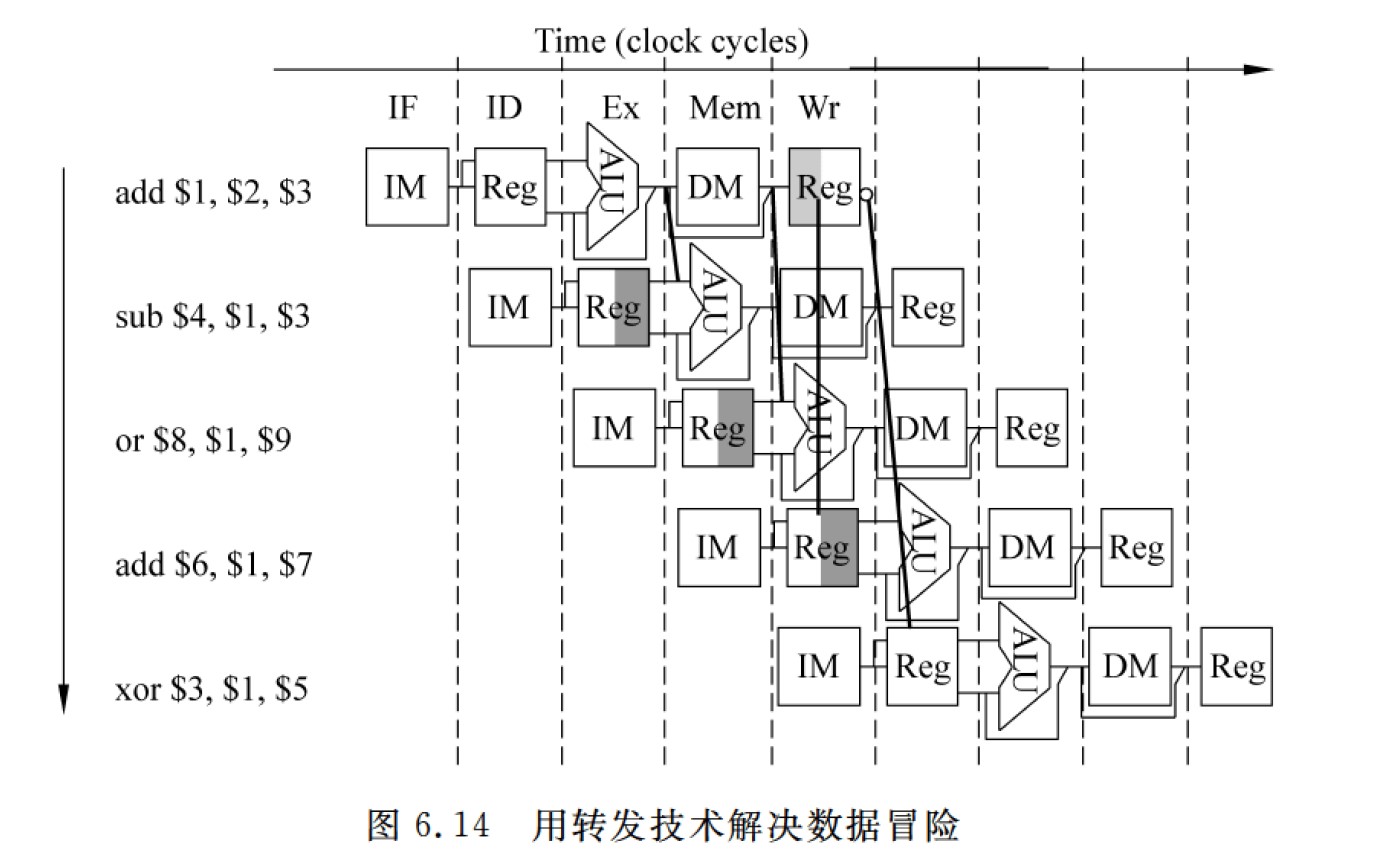
上一条指令的 ALU 输出立即转发到下一条指令的 ALU 输入
Load Use
lw $1, (0)$2xor $4, $1, $2- 插入空操作(软件指令)
- 插入气泡(硬件阻塞)
- 调整指令顺序
控制冒险
指令的执行顺序被更改:
- 转移
- 中断
- 异常
- 调用 / 返回
解决:
- 取多条指令
- 分支预测
- 静态
- 动态:转移处理状态图
控制器
W 12 / 15 / 16
Y 5
- 寄存器
- 用户可见寄存器:常见类型,设计出发点,保存和恢复
- 控制和状态寄存器:常见类型,设计出发点
- 微操作
- 控制器:输入和输出,控制信号
- 控制器实现
- 硬布线实现:控制器输入,控制器逻辑
- 微程序实现
- 基本概念和思路:微程序,微指令
- 微程序控制器:任务,构成,工作流程
用户可见寄存器
- 通用寄存器
- 数据寄存器
- 地址寄存器
- 条件码寄存器 / 标志寄存器
- 部分用户可见
设计出发点
- 通用还是专用
- 数量
- 长度
保存与恢复
- 子程序调用会导致自动保存所有用户可见的寄存器,并在返回时自动取回
- 子程序调用之外保存用户可见寄存器的相关内容是程序员的责任,需要在程序中为此编写专门的指令
控制和状态寄存器
- 程序计数器 -> PC
- 指令寄存器 -> IR
- 存储器地址寄存器 -> MAR
- 存储器缓冲寄存器 -> MBR
- 程序状态字 -> Program status word PSW
- 一个或一组包含状态信息的寄存器,包含条件码加上其他状态信息
设计出发点
- 对操作系统的支持
- 控制信息在寄存器和存储器之间的分配
微操作
数据流的实现
一条机器指令的分解:
- 指令周期
- 子周期
- CPU 寄存器操作(微操作)

取指周期
t1: MAR ← (PC)t2: MBR ← Memory PC ← (PC) + It3: IR ← (MBR)内存读操作要使用 MAR 中的地址
MBR ← Memory 和 IR ← (MBR) 这两个微操作不应出现在同一时间单位里
所用的时间单位应尽可能少
间址周期
t1: MAR ← (IR(Address))t2: MBR ← Memoryt3: IR(Address) ← (MBR(Address))操作数的有效地址在 IR 的地址字段
执行周期
对于不同的操作码,会出现不同的微操作序列
中断周期
t1: MBR ← (PC) MAR ← Save_Addresst2: PC ← Routine_Address Memory ← (MBR)指令周期代码
Instruction Cycle Code, ICC
假设一个 2 位的 ICC 寄存器,明确 CPU 处于指令周期哪个阶段

控制器
基本任务
- 定序
- 执行
输入输出

- 输入
- 指令寄存器
- 标志
- CPU
- ALU
- 时钟
- 来自控制总线的控制信号
- 如中断请求
- 输出
- CPU 内的控制信号
- 用于寄存器之间传送数据
- 用于启动特定的 ALU 功能
- 到控制总线的控制信号
- 到存储器的控制信号
- 到 I/O 模块的控制信号
- CPU 内的控制信号
控制信号
ALU 和寄存器都连接到 CPU 内部总线上
为了数据在该内部总线和各寄存器之间传递,内部总线和寄存器之间有门和控制信号
控制线控制着数据和系统总线(外部)的交换以及 ALU 的操作
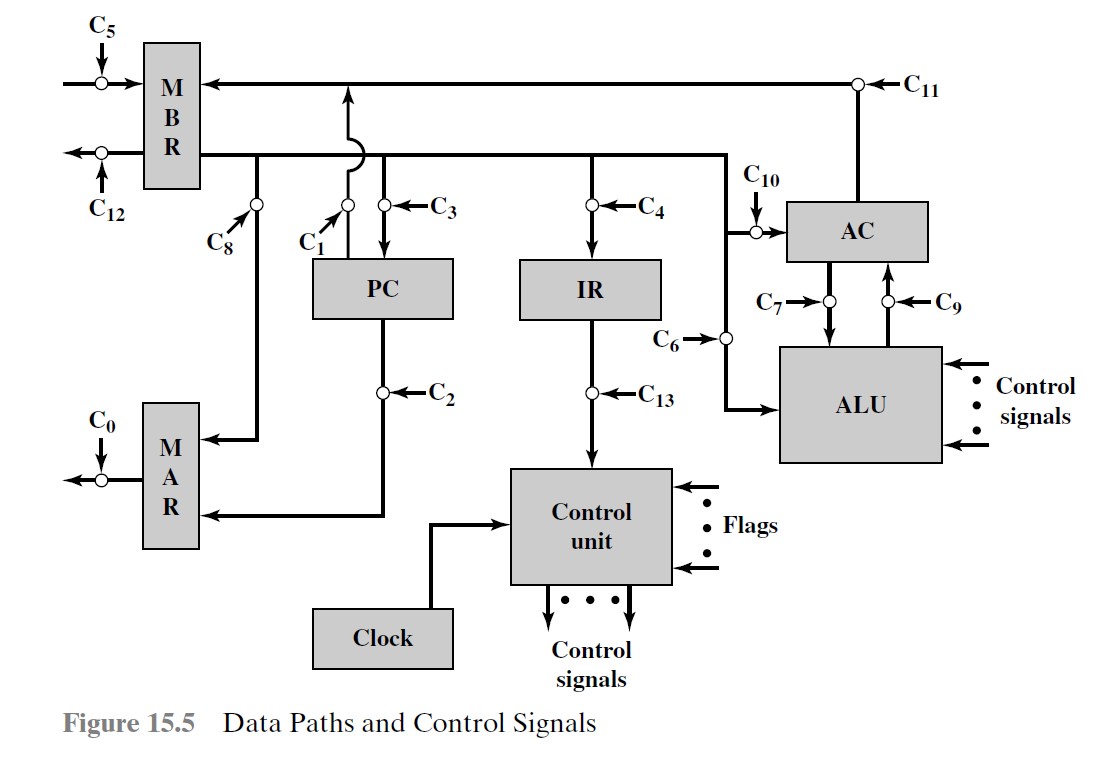
以取指周期为例:
t1: MAR ← (PC)
c2
t2: MBR ← Memory PC ← (PC) + I
C0 CR C5
t3: IR ← (MBR)
C4PC 自增没有在图中体现出来
硬布线实现

为每个输出的控制信号设计一个关于控制器输入的布尔表达式
以上述 为例:
其中 和 指示指令周期哪个阶段, 指示子周期的当前时间
翻译为: 在取指、间接、执行周期(指令 或 )的第二个时间单位有效
微程序实现
构造一个控制字,每位代表一根控制线,将这些控制字串在一起,可以表示控制器需要完成的微操作序列。
由于微操作序列不是固定的,把控制字放入一个存储器单元中,每个字有自己唯一的地址。
整体结构如下:

其中控制存储器如下:

其中最重要的部分是定序逻辑,请自行理解……
输入输出
W 7
Y 8
- 外围设备
- I/O 模块:功能,结构
- I/O 操作技术
- 编程式 I/O
- 中断驱动式 I/O
- 直接存储器存取
- I/O 模块的演变
外围设备
不属于计算机系统
- 人可读设备:适用于与计算机用户通信
- 显示器,打印机,……
- 机器可读设备:适用于与设备通信
- 磁盘,磁带,……
- 通信设备:适用于与远程设备通信
不能把外设直接连接到系统总线上:
- 外设种类繁多,操作方法多种多样
- 外设的数据传送速度一般比存储器或处理器的慢得多
- 某些外设的数据传送速度比存储器或处理器要快
- 外设使用的数据格式和字长度通常与处理器不同
I/O 模块
属于计算机系统
功能
- 处理器通信
- 设备通信
- 数据缓冲
- 控制和定时
- 检错
结构

- 控制线
- CPU → IO
- 发送命令
- IO → CPU
- 仲裁和传递状态信号
- CPU → IO
- 状态和控制寄存器
- 控制寄存器
- CPU → IO
- 具体的控制信息
- 状态寄存器
- IO → CPU
- 当前的状态信息
- 控制寄存器
- 外部设备接口
- 并行接口
- 串行接口
- 由于并行接口要求每次同时传送,当传输速度和总线长度增加时,总线的时钟频率会受到限制,故通常使用串行
- FireWire
- USB

I/O 操作技术

编程式 I/O

- 处理 IO 时间占 CPU 时间的百分比为 100%
- I/O 命令
- I/O 指令
- 编址方式
- 存储器映射式 I/O
- 分离式 I/O
- 编址方式
中断驱动式 I/O

- 从 I/O 模块的角度来看
- I/O 模块接收来自处理器的读命令
- I/O 模块从相关的外设中读入数据
- 一旦数据进入 I/O 模块的数据寄存器后,该模块通过控制总线给处理器发送中断信号
- I/O 模块等待直到处理器请求该数据时为止
- 当处理器有数据请求时,I/O 模块把数据传送到数据总线上,并准备另一个 I/O 操作
- 从处理器的角度来看
- 处理器发送一个读命令
- 处理器离开去做其它的事情,并在每个指令周期结束时检查中断
- 当来自 I/O 模块的中断出现时,处理器保存当前程序的现场
- 处理器从 I/O 模块读取数据字并保存到主存中
- 处理器恢复刚才正在运行的程序的现场,并继续运行原来的程序
- 中断允许和中断禁止
- 在保存和恢复时禁止中断
- 在中断处理过程中允许中断允许
- 响应优先级和处理优先级
- 响应优先级 - 最先抢到位置
- 处理优先级 - 最后占有位置
- 掩码字 / 屏蔽字 - 行屏蔽列
- 详见袁妈教材
- 设计问题
- 设备识别与优先级
- 一些技术
- 多条中断线
- 软件轮询
- 菊花链
- 独立请求
直接存储器存取

- DMA 模块

- 流程
- 处理器通过发送以下信息向 DMA 模块发出命令:读/写、I/O 设备地址、内存中的起始位置、字数
- 处理器继续进行其他工作
- DMA 模块将全部数据块,每次一个字,直接将数据传输到存储器或从存储器读出,而无需经过处理器
- 当传输完成时,DMA 模块向处理器发送一个中断信号
- 问题
- DMA 和 CPU 都会访问内存,会发生冲突
- DMA 优先
- 设备占用总线
- DMA 和 CPU 都会访问内存,会发生冲突
- DMA 内存访问
- CPU 停止法
- 周期窃取
- IO 周期大于存储周期
- 交替分时访问
- CPU 周期小于存储周期
- DMA 配置机制
I/O 模块的演变
- CPU 直接控制外设
- 增加控制器或 I/O 模块,CPU 使用编程式 I/O,将 CPU 与外围设备的细节分离
- 采用中断,CPU 无需花费时间等待外围设备就绪
- I/O 模块可通过 DMA 直接存取存储器,无需 CPU 负责存储器和 I/O 模块之间的数据传递
- I/O 通道:I/O 模块有自己的处理器,带有专门为 I/O 操作定制的指令集
- CPU 指示 I/O 通道执行存储器中的 I/O 指令,只有在执行完成后才会中断 CPU
- I/O 处理器:I/O 模块有一个局部存储器,I/O 模块成为一个自治的计算机,常用于与交互式终端进行通信
- 只需最少的 CPU 参与即可控制大量 I/O 设备